Flipping Against All Odds: Reducing LLM Coin Flip Bias via Verbalized Rejection Sampling

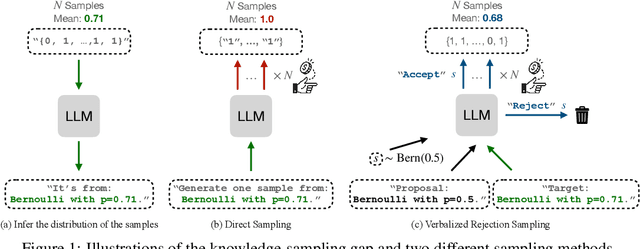
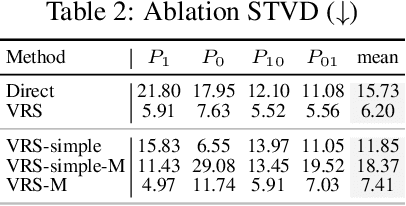
Large language models (LLMs) can often accurately describe probability distributions using natural language, yet they still struggle to generate faithful samples from them. This mismatch limits their use in tasks requiring reliable stochasticity, such as Monte Carlo methods, agent-based simulations, and randomized decision-making. We investigate this gap between knowledge and sampling in the context of Bernoulli distributions. We introduce Verbalized Rejection Sampling (VRS), a natural-language adaptation of classical rejection sampling that prompts the LLM to reason about and accept or reject proposed samples. Despite relying on the same Bernoulli mechanism internally, VRS substantially reduces sampling bias across models. We provide theoretical analysis showing that, under mild assumptions, VRS improves over direct sampling, with gains attributable to both the algorithm and prompt design. More broadly, our results show how classical probabilistic tools can be verbalized and embedded into LLM workflows to improve reliability, without requiring access to model internals or heavy prompt engineering.

Balancing Molecular Information and Empirical Data in the Prediction of Physico-Chemical Properties

Predicting the physico-chemical properties of pure substances and mixtures is a central task in thermodynamics. Established prediction methods range from fully physics-based ab-initio calculations, which are only feasible for very simple systems, over descriptor-based methods that use some information on the molecules to be modeled together with fitted model parameters (e.g., quantitative-structure-property relationship methods or classical group contribution methods), to representation-learning methods, which may, in extreme cases, completely ignore molecular descriptors and extrapolate only from existing data on the property to be modeled (e.g., matrix completion methods). In this work, we propose a general method for combining molecular descriptors with representation learning using the so-called expectation maximization algorithm from the probabilistic machine learning literature, which uses uncertainty estimates to trade off between the two approaches. The proposed hybrid model exploits chemical structure information using graph neural networks, but it automatically detects cases where structure-based predictions are unreliable, in which case it corrects them by representation-learning based predictions that can better specialize to unusual cases. The effectiveness of the proposed method is demonstrated using the prediction of activity coefficients in binary mixtures as an example. The results are compelling, as the method significantly improves predictive accuracy over the current state of the art, showcasing its potential to advance the prediction of physico-chemical properties in general.

Upgrading VAE Training With Unlimited Data Plans Provided by Diffusion Models

Variational autoencoders (VAEs) are popular models for representation learning but their encoders are susceptible to overfitting (Cremer et al., 2018) because they are trained on a finite training set instead of the true (continuous) data distribution $p_{\mathrm{data}}(\mathbf{x})$. Diffusion models, on the other hand, avoid this issue by keeping the encoder fixed. This makes their representations less interpretable, but it simplifies training, enabling accurate and continuous approximations of $p_{\mathrm{data}}(\mathbf{x})$. In this paper, we show that overfitting encoders in VAEs can be effectively mitigated by training on samples from a pre-trained diffusion model. These results are somewhat unexpected as recent findings (Alemohammad et al., 2023; Shumailov et al., 2023) observe a decay in generative performance when models are trained on data generated by another generative model. We analyze generalization performance, amortization gap, and robustness of VAEs trained with our proposed method on three different data sets. We find improvements in all metrics compared to both normal training and conventional data augmentation methods, and we show that a modest amount of samples from the diffusion model suffices to obtain these gains.

Resampling Gradients Vanish in Differentiable Sequential Monte Carlo Samplers

Annealed Importance Sampling (AIS) moves particles along a Markov chain from a tractable initial distribution to an intractable target distribution. The recently proposed Differentiable AIS (DAIS) (Geffner and Domke, 2021; Zhang et al., 2021) enables efficient optimization of the transition kernels of AIS and of the distributions. However, we observe a low effective sample size in DAIS, indicating degenerate distributions. We thus propose to extend DAIS by a resampling step inspired by Sequential Monte Carlo. Surprisingly, we find empirically-and can explain theoretically-that it is not necessary to differentiate through the resampling step which avoids gradient variance issues observed in similar approaches for Particle Filters (Maddison et al., 2017; Naesseth et al., 2018; Le et al., 2018).

ProbNum: Probabilistic Numerics in Python

Probabilistic numerical methods (PNMs) solve numerical problems via probabilistic inference. They have been developed for linear algebra, optimization, integration and differential equation simulation. PNMs naturally incorporate prior information about a problem and quantify uncertainty due to finite computational resources as well as stochastic input. In this paper, we present ProbNum: a Python library providing state-of-the-art probabilistic numerical solvers. ProbNum enables custom composition of PNMs for specific problem classes via a modular design as well as wrappers for off-the-shelf use. Tutorials, documentation, developer guides and benchmarks are available online at www.probnum.org.