Active learning for affinity prediction of antibodies

The primary objective of most lead optimization campaigns is to enhance the binding affinity of ligands. For large molecules such as antibodies, identifying mutations that enhance antibody affinity is particularly challenging due to the combinatorial explosion of potential mutations. When the structure of the antibody-antigen complex is available, relative binding free energy (RBFE) methods can offer valuable insights into how different mutations will impact the potency and selectivity of a drug candidate, thereby reducing the reliance on costly and time-consuming wet-lab experiments. However, accurately simulating the physics of large molecules is computationally intensive. We present an active learning framework that iteratively proposes promising sequences for simulators to evaluate, thereby accelerating the search for improved binders. We explore different modeling approaches to identify the most effective surrogate model for this task, and evaluate our framework both using pre-computed pools of data and in a realistic full-loop setting.

Spatiotemporal modeling of European paleoclimate using doubly sparse Gaussian processes

Paleoclimatology -- the study of past climate -- is relevant beyond climate science itself, such as in archaeology and anthropology for understanding past human dispersal. Information about the Earth's paleoclimate comes from simulations of physical and biogeochemical processes and from proxy records found in naturally occurring archives. Climate-field reconstructions (CFRs) combine these data into a statistical spatial or spatiotemporal model. To date, there exists no consensus spatiotemporal paleoclimate model that is continuous in space and time, produces predictions with uncertainty, and can include data from various sources. A Gaussian process (GP) model would have these desired properties; however, GPs scale unfavorably with data of the magnitude typical for building CFRs. We propose to build on recent advances in sparse spatiotemporal GPs that reduce the computational burden by combining variational methods based on inducing variables with the state-space formulation of GPs. We successfully employ such a doubly sparse GP to construct a probabilistic model of European paleoclimate from the Last Glacial Maximum (LGM) to the mid-Holocene (MH) that synthesizes paleoclimate simulations and fossilized pollen proxy data.

ProbNum: Probabilistic Numerics in Python

Probabilistic numerical methods (PNMs) solve numerical problems via probabilistic inference. They have been developed for linear algebra, optimization, integration and differential equation simulation. PNMs naturally incorporate prior information about a problem and quantify uncertainty due to finite computational resources as well as stochastic input. In this paper, we present ProbNum: a Python library providing state-of-the-art probabilistic numerical solvers. ProbNum enables custom composition of PNMs for specific problem classes via a modular design as well as wrappers for off-the-shelf use. Tutorials, documentation, developer guides and benchmarks are available online at www.probnum.org.

High-Dimensional Gaussian Process Inference with Derivatives

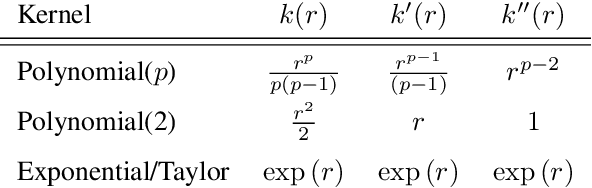
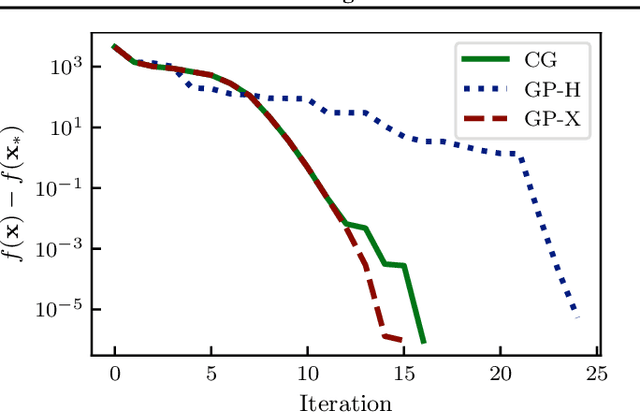
Although it is widely known that Gaussian processes can be conditioned on observations of the gradient, this functionality is of limited use due to the prohibitive computational cost of $\mathcal{O}(N^3 D^3)$ in data points $N$ and dimension $D$. The dilemma of gradient observations is that a single one of them comes at the same cost as $D$ independent function evaluations, so the latter are often preferred. Careful scrutiny reveals, however, that derivative observations give rise to highly structured kernel Gram matrices for very general classes of kernels (inter alia, stationary kernels). We show that in the low-data regime $N<D$, the Gram matrix can be decomposed in a manner that reduces the cost of inference to $\mathcal{O}(N^2D + (N^2)^3)$ (i.e., linear in the number of dimensions) and, in special cases, to $\mathcal{O}(N^2D + N^3)$. This reduction in complexity opens up new use-cases for inference with gradients especially in the high-dimensional regime, where the information-to-cost ratio of gradient observations significantly increases. We demonstrate this potential in a variety of tasks relevant for machine learning, such as optimization and Hamiltonian Monte Carlo with predictive gradients.

Bayesian Quadrature on Riemannian Data Manifolds

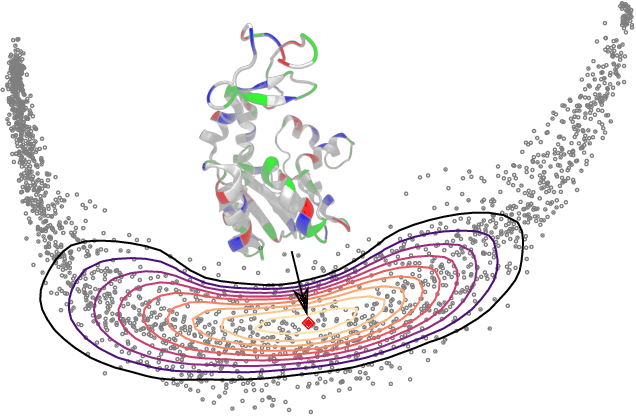
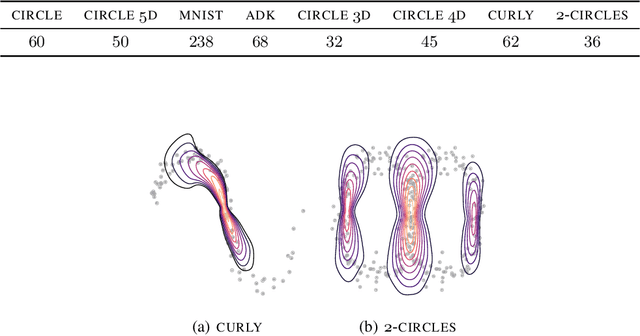
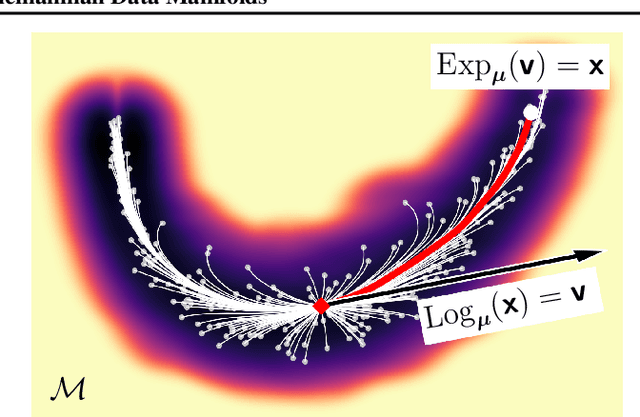
Riemannian manifolds provide a principled way to model nonlinear geometric structure inherent in data. A Riemannian metric on said manifolds determines geometry-aware shortest paths and provides the means to define statistical models accordingly. However, these operations are typically computationally demanding. To ease this computational burden, we advocate probabilistic numerical methods for Riemannian statistics. In particular, we focus on Bayesian quadrature (BQ) to numerically compute integrals over normal laws on Riemannian manifolds learned from data. In this task, each function evaluation relies on the solution of an expensive initial value problem. We show that by leveraging both prior knowledge and an active exploration scheme, BQ significantly reduces the number of required evaluations and thus outperforms Monte Carlo methods on a wide range of integration problems. As a concrete application, we highlight the merits of adopting Riemannian geometry with our proposed framework on a nonlinear dataset from molecular dynamics.

Integrals over Gaussians under Linear Domain Constraints

Integrals of linearly constrained multivariate Gaussian densities are a frequent problem in machine learning and statistics, arising in tasks like generalized linear models and Bayesian optimization. Yet they are notoriously hard to compute, and to further complicate matters, the numerical values of such integrals may be very small. We present an efficient black-box algorithm that exploits geometry for the estimation of integrals over a small, truncated Gaussian volume, and to simulate therefrom. Our algorithm uses the Holmes-Diaconis-Ross (HDR) method combined with an analytic version of elliptical slice sampling (ESS). Adapted to the linear setting, ESS allows for efficient, rejection-free sampling, because intersections of ellipses and domain boundaries have closed-form solutions. The key idea of HDR is to decompose the integral into easier-to-compute conditional probabilities by using a sequence of nested domains. Remarkably, it allows for direct computation of the logarithm of the integral value and thus enables the computation of extremely small probability masses. We demonstrate the effectiveness of our tailored combination of HDR and ESS on high-dimensional integrals and on entropy search for Bayesian optimization.

Active Multi-Information Source Bayesian Quadrature

Bayesian quadrature (BQ) is a sample-efficient probabilistic numerical method to solve integrals of expensive-to-evaluate black-box functions, yet so far,active BQ learning schemes focus merely on the integrand itself as information source, and do not allow for information transfer from cheaper, related functions. Here, we set the scene for active learning in BQ when multiple related information sources of variable cost (in input and source) are accessible. This setting arises for example when evaluating the integrand requires a complex simulation to be run that can be approximated by simulating at lower levels of sophistication and at lesser expense. We construct meaningful cost-sensitive multi-source acquisition rates as an extension to common utility functions from vanilla BQ (VBQ),and discuss pitfalls that arise from blindly generalizing. Furthermore, we show that the VBQ acquisition policy is a corner-case of all considered cost-sensitive acquisition schemes, which collapse onto one single de-generate policy in the case of one source and constant cost. In proof-of-concept experiments we scrutinize the behavior of our generalized acquisition functions. On an epidemiological model, we demonstrate that active multi-source BQ (AMS-BQ) allocates budget more efficiently than VBQ for learning the integral to a good accuracy.