Extended Neural Contractive Dynamical Systems: On Multiple Tasks and Riemannian Safety Regions

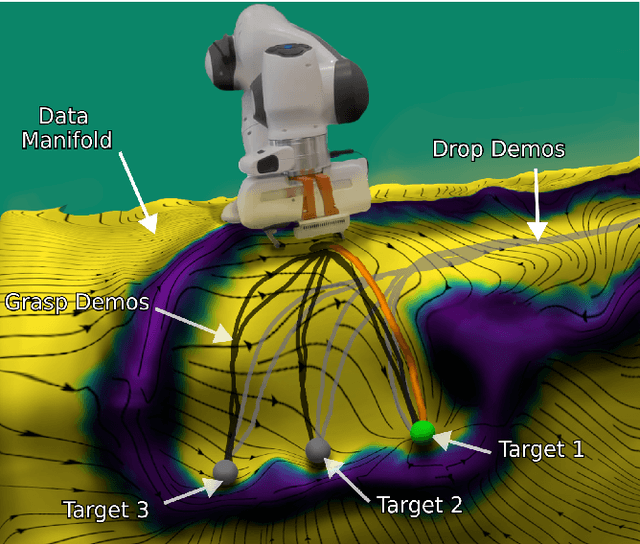
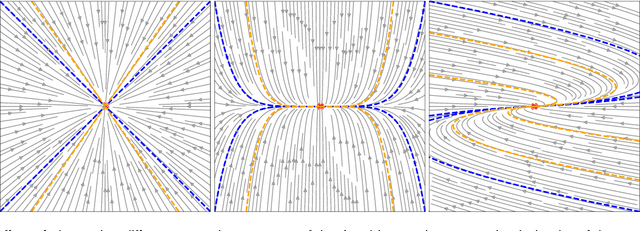
Stability guarantees are crucial when ensuring that a fully autonomous robot does not take undesirable or potentially harmful actions. We recently proposed the Neural Contractive Dynamical Systems (NCDS), which is a neural network architecture that guarantees contractive stability. With this, learning-from-demonstrations approaches can trivially provide stability guarantees. However, our early work left several unanswered questions, which we here address. Beyond providing an in-depth explanation of NCDS, this paper extends the framework with more careful regularization, a conditional variant of the framework for handling multiple tasks, and an uncertainty-driven approach to latent obstacle avoidance. Experiments verify that the developed system has the flexibility of ordinary neural networks while providing the stability guarantees needed for autonomous robotics.

Counterfactual Explanations via Riemannian Latent Space Traversal

The adoption of increasingly complex deep models has fueled an urgent need for insight into how these models make predictions. Counterfactual explanations form a powerful tool for providing actionable explanations to practitioners. Previously, counterfactual explanation methods have been designed by traversing the latent space of generative models. Yet, these latent spaces are usually greatly simplified, with most of the data distribution complexity contained in the decoder rather than the latent embedding. Thus, traversing the latent space naively without taking the nonlinear decoder into account can lead to unnatural counterfactual trajectories. We introduce counterfactual explanations obtained using a Riemannian metric pulled back via the decoder and the classifier under scrutiny. This metric encodes information about the complex geometric structure of the data and the learned representation, enabling us to obtain robust counterfactual trajectories with high fidelity, as demonstrated by our experiments in real-world tabular datasets.

Neural Contractive Dynamical Systems

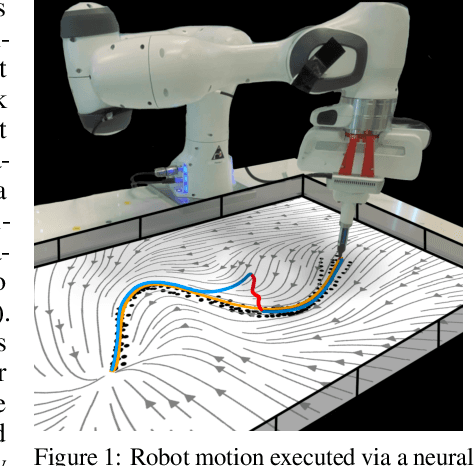
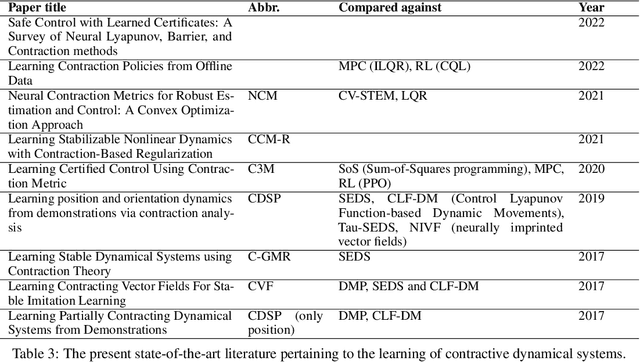
Stability guarantees are crucial when ensuring a fully autonomous robot does not take undesirable or potentially harmful actions. Unfortunately, global stability guarantees are hard to provide in dynamical systems learned from data, especially when the learned dynamics are governed by neural networks. We propose a novel methodology to learn neural contractive dynamical systems, where our neural architecture ensures contraction, and hence, global stability. To efficiently scale the method to high-dimensional dynamical systems, we develop a variant of the variational autoencoder that learns dynamics in a low-dimensional latent representation space while retaining contractive stability after decoding. We further extend our approach to learning contractive systems on the Lie group of rotations to account for full-pose end-effector dynamic motions. The result is the first highly flexible learning architecture that provides contractive stability guarantees with capability to perform obstacle avoidance. Empirically, we demonstrate that our approach encodes the desired dynamics more accurately than the current state-of-the-art, which provides less strong stability guarantees.

On the curvature of the loss landscape

One of the main challenges in modern deep learning is to understand why such over-parameterized models perform so well when trained on finite data. A way to analyze this generalization concept is through the properties of the associated loss landscape. In this work, we consider the loss landscape as an embedded Riemannian manifold and show that the differential geometric properties of the manifold can be used when analyzing the generalization abilities of a deep net. In particular, we focus on the scalar curvature, which can be computed analytically for our manifold, and show connections to several settings that potentially imply generalization.

Riemannian Laplace approximations for Bayesian neural networks

Bayesian neural networks often approximate the weight-posterior with a Gaussian distribution. However, practical posteriors are often, even locally, highly non-Gaussian, and empirical performance deteriorates. We propose a simple parametric approximate posterior that adapts to the shape of the true posterior through a Riemannian metric that is determined by the log-posterior gradient. We develop a Riemannian Laplace approximation where samples naturally fall into weight-regions with low negative log-posterior. We show that these samples can be drawn by solving a system of ordinary differential equations, which can be done efficiently by leveraging the structure of the Riemannian metric and automatic differentiation. Empirically, we demonstrate that our approach consistently improves over the conventional Laplace approximation across tasks. We further show that, unlike the conventional Laplace approximation, our method is not overly sensitive to the choice of prior, which alleviates a practical pitfall of current approaches.

Reactive Motion Generation on Learned Riemannian Manifolds

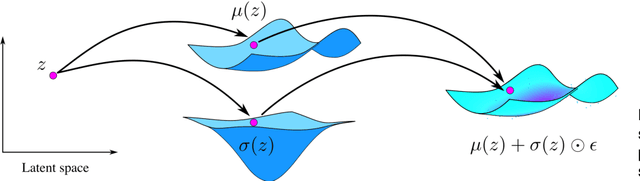
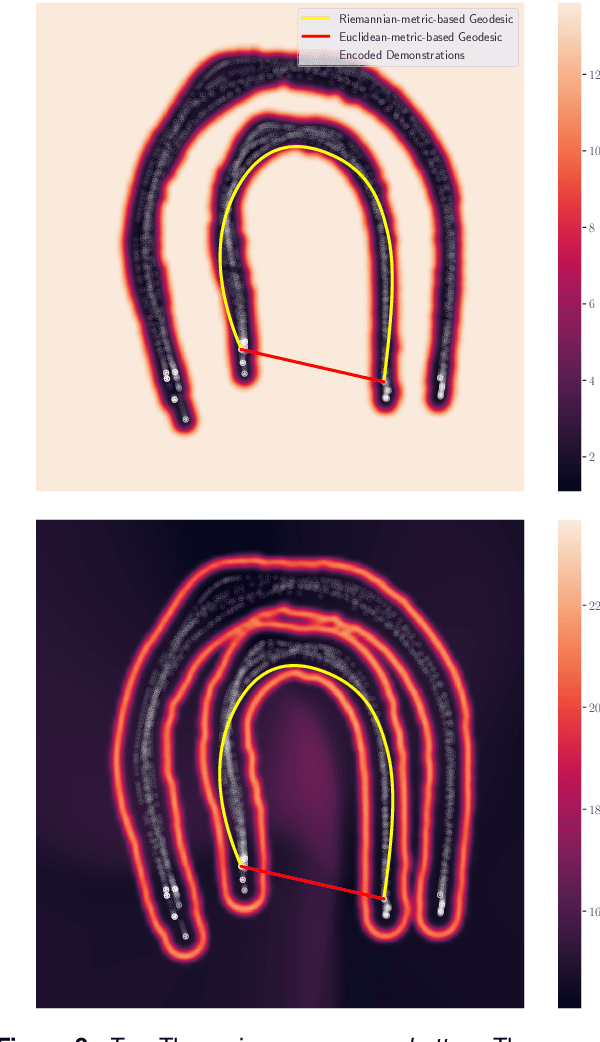
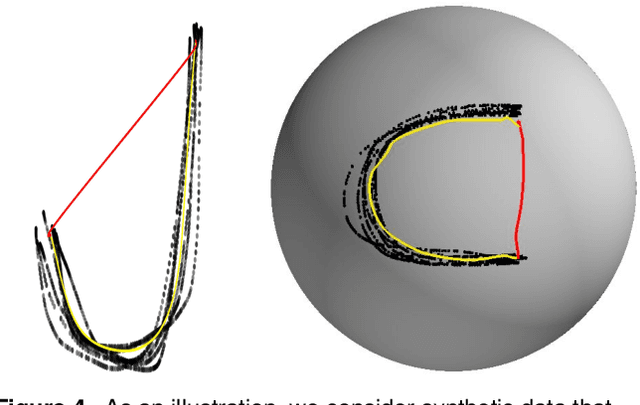
In recent decades, advancements in motion learning have enabled robots to acquire new skills and adapt to unseen conditions in both structured and unstructured environments. In practice, motion learning methods capture relevant patterns and adjust them to new conditions such as dynamic obstacle avoidance or variable targets. In this paper, we investigate the robot motion learning paradigm from a Riemannian manifold perspective. We argue that Riemannian manifolds may be learned via human demonstrations in which geodesics are natural motion skills. The geodesics are generated using a learned Riemannian metric produced by our novel variational autoencoder (VAE), which is especially intended to recover full-pose end-effector states and joint space configurations. In addition, we propose a technique for facilitating on-the-fly end-effector/multiple-limb obstacle avoidance by reshaping the learned manifold using an obstacle-aware ambient metric. The motion generated using these geodesics may naturally result in multiple-solution tasks that have not been explicitly demonstrated previously. We extensively tested our approach in task space and joint space scenarios using a 7-DoF robotic manipulator. We demonstrate that our method is capable of learning and generating motion skills based on complicated motion patterns demonstrated by a human operator. Additionally, we assess several obstacle avoidance strategies and generate trajectories in multiple-mode settings.

On the Impact of Stable Ranks in Deep Nets

A recent line of work has established intriguing connections between the generalization/compression properties of a deep neural network (DNN) model and the so-called layer weights' stable ranks. Intuitively, the latter are indicators of the effective number of parameters in the net. In this work, we address some natural questions regarding the space of DNNs conditioned on the layers' stable rank, where we study feed-forward dynamics, initialization, training and expressivity. To this end, we first propose a random DNN model with a new sampling scheme based on stable rank. Then, we show how feed-forward maps are affected by the constraint and how training evolves in the overparametrized regime (via Neural Tangent Kernels). Our results imply that stable ranks appear layerwise essentially as linear factors whose effect accumulates exponentially depthwise. Moreover, we provide empirical analysis suggesting that stable rank initialization alone can lead to convergence speed ups.

Pulling back information geometry

Latent space geometry has shown itself to provide a rich and rigorous framework for interacting with the latent variables of deep generative models. The existing theory, however, relies on the decoder being a Gaussian distribution as its simple reparametrization allows us to interpret the generating process as a random projection of a deterministic manifold. Consequently, this approach breaks down when applied to decoders that are not as easily reparametrized. We here propose to use the Fisher-Rao metric associated with the space of decoder distributions as a reference metric, which we pull back to the latent space. We show that we can achieve meaningful latent geometries for a wide range of decoder distributions for which the previous theory was not applicable, opening the door to `black box' latent geometries.

Learning Riemannian Manifolds for Geodesic Motion Skills

For robots to work alongside humans and perform in unstructured environments, they must learn new motion skills and adapt them to unseen situations on the fly. This demands learning models that capture relevant motion patterns, while offering enough flexibility to adapt the encoded skills to new requirements, such as dynamic obstacle avoidance. We introduce a Riemannian manifold perspective on this problem, and propose to learn a Riemannian manifold from human demonstrations on which geodesics are natural motion skills. We realize this with a variational autoencoder (VAE) over the space of position and orientations of the robot end-effector. Geodesic motion skills let a robot plan movements from and to arbitrary points on the data manifold. They also provide a straightforward method to avoid obstacles by redefining the ambient metric in an online fashion. Moreover, geodesics naturally exploit the manifold resulting from multiple--mode tasks to design motions that were not explicitly demonstrated previously. We test our learning framework using a 7-DoF robotic manipulator, where the robot satisfactorily learns and reproduces realistic skills featuring elaborated motion patterns, avoids previously unseen obstacles, and generates novel movements in multiple-mode settings.

A prior-based approximate latent Riemannian metric

Stochastic generative models enable us to capture the geometric structure of a data manifold lying in a high dimensional space through a Riemannian metric in the latent space. However, its practical use is rather limited mainly due to inevitable complexity. In this work we propose a surrogate conformal Riemannian metric in the latent space of a generative model that is simple, efficient and robust. This metric is based on a learnable prior that we propose to learn using a basic energy-based model. We theoretically analyze the behavior of the proposed metric and show that it is sensible to use in practice. We demonstrate experimentally the efficiency and robustness, as well as the behavior of the new approximate metric. Also, we show the applicability of the proposed methodology for data analysis in the life sciences.