On the Impact of Stable Ranks in Deep Nets
Paper and Code
Oct 05, 2021
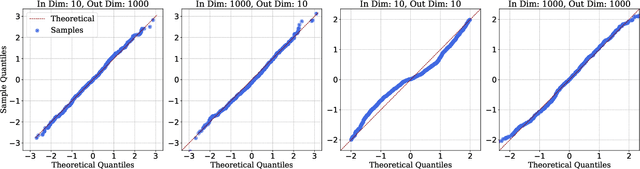
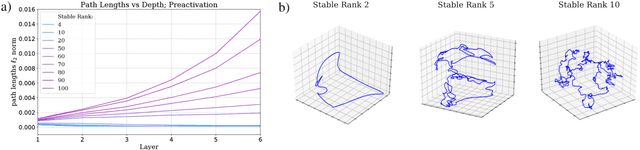
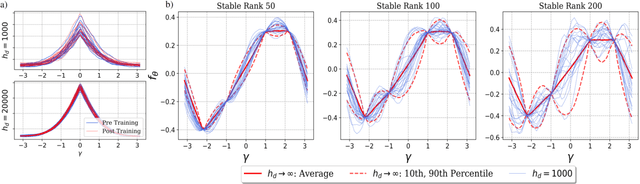
A recent line of work has established intriguing connections between the generalization/compression properties of a deep neural network (DNN) model and the so-called layer weights' stable ranks. Intuitively, the latter are indicators of the effective number of parameters in the net. In this work, we address some natural questions regarding the space of DNNs conditioned on the layers' stable rank, where we study feed-forward dynamics, initialization, training and expressivity. To this end, we first propose a random DNN model with a new sampling scheme based on stable rank. Then, we show how feed-forward maps are affected by the constraint and how training evolves in the overparametrized regime (via Neural Tangent Kernels). Our results imply that stable ranks appear layerwise essentially as linear factors whose effect accumulates exponentially depthwise. Moreover, we provide empirical analysis suggesting that stable rank initialization alone can lead to convergence speed ups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge