A Causal Discovery Approach To Learn How Urban Form Shapes Sustainable Mobility Across Continents

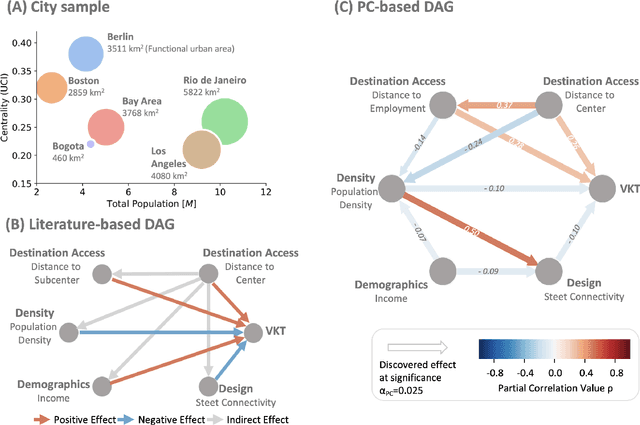
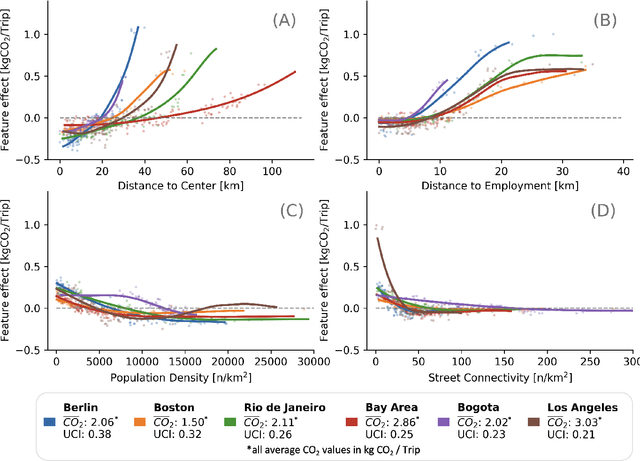
Global sustainability requires low-carbon urban transport systems, shaped by adequate infrastructure, deployment of low-carbon transport modes and shifts in travel behavior. To adequately implement alterations in infrastructure, it's essential to grasp the location-specific cause-and-effect mechanisms that the constructed environment has on travel. Yet, current research falls short in representing causal relationships between the 6D urban form variables and travel, generalizing across different regions, and modeling urban form effects at high spatial resolution. Here, we address all three gaps by utilizing a causal discovery and an explainable machine learning framework to detect urban form effects on intra-city travel based on high-resolution mobility data of six cities across three continents. We show that both distance to city center, demographics and density indirectly affect other urban form features. By considering the causal relationships, we find that location-specific influences align across cities, yet vary in magnitude. In addition, the spread of the city and the coverage of jobs across the city are the strongest determinants of travel-related emissions, highlighting the benefits of compact development and associated benefits. Differences in urban form effects across the cities call for a more holistic definition of 6D measures. Our work is a starting point for location-specific analysis of urban form effects on mobility behavior using causal discovery approaches, which is highly relevant for city planners and municipalities across continents.

On the Impact of Stable Ranks in Deep Nets

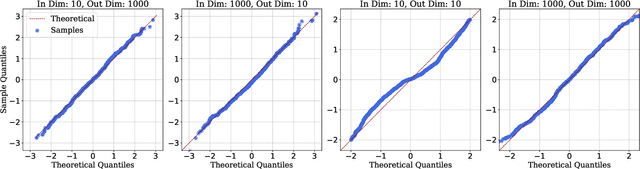
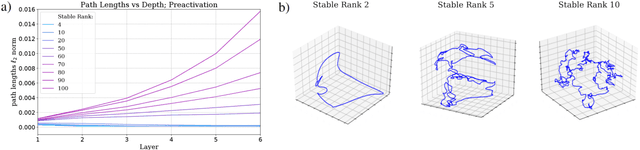
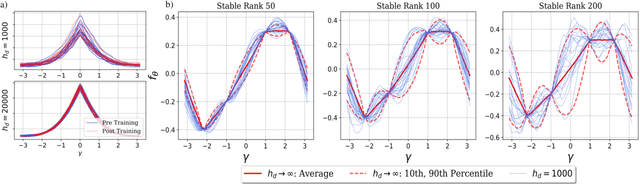
A recent line of work has established intriguing connections between the generalization/compression properties of a deep neural network (DNN) model and the so-called layer weights' stable ranks. Intuitively, the latter are indicators of the effective number of parameters in the net. In this work, we address some natural questions regarding the space of DNNs conditioned on the layers' stable rank, where we study feed-forward dynamics, initialization, training and expressivity. To this end, we first propose a random DNN model with a new sampling scheme based on stable rank. Then, we show how feed-forward maps are affected by the constraint and how training evolves in the overparametrized regime (via Neural Tangent Kernels). Our results imply that stable ranks appear layerwise essentially as linear factors whose effect accumulates exponentially depthwise. Moreover, we provide empirical analysis suggesting that stable rank initialization alone can lead to convergence speed ups.

On the effects of biased quantum random numbers on the initialization of artificial neural networks

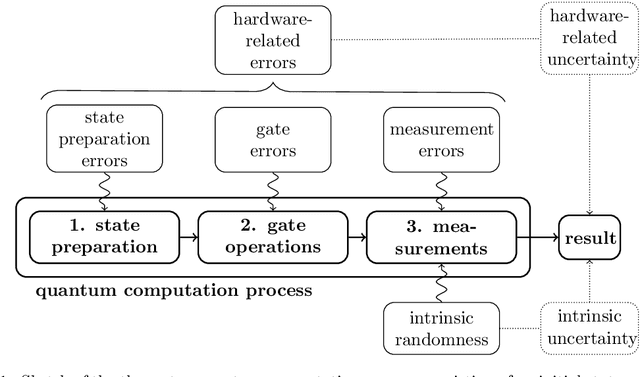
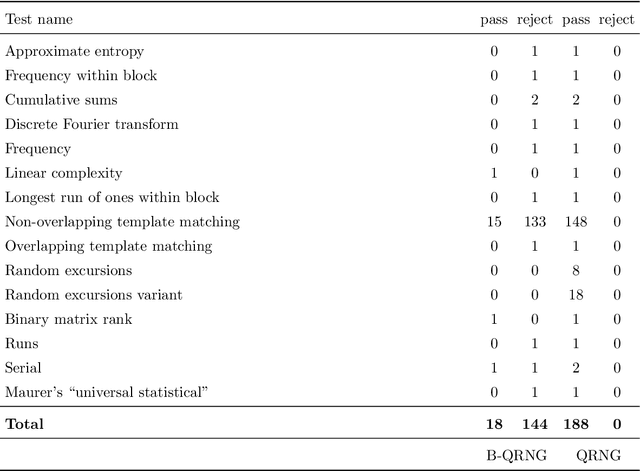
Recent advances in practical quantum computing have led to a variety of cloud-based quantum computing platforms that allow researchers to evaluate their algorithms on noisy intermediate-scale quantum (NISQ) devices. A common property of quantum computers is that they exhibit instances of true randomness as opposed to pseudo-randomness obtained from classical systems. Investigating the effects of such true quantum randomness in the context of machine learning is appealing, and recent results vaguely suggest that benefits can indeed be achieved from the use of quantum random numbers. To shed some more light on this topic, we empirically study the effects of hardware-biased quantum random numbers on the initialization of artificial neural network weights in numerical experiments. We find no statistically significant difference in comparison with unbiased quantum random numbers as well as biased and unbiased random numbers from a classical pseudo-random number generator. The quantum random numbers for our experiments are obtained from real quantum hardware.

Heating up decision boundaries: isocapacitory saturation, adversarial scenarios and generalization bounds

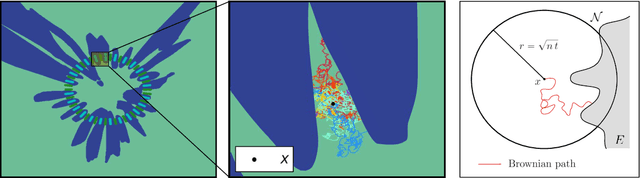
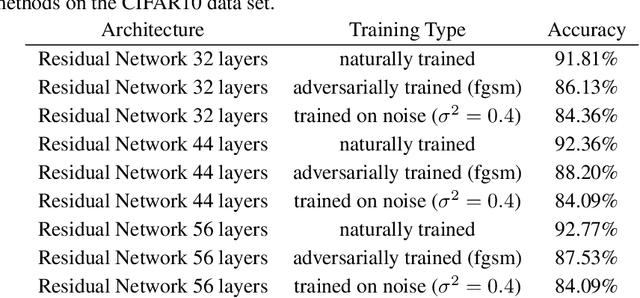
In the present work we study classifiers' decision boundaries via Brownian motion processes in ambient data space and associated probabilistic techniques. Intuitively, our ideas correspond to placing a heat source at the decision boundary and observing how effectively the sample points warm up. We are largely motivated by the search for a soft measure that sheds further light on the decision boundary's geometry. En route, we bridge aspects of potential theory and geometric analysis (Mazya, 2011, Grigoryan-Saloff-Coste, 2002) with active fields of ML research such as adversarial examples and generalization bounds. First, we focus on the geometric behavior of decision boundaries in the light of adversarial attack/defense mechanisms. Experimentally, we observe a certain capacitory trend over different adversarial defense strategies: decision boundaries locally become flatter as measured by isoperimetric inequalities (Ford et al, 2019); however, our more sensitive heat-diffusion metrics extend this analysis and further reveal that some non-trivial geometry invisible to plain distance-based methods is still preserved. Intuitively, we provide evidence that the decision boundaries nevertheless retain many persistent "wiggly and fuzzy" regions on a finer scale. Second, we show how Brownian hitting probabilities translate to soft generalization bounds which are in turn connected to compression and noise stability (Arora et al, 2018), and these bounds are significantly stronger if the decision boundary has controlled geometric features.