On the Impact of Stable Ranks in Deep Nets

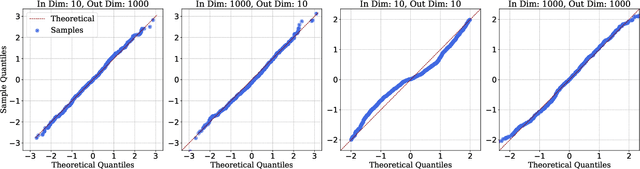
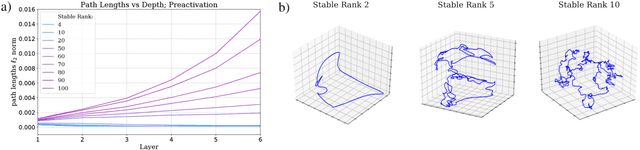
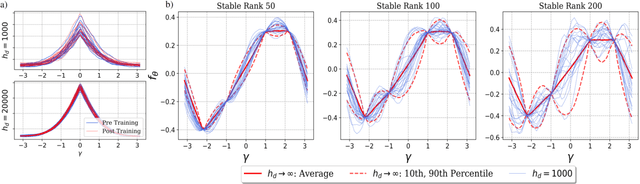
A recent line of work has established intriguing connections between the generalization/compression properties of a deep neural network (DNN) model and the so-called layer weights' stable ranks. Intuitively, the latter are indicators of the effective number of parameters in the net. In this work, we address some natural questions regarding the space of DNNs conditioned on the layers' stable rank, where we study feed-forward dynamics, initialization, training and expressivity. To this end, we first propose a random DNN model with a new sampling scheme based on stable rank. Then, we show how feed-forward maps are affected by the constraint and how training evolves in the overparametrized regime (via Neural Tangent Kernels). Our results imply that stable ranks appear layerwise essentially as linear factors whose effect accumulates exponentially depthwise. Moreover, we provide empirical analysis suggesting that stable rank initialization alone can lead to convergence speed ups.

Heating up decision boundaries: isocapacitory saturation, adversarial scenarios and generalization bounds

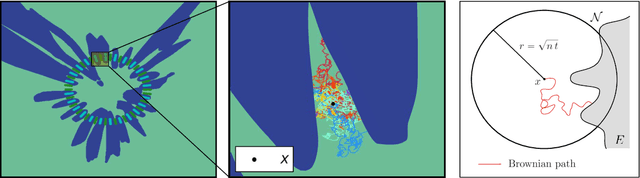
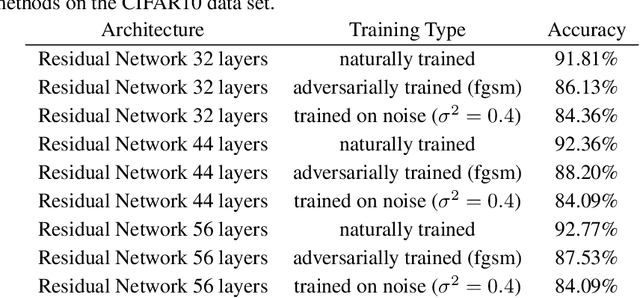
In the present work we study classifiers' decision boundaries via Brownian motion processes in ambient data space and associated probabilistic techniques. Intuitively, our ideas correspond to placing a heat source at the decision boundary and observing how effectively the sample points warm up. We are largely motivated by the search for a soft measure that sheds further light on the decision boundary's geometry. En route, we bridge aspects of potential theory and geometric analysis (Mazya, 2011, Grigoryan-Saloff-Coste, 2002) with active fields of ML research such as adversarial examples and generalization bounds. First, we focus on the geometric behavior of decision boundaries in the light of adversarial attack/defense mechanisms. Experimentally, we observe a certain capacitory trend over different adversarial defense strategies: decision boundaries locally become flatter as measured by isoperimetric inequalities (Ford et al, 2019); however, our more sensitive heat-diffusion metrics extend this analysis and further reveal that some non-trivial geometry invisible to plain distance-based methods is still preserved. Intuitively, we provide evidence that the decision boundaries nevertheless retain many persistent "wiggly and fuzzy" regions on a finer scale. Second, we show how Brownian hitting probabilities translate to soft generalization bounds which are in turn connected to compression and noise stability (Arora et al, 2018), and these bounds are significantly stronger if the decision boundary has controlled geometric features.