Quantum Adiabatic Generation of Human-Like Passwords

Generative Artificial Intelligence (GenAI) for Natural Language Processing (NLP) is the predominant AI technology to date. An important perspective for Quantum Computing (QC) is the question whether QC has the potential to reduce the vast resource requirements for training and operating GenAI models. While large-scale generative NLP tasks are currently out of reach for practical quantum computers, the generation of short semantic structures such as passwords is not. Generating passwords that mimic real user behavior has many applications, for example to test an authentication system against realistic threat models. Classical password generation via deep learning have recently been investigated with significant progress in their ability to generate novel, realistic password candidates. In the present work we investigate the utility of adiabatic quantum computers for this task. More precisely, we study different encodings of token strings and propose novel approaches based on the Quadratic Unconstrained Binary Optimization (QUBO) and the Unit-Disk Maximum Independent Set (UD-MIS) problems. Our approach allows us to estimate the token distribution from data and adiabatically prepare a quantum state from which we eventually sample the generated passwords via measurements. Our results show that relatively small samples of 128 passwords, generated on the QuEra Aquila 256-qubit neutral atom quantum computer, contain human-like passwords such as "Tunas200992" or "teedem28iglove".

A Quantum Optimization Case Study for a Transport Robot Scheduling Problem

We present a comprehensive case study comparing the performance of D-Waves' quantum-classical hybrid framework, Fujitsu's quantum-inspired digital annealer, and Gurobi's state-of-the-art classical solver in solving a transport robot scheduling problem. This problem originates from an industrially relevant real-world scenario. We provide three different models for our problem following different design philosophies. In our benchmark, we focus on the solution quality and end-to-end runtime of different model and solver combinations. We find promising results for the digital annealer and some opportunities for the hybrid quantum annealer in direct comparison with Gurobi. Our study provides insights into the workflow for solving an application-oriented optimization problem with different strategies, and can be useful for evaluating the strengths and weaknesses of different approaches.

Explainable Quantum Machine Learning

Methods of artificial intelligence (AI) and especially machine learning (ML) have been growing ever more complex, and at the same time have more and more impact on people's lives. This leads to explainable AI (XAI) manifesting itself as an important research field that helps humans to better comprehend ML systems. In parallel, quantum machine learning (QML) is emerging with the ongoing improvement of quantum computing hardware combined with its increasing availability via cloud services. QML enables quantum-enhanced ML in which quantum mechanics is exploited to facilitate ML tasks, typically in form of quantum-classical hybrid algorithms that combine quantum and classical resources. Quantum gates constitute the building blocks of gate-based quantum hardware and form circuits that can be used for quantum computations. For QML applications, quantum circuits are typically parameterized and their parameters are optimized classically such that a suitably defined objective function is minimized. Inspired by XAI, we raise the question of explainability of such circuits by quantifying the importance of (groups of) gates for specific goals. To this end, we transfer and adapt the well-established concept of Shapley values to the quantum realm. The resulting attributions can be interpreted as explanations for why a specific circuit works well for a given task, improving the understanding of how to construct parameterized (or variational) quantum circuits, and fostering their human interpretability in general. An experimental evaluation on simulators and two superconducting quantum hardware devices demonstrates the benefits of the proposed framework for classification, generative modeling, transpilation, and optimization. Furthermore, our results shed some light on the role of specific gates in popular QML approaches.

Shapley Values with Uncertain Value Functions

We propose a novel definition of Shapley values with uncertain value functions based on first principles using probability theory. Such uncertain value functions can arise in the context of explainable machine learning as a result of non-deterministic algorithms. We show that random effects can in fact be absorbed into a Shapley value with a noiseless but shifted value function. Hence, Shapley values with uncertain value functions can be used in analogy to regular Shapley values. However, their reliable evaluation typically requires more computational effort.

Quantum Feature Selection

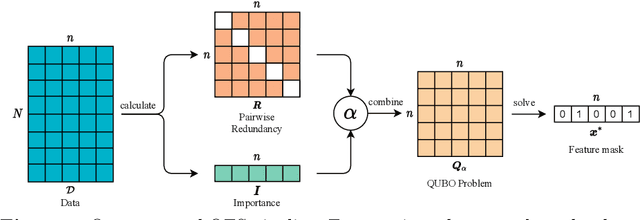
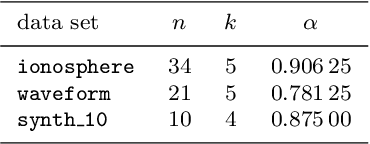
In machine learning, fewer features reduce model complexity. Carefully assessing the influence of each input feature on the model quality is therefore a crucial preprocessing step. We propose a novel feature selection algorithm based on a quadratic unconstrained binary optimization (QUBO) problem, which allows to select a specified number of features based on their importance and redundancy. In contrast to iterative or greedy methods, our direct approach yields higherquality solutions. QUBO problems are particularly interesting because they can be solved on quantum hardware. To evaluate our proposed algorithm, we conduct a series of numerical experiments using a classical computer, a quantum gate computer and a quantum annealer. Our evaluation compares our method to a range of standard methods on various benchmark datasets. We observe competitive performance.

On the effects of biased quantum random numbers on the initialization of artificial neural networks

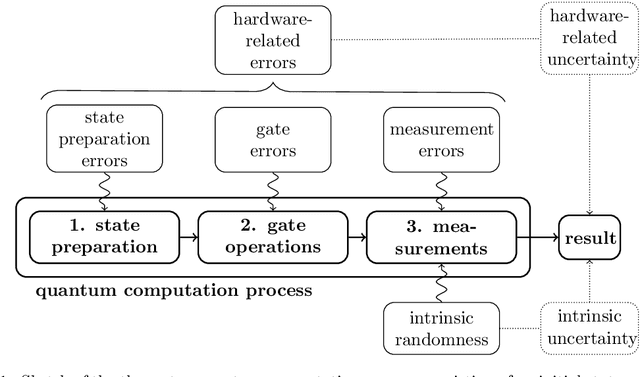
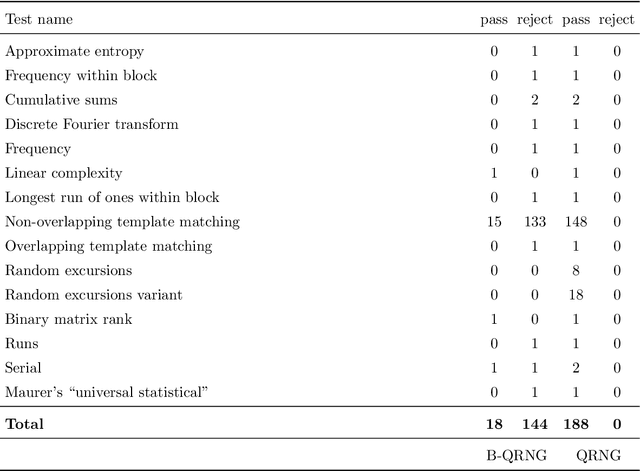
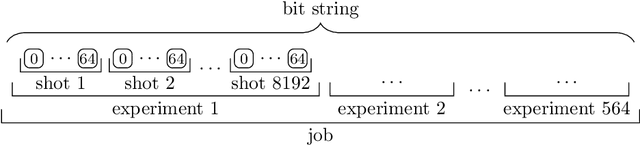
Recent advances in practical quantum computing have led to a variety of cloud-based quantum computing platforms that allow researchers to evaluate their algorithms on noisy intermediate-scale quantum (NISQ) devices. A common property of quantum computers is that they exhibit instances of true randomness as opposed to pseudo-randomness obtained from classical systems. Investigating the effects of such true quantum randomness in the context of machine learning is appealing, and recent results vaguely suggest that benefits can indeed be achieved from the use of quantum random numbers. To shed some more light on this topic, we empirically study the effects of hardware-biased quantum random numbers on the initialization of artificial neural network weights in numerical experiments. We find no statistically significant difference in comparison with unbiased quantum random numbers as well as biased and unbiased random numbers from a classical pseudo-random number generator. The quantum random numbers for our experiments are obtained from real quantum hardware.

Representation of binary classification trees with binary features by quantum circuits

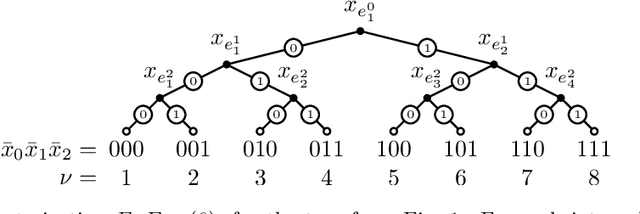
We propose a quantum representation of binary classification trees with binary features based on a probabilistic approach. By using the quantum computer as a processor for probability distributions, a probabilistic traversal of the decision tree can be realized via measurements of a quantum circuit. We describe how tree inductions and the prediction of class labels of query data can be integrated into this framework. An on-demand sampling method enables predictions with a constant number of classical memory slots, independent of the tree depth. We experimentally study our approach using both a quantum computing simulator and actual IBM quantum hardware. To our knowledge, this is the first realization of a decision tree classifier on a quantum device.

Calibrated Simplex Mapping Classification

We propose a novel supervised multi-class/single-label classifier that maps training data onto a linearly separable latent space with a simplex-like geometry. This approach allows us to transform the classification problem into a well-defined regression problem. For its solution we can choose suitable distance metrics in feature space and regression models predicting latent space coordinates. A benchmark on various artificial and real-world data sets is used to demonstrate the calibration qualities and prediction performance of our classifier.

Adaptive Sampling of Pareto Frontiers with Binary Constraints Using Regression and Classification

We present a novel adaptive optimization algorithm for black-box multi-objective optimization problems with binary constraints on the foundation of Bayes optimization. Our method is based on probabilistic regression and classification models, which act as a surrogate for the optimization goals and allow us to suggest multiple design points at once in each iteration. The proposed acquisition function is intuitively understandable and can be tuned to the demands of the problems at hand. We also present a novel ellipsoid truncation method to speed up the expected hypervolume calculation in a straightforward way for regression models with a normal probability density. We benchmark our approach with an evolutionary algorithm on multiple test problems.

CupNet -- Pruning a network for geometric data

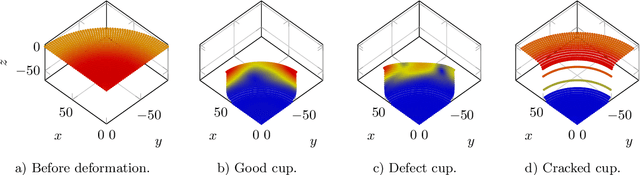
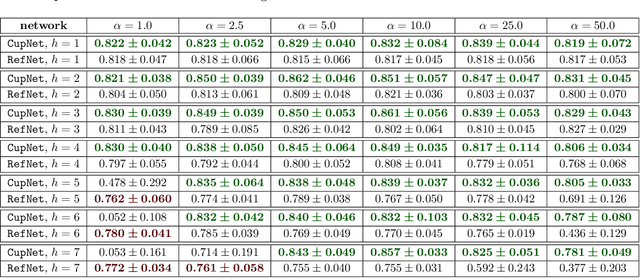
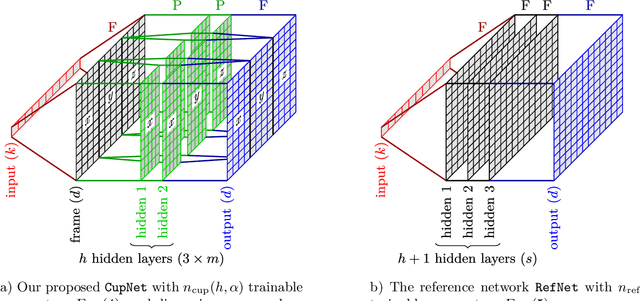
Using data from a simulated cup drawing process, we demonstrate how the inherent geometrical structure of cup meshes can be used to effectively prune an artificial neural network in a straightforward way.