Hybrid Quantum-Classical Multi-Agent Pathfinding

Multi-Agent Path Finding (MAPF) focuses on determining conflict-free paths for multiple agents navigating through a shared space to reach specified goal locations. This problem becomes computationally challenging, particularly when handling large numbers of agents, as frequently encountered in practical applications like coordinating autonomous vehicles. Quantum computing (QC) is a promising candidate in overcoming such limits. However, current quantum hardware is still in its infancy and thus limited in terms of computing power and error robustness. In this work, we present the first optimal hybrid quantum-classical MAPF algorithm which is based on branch-and-cut-and-prize. QC is integrated by iteratively solving QUBO problems, based on conflict graphs. Experiments on actual quantum hardware and results on benchmark data suggest that our approach dominates previous QUBO formulations and baseline MAPF solvers.

Computing Marginal and Conditional Divergences between Decomposable Models with Applications

The ability to compute the exact divergence between two high-dimensional distributions is useful in many applications but doing so naively is intractable. Computing the alpha-beta divergence -- a family of divergences that includes the Kullback-Leibler divergence and Hellinger distance -- between the joint distribution of two decomposable models, i.e chordal Markov networks, can be done in time exponential in the treewidth of these models. However, reducing the dissimilarity between two high-dimensional objects to a single scalar value can be uninformative. Furthermore, in applications such as supervised learning, the divergence over a conditional distribution might be of more interest. Therefore, we propose an approach to compute the exact alpha-beta divergence between any marginal or conditional distribution of two decomposable models. Doing so tractably is non-trivial as we need to decompose the divergence between these distributions and therefore, require a decomposition over the marginal and conditional distributions of these models. Consequently, we provide such a decomposition and also extend existing work to compute the marginal and conditional alpha-beta divergence between these decompositions. We then show how our method can be used to analyze distributional changes by first applying it to a benchmark image dataset. Finally, based on our framework, we propose a novel way to quantify the error in contemporary superconducting quantum computers. Code for all experiments is available at: https://lklee.dev/pub/2023-icdm/code

Estimating Divergences in High Dimensions

The problem of estimating the divergence between 2 high dimensional distributions with limited samples is an important problem in various fields such as machine learning. Although previous methods perform well with moderate dimensional data, their accuracy starts to degrade in situations with 100s of binary variables. Therefore, we propose the use of decomposable models for estimating divergences in high dimensional data. These allow us to factorize the estimated density of the high-dimensional distribution into a product of lower dimensional functions. We conduct formal and experimental analyses to explore the properties of using decomposable models in the context of divergence estimation. To this end, we show empirically that estimating the Kullback-Leibler divergence using decomposable models from a maximum likelihood estimator outperforms existing methods for divergence estimation in situations where dimensionality is high and useful decomposable models can be learnt from the available data.

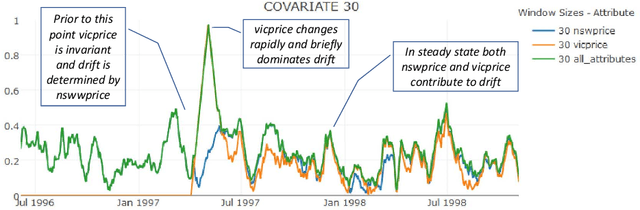
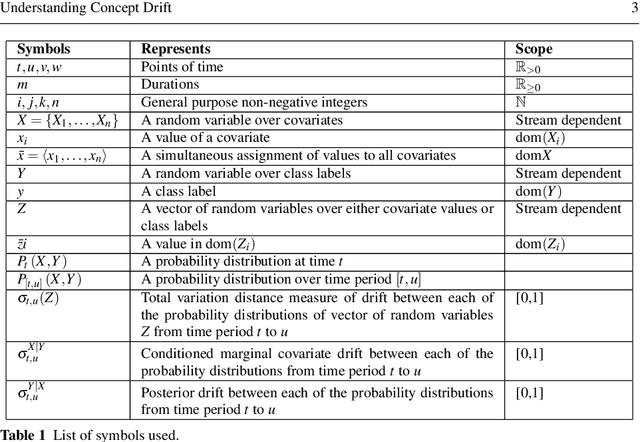
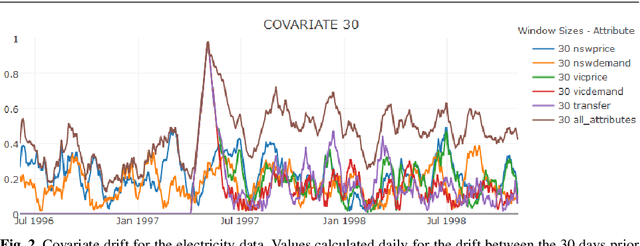
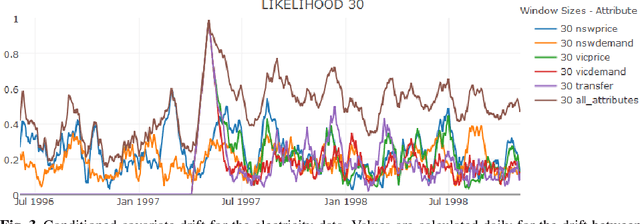
Understanding Concept Drift

Concept drift is a major issue that greatly affects the accuracy and reliability of many real-world applications of machine learning. We argue that to tackle concept drift it is important to develop the capacity to describe and analyze it. We propose tools for this purpose, arguing for the importance of quantitative descriptions of drift in marginal distributions. We present quantitative drift analysis techniques along with methods for communicating their results. We demonstrate their effectiveness by application to three real-world learning tasks.