Dynamic Range Reduction via Branch-and-Bound

The demand for high-performance computing in machine learning and artificial intelligence has led to the development of specialized hardware accelerators like Tensor Processing Units (TPUs), Graphics Processing Units (GPUs), and Field-Programmable Gate Arrays (FPGAs). A key strategy to enhance these accelerators is the reduction of precision in arithmetic operations, which increases processing speed and lowers latency - crucial for real-time AI applications. Precision reduction minimizes memory bandwidth requirements and energy consumption, essential for large-scale and mobile deployments, and increases throughput by enabling more parallel operations per cycle, maximizing hardware resource utilization. This strategy is equally vital for solving NP-hard quadratic unconstrained binary optimization (QUBO) problems common in machine learning, which often require high precision for accurate representation. Special hardware solvers, such as quantum annealers, benefit significantly from precision reduction. This paper introduces a fully principled Branch-and-Bound algorithm for reducing precision needs in QUBO problems by utilizing dynamic range as a measure of complexity. Experiments validate our algorithm's effectiveness on an actual quantum annealer.

Explainable Quantum Machine Learning

Methods of artificial intelligence (AI) and especially machine learning (ML) have been growing ever more complex, and at the same time have more and more impact on people's lives. This leads to explainable AI (XAI) manifesting itself as an important research field that helps humans to better comprehend ML systems. In parallel, quantum machine learning (QML) is emerging with the ongoing improvement of quantum computing hardware combined with its increasing availability via cloud services. QML enables quantum-enhanced ML in which quantum mechanics is exploited to facilitate ML tasks, typically in form of quantum-classical hybrid algorithms that combine quantum and classical resources. Quantum gates constitute the building blocks of gate-based quantum hardware and form circuits that can be used for quantum computations. For QML applications, quantum circuits are typically parameterized and their parameters are optimized classically such that a suitably defined objective function is minimized. Inspired by XAI, we raise the question of explainability of such circuits by quantifying the importance of (groups of) gates for specific goals. To this end, we transfer and adapt the well-established concept of Shapley values to the quantum realm. The resulting attributions can be interpreted as explanations for why a specific circuit works well for a given task, improving the understanding of how to construct parameterized (or variational) quantum circuits, and fostering their human interpretability in general. An experimental evaluation on simulators and two superconducting quantum hardware devices demonstrates the benefits of the proposed framework for classification, generative modeling, transpilation, and optimization. Furthermore, our results shed some light on the role of specific gates in popular QML approaches.

Shapley Values with Uncertain Value Functions

We propose a novel definition of Shapley values with uncertain value functions based on first principles using probability theory. Such uncertain value functions can arise in the context of explainable machine learning as a result of non-deterministic algorithms. We show that random effects can in fact be absorbed into a Shapley value with a noiseless but shifted value function. Hence, Shapley values with uncertain value functions can be used in analogy to regular Shapley values. However, their reliable evaluation typically requires more computational effort.

Towards Bundle Adjustment for Satellite Imaging via Quantum Machine Learning

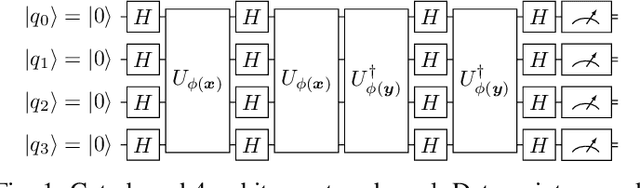
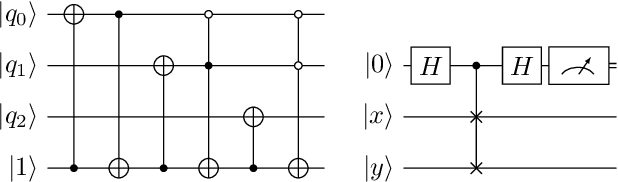
Given is a set of images, where all images show views of the same area at different points in time and from different viewpoints. The task is the alignment of all images such that relevant information, e.g., poses, changes, and terrain, can be extracted from the fused image. In this work, we focus on quantum methods for keypoint extraction and feature matching, due to the demanding computational complexity of these sub-tasks. To this end, k-medoids clustering, kernel density clustering, nearest neighbor search, and kernel methods are investigated and it is explained how these methods can be re-formulated for quantum annealers and gate-based quantum computers. Experimental results obtained on digital quantum emulation hardware, quantum annealers, and quantum gate computers show that classical systems still deliver superior results. However, the proposed methods are ready for the current and upcoming generations of quantum computing devices which have the potential to outperform classical systems in the near future.

QUBOs for Sorting Lists and Building Trees

We show that the fundamental tasks of sorting lists and building search trees or heaps can be modeled as quadratic unconstrained binary optimization problems (QUBOs). The idea is to understand these tasks as permutation problems and to devise QUBOs whose solutions represent appropriate permutation matrices. We discuss how to construct such QUBOs and how to solve them using Hopfield nets or adiabatic) quantum computing. In short, we show that neurocomputing methods or quantum computers can solve problems usually associated with abstract data structures.