Sliding Window Neural Generated Tracking Based on Measurement Model

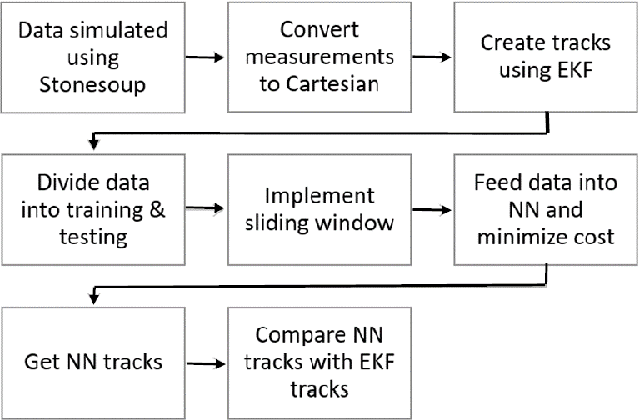
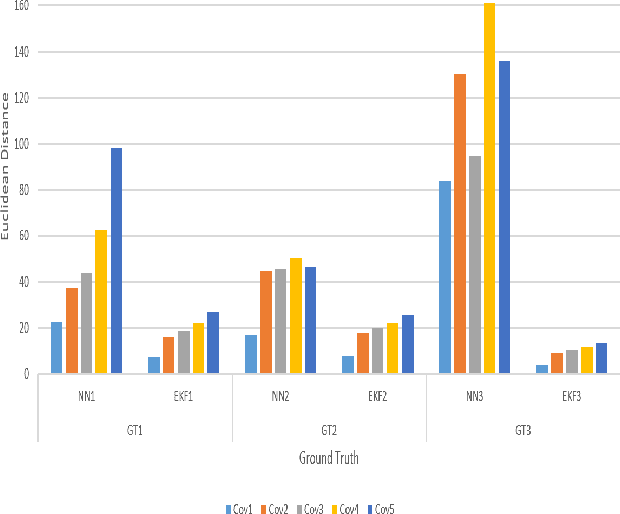
In the pursuit of further advancement in the field of target tracking, this paper explores the efficacy of a feedforward neural network in predicting drones tracks, aiming to eventually, compare the tracks created by the well-known Kalman filter and the ones created by our proposed neural network. The unique feature of our proposed neural network tracker is that it is using only a measurement model to estimate the next states of the track. Object model selection and linearization is one of the challenges that always face in the tracking process. The neural network uses a sliding window to incorporate the history of measurements when applying estimations of the track values. The testing results are comparable to the ones generated by the Kalman filter, especially for the cases where there is low measurement covariance. The complexity of linearization is avoided when using this proposed model.

Towards Bundle Adjustment for Satellite Imaging via Quantum Machine Learning

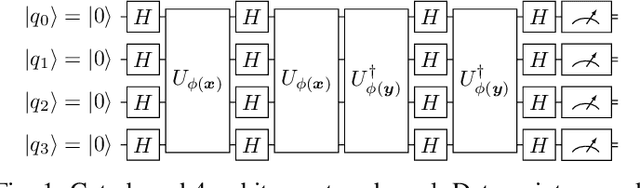
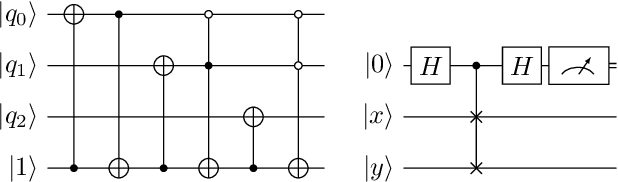
Given is a set of images, where all images show views of the same area at different points in time and from different viewpoints. The task is the alignment of all images such that relevant information, e.g., poses, changes, and terrain, can be extracted from the fused image. In this work, we focus on quantum methods for keypoint extraction and feature matching, due to the demanding computational complexity of these sub-tasks. To this end, k-medoids clustering, kernel density clustering, nearest neighbor search, and kernel methods are investigated and it is explained how these methods can be re-formulated for quantum annealers and gate-based quantum computers. Experimental results obtained on digital quantum emulation hardware, quantum annealers, and quantum gate computers show that classical systems still deliver superior results. However, the proposed methods are ready for the current and upcoming generations of quantum computing devices which have the potential to outperform classical systems in the near future.

Riemannian batch normalization for SPD neural networks

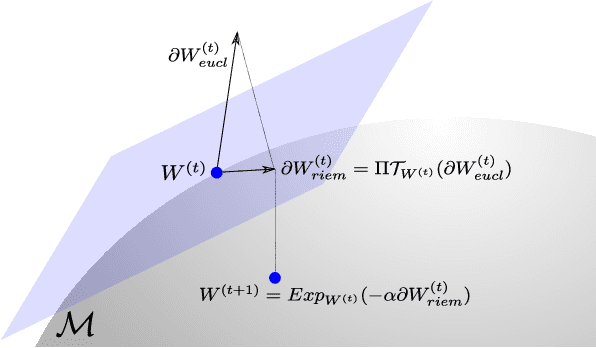
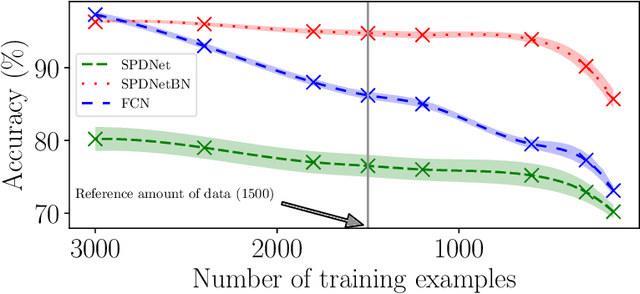
Covariance matrices have attracted attention for machine learning applications due to their capacity to capture interesting structure in the data. The main challenge is that one needs to take into account the particular geometry of the Riemannian manifold of symmetric positive definite (SPD) matrices they belong to. In the context of deep networks, several architectures for these matrices have recently been proposed. In our article, we introduce a Riemannian batch normalization (batchnorm) algorithm, which generalizes the one used in Euclidean nets. This novel layer makes use of geometric operations on the manifold, notably the Riemannian barycenter, parallel transport and non-linear structured matrix transformations. We derive a new manifold-constrained gradient descent algorithm working in the space of SPD matrices, allowing to learn the batchnorm layer. We validate our proposed approach with experiments in three different contexts on diverse data types: a drone recognition dataset from radar observations, and on emotion and action recognition datasets from video and motion capture data. Experiments show that the Riemannian batchnorm systematically gives better classification performance compared with leading methods and a remarkable robustness to lack of data.