Efficient Parameter Estimation for Bayesian Network Classifiers using Hierarchical Linear Smoothing

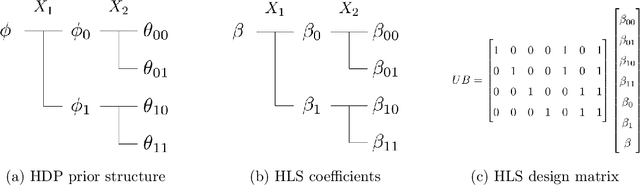
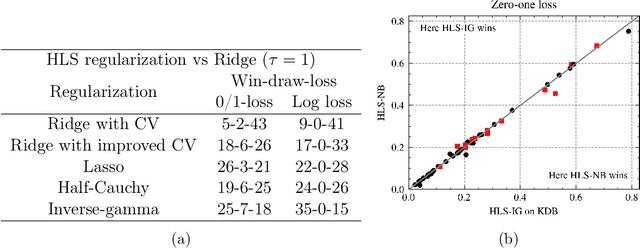
Bayesian network classifiers (BNCs) possess a number of properties desirable for a modern classifier: They are easily interpretable, highly scalable, and offer adaptable complexity. However, traditional methods for learning BNCs have historically underperformed when compared to leading classification methods such as random forests. Recent parameter smoothing techniques using hierarchical Dirichlet processes (HDPs) have enabled BNCs to achieve performance competitive with random forests on categorical data, but these techniques are relatively inflexible, and require a complicated, specialized sampling process. In this paper, we introduce a novel method for parameter estimation that uses a log-linear regression to approximate the behaviour of HDPs. As a linear model, our method is remarkably flexible and simple to interpret, and can leverage the vast literature on learning linear models. Our experiments show that our method can outperform HDP smoothing while being orders of magnitude faster, remaining competitive with random forests on categorical data.

Improving Random Forests by Smoothing

Gaussian process regression is a popular model in the small data regime due to its sound uncertainty quantification and the exploitation of the smoothness of the regression function that is encountered in a wide range of practical problems. However, Gaussian processes perform sub-optimally when the degree of smoothness is non-homogeneous across the input domain. Random forest regression partially addresses this issue by providing local basis functions of variable support set sizes that are chosen in a data-driven way. However, they do so at the expense of forgoing any degree of smoothness, which often results in poor performance in the small data regime. Here, we aim to combine the advantages of both models by applying a kernel-based smoothing mechanism to a learned random forest or any other piecewise constant prediction function. As we demonstrate empirically, the resulting model consistently improves the predictive performance of the underlying random forests and, in almost all test cases, also improves the log loss of the usual uncertainty quantification based on inter-tree variance. The latter advantage can be attributed to the ability of the smoothing model to take into account the uncertainty over the exact tree-splitting locations.

MONSTER: Monash Scalable Time Series Evaluation Repository

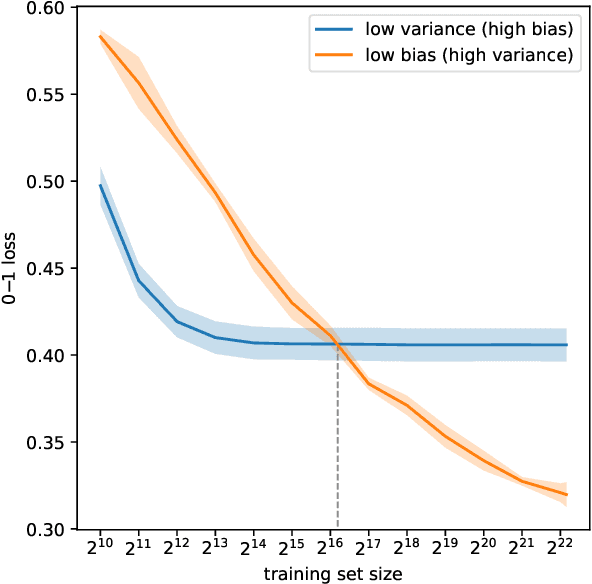
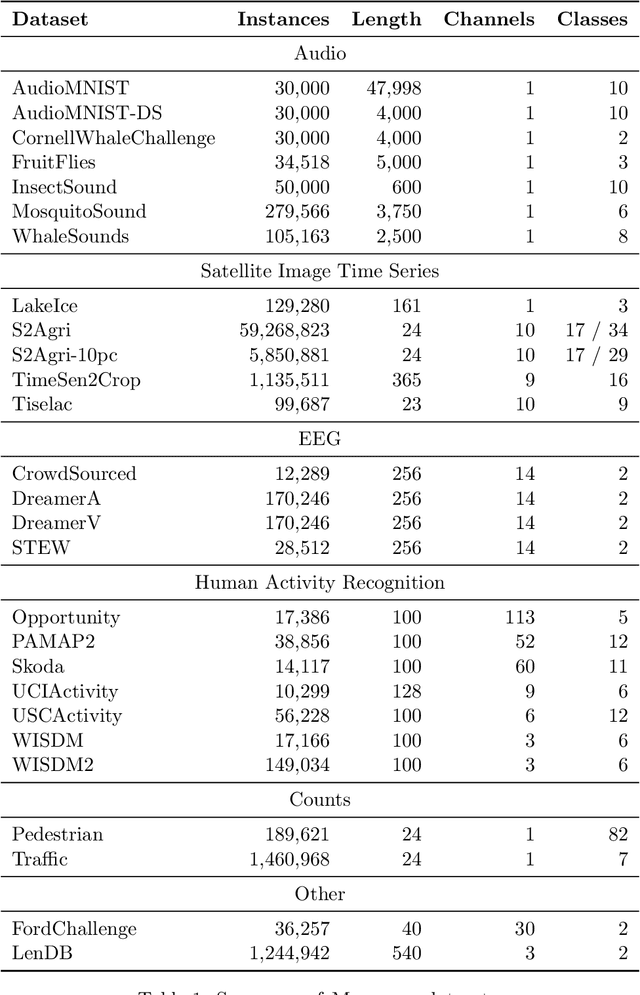
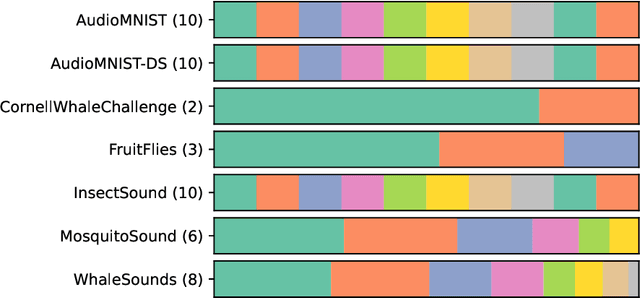
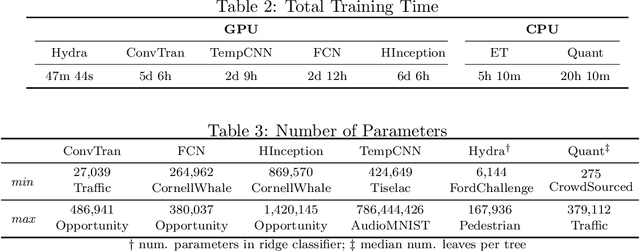
We introduce MONSTER-the MONash Scalable Time Series Evaluation Repository-a collection of large datasets for time series classification. The field of time series classification has benefitted from common benchmarks set by the UCR and UEA time series classification repositories. However, the datasets in these benchmarks are small, with median sizes of 217 and 255 examples, respectively. In consequence they favour a narrow subspace of models that are optimised to achieve low classification error on a wide variety of smaller datasets, that is, models that minimise variance, and give little weight to computational issues such as scalability. Our hope is to diversify the field by introducing benchmarks using larger datasets. We believe that there is enormous potential for new progress in the field by engaging with the theoretical and practical challenges of learning effectively from larger quantities of data.

Fast Gibbs sampling for the local and global trend Bayesian exponential smoothing model

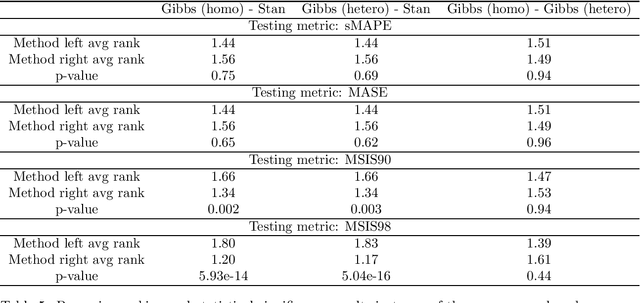
In Smyl et al. [Local and global trend Bayesian exponential smoothing models. International Journal of Forecasting, 2024.], a generalised exponential smoothing model was proposed that is able to capture strong trends and volatility in time series. This method achieved state-of-the-art performance in many forecasting tasks, but its fitting procedure, which is based on the NUTS sampler, is very computationally expensive. In this work, we propose several modifications to the original model, as well as a bespoke Gibbs sampler for posterior exploration; these changes improve sampling time by an order of magnitude, thus rendering the model much more practically relevant. The new model, and sampler, are evaluated on the M3 dataset and are shown to be competitive, or superior, in terms of accuracy to the original method, while being substantially faster to run.

Prevalidated ridge regression is a highly-efficient drop-in replacement for logistic regression for high-dimensional data

Logistic regression is a ubiquitous method for probabilistic classification. However, the effectiveness of logistic regression depends upon careful and relatively computationally expensive tuning, especially for the regularisation hyperparameter, and especially in the context of high-dimensional data. We present a prevalidated ridge regression model that closely matches logistic regression in terms of classification error and log-loss, particularly for high-dimensional data, while being significantly more computationally efficient and having effectively no hyperparameters beyond regularisation. We scale the coefficients of the model so as to minimise log-loss for a set of prevalidated predictions derived from the estimated leave-one-out cross-validation error. This exploits quantities already computed in the course of fitting the ridge regression model in order to find the scaling parameter with nominal additional computational expense.

Bayes beats Cross Validation: Efficient and Accurate Ridge Regression via Expectation Maximization

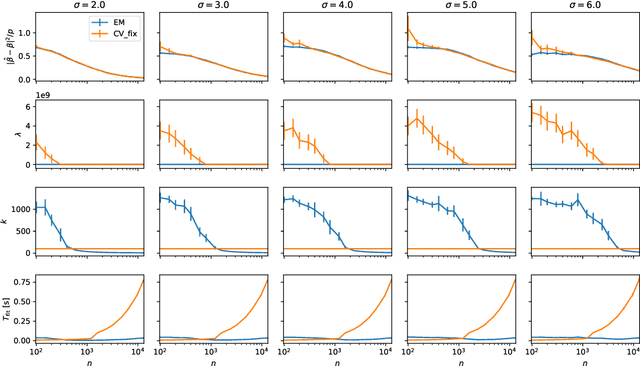
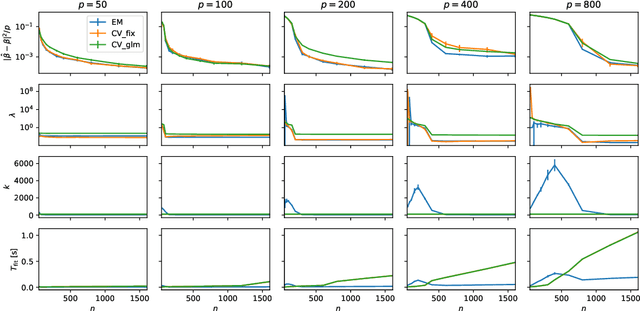
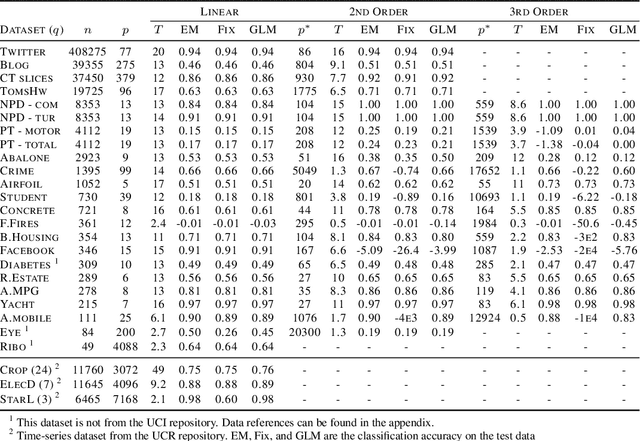
We present a novel method for tuning the regularization hyper-parameter, $\lambda$, of a ridge regression that is faster to compute than leave-one-out cross-validation (LOOCV) while yielding estimates of the regression parameters of equal, or particularly in the setting of sparse covariates, superior quality to those obtained by minimising the LOOCV risk. The LOOCV risk can suffer from multiple and bad local minima for finite $n$ and thus requires the specification of a set of candidate $\lambda$, which can fail to provide good solutions. In contrast, we show that the proposed method is guaranteed to find a unique optimal solution for large enough $n$, under relatively mild conditions, without requiring the specification of any difficult to determine hyper-parameters. This is based on a Bayesian formulation of ridge regression that we prove to have a unimodal posterior for large enough $n$, allowing for both the optimal $\lambda$ and the regression coefficients to be jointly learned within an iterative expectation maximization (EM) procedure. Importantly, we show that by utilizing an appropriate preprocessing step, a single iteration of the main EM loop can be implemented in $O(\min(n, p))$ operations, for input data with $n$ rows and $p$ columns. In contrast, evaluating a single value of $\lambda$ using fast LOOCV costs $O(n \min(n, p))$ operations when using the same preprocessing. This advantage amounts to an asymptotic improvement of a factor of $l$ for $l$ candidate values for $\lambda$ (in the regime $q, p \in O(\sqrt{n})$ where $q$ is the number of regression targets).

Scalable Probabilistic Forecasting in Retail with Gradient Boosted Trees: A Practitioner's Approach

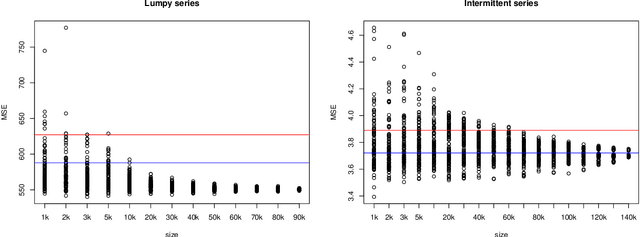
The recent M5 competition has advanced the state-of-the-art in retail forecasting. However, we notice important differences between the competition challenge and the challenges we face in a large e-commerce company. The datasets in our scenario are larger (hundreds of thousands of time series), and e-commerce can afford to have a larger assortment than brick-and-mortar retailers, leading to more intermittent data. To scale to larger dataset sizes with feasible computational effort, firstly, we investigate a two-layer hierarchy and propose a top-down approach to forecasting at an aggregated level with less amount of series and intermittency, and then disaggregating to obtain the decision-level forecasts. Probabilistic forecasts are generated under distributional assumptions. Secondly, direct training at the lower level with subsamples can also be an alternative way of scaling. Performance of modelling with subsets is evaluated with the main dataset. Apart from a proprietary dataset, the proposed scalable methods are evaluated using the Favorita dataset and the M5 dataset. We are able to show the differences in characteristics of the e-commerce and brick-and-mortar retail datasets. Notably, our top-down forecasting framework enters the top 50 of the original M5 competition, even with models trained at a higher level under a much simpler setting.

Computing Marginal and Conditional Divergences between Decomposable Models with Applications

The ability to compute the exact divergence between two high-dimensional distributions is useful in many applications but doing so naively is intractable. Computing the alpha-beta divergence -- a family of divergences that includes the Kullback-Leibler divergence and Hellinger distance -- between the joint distribution of two decomposable models, i.e chordal Markov networks, can be done in time exponential in the treewidth of these models. However, reducing the dissimilarity between two high-dimensional objects to a single scalar value can be uninformative. Furthermore, in applications such as supervised learning, the divergence over a conditional distribution might be of more interest. Therefore, we propose an approach to compute the exact alpha-beta divergence between any marginal or conditional distribution of two decomposable models. Doing so tractably is non-trivial as we need to decompose the divergence between these distributions and therefore, require a decomposition over the marginal and conditional distributions of these models. Consequently, we provide such a decomposition and also extend existing work to compute the marginal and conditional alpha-beta divergence between these decompositions. We then show how our method can be used to analyze distributional changes by first applying it to a benchmark image dataset. Finally, based on our framework, we propose a novel way to quantify the error in contemporary superconducting quantum computers. Code for all experiments is available at: https://lklee.dev/pub/2023-icdm/code

QUANT: A Minimalist Interval Method for Time Series Classification

We show that it is possible to achieve the same accuracy, on average, as the most accurate existing interval methods for time series classification on a standard set of benchmark datasets using a single type of feature (quantiles), fixed intervals, and an 'off the shelf' classifier. This distillation of interval-based approaches represents a fast and accurate method for time series classification, achieving state-of-the-art accuracy on the expanded set of 142 datasets in the UCR archive with a total compute time (training and inference) of less than 15 minutes using a single CPU core.

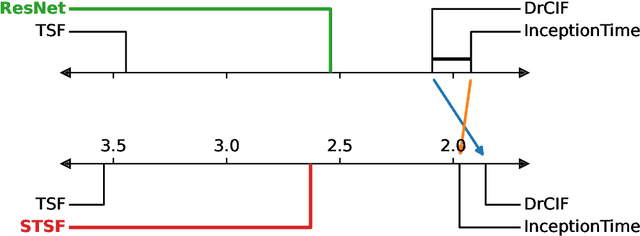
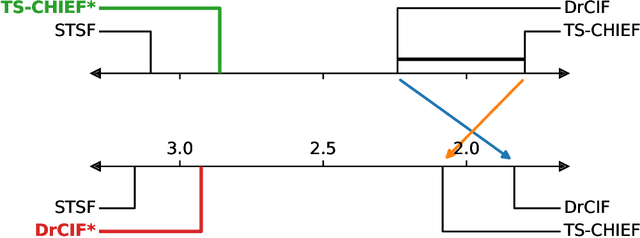
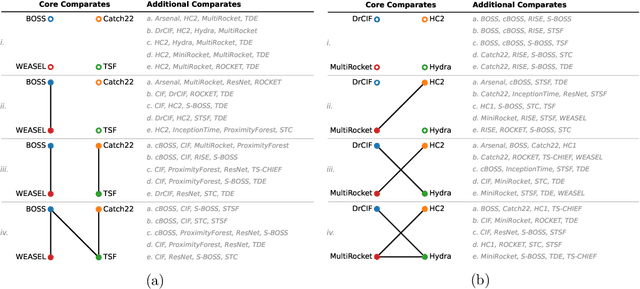
An Approach to Multiple Comparison Benchmark Evaluations that is Stable Under Manipulation of the Comparate Set

The measurement of progress using benchmarks evaluations is ubiquitous in computer science and machine learning. However, common approaches to analyzing and presenting the results of benchmark comparisons of multiple algorithms over multiple datasets, such as the critical difference diagram introduced by Dem\v{s}ar (2006), have important shortcomings and, we show, are open to both inadvertent and intentional manipulation. To address these issues, we propose a new approach to presenting the results of benchmark comparisons, the Multiple Comparison Matrix (MCM), that prioritizes pairwise comparisons and precludes the means of manipulating experimental results in existing approaches. MCM can be used to show the results of an all-pairs comparison, or to show the results of a comparison between one or more selected algorithms and the state of the art. MCM is implemented in Python and is publicly available.