Mario Boley
Interpretable Representation Learning for Additive Rule Ensembles
Jun 26, 2025



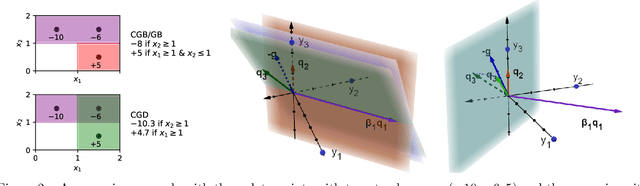
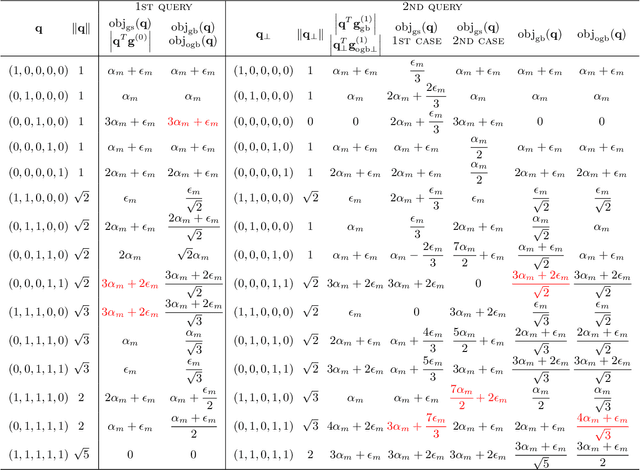
Abstract:Small additive ensembles of symbolic rules offer interpretable prediction models. Traditionally, these ensembles use rule conditions based on conjunctions of simple threshold propositions $x \geq t$ on a single input variable $x$ and threshold $t$, resulting geometrically in axis-parallel polytopes as decision regions. While this form ensures a high degree of interpretability for individual rules and can be learned efficiently using the gradient boosting approach, it relies on having access to a curated set of expressive and ideally independent input features so that a small ensemble of axis-parallel regions can describe the target variable well. Absent such features, reaching sufficient accuracy requires increasing the number and complexity of individual rules, which diminishes the interpretability of the model. Here, we extend classical rule ensembles by introducing logical propositions with learnable sparse linear transformations of input variables, i.e., propositions of the form $\mathbf{x}^\mathrm{T}\mathbf{w} \geq t$, where $\mathbf{w}$ is a learnable sparse weight vector, enabling decision regions as general polytopes with oblique faces. We propose a learning method using sequential greedy optimization based on an iteratively reweighted formulation of logistic regression. Experimental results demonstrate that the proposed method efficiently constructs rule ensembles with the same test risk as state-of-the-art methods while significantly reducing model complexity across ten benchmark datasets.
Improving Random Forests by Smoothing
May 11, 2025Abstract:Gaussian process regression is a popular model in the small data regime due to its sound uncertainty quantification and the exploitation of the smoothness of the regression function that is encountered in a wide range of practical problems. However, Gaussian processes perform sub-optimally when the degree of smoothness is non-homogeneous across the input domain. Random forest regression partially addresses this issue by providing local basis functions of variable support set sizes that are chosen in a data-driven way. However, they do so at the expense of forgoing any degree of smoothness, which often results in poor performance in the small data regime. Here, we aim to combine the advantages of both models by applying a kernel-based smoothing mechanism to a learned random forest or any other piecewise constant prediction function. As we demonstrate empirically, the resulting model consistently improves the predictive performance of the underlying random forests and, in almost all test cases, also improves the log loss of the usual uncertainty quantification based on inter-tree variance. The latter advantage can be attributed to the ability of the smoothing model to take into account the uncertainty over the exact tree-splitting locations.
Orthogonal Gradient Boosting for Simpler Additive Rule Ensembles
Feb 24, 2024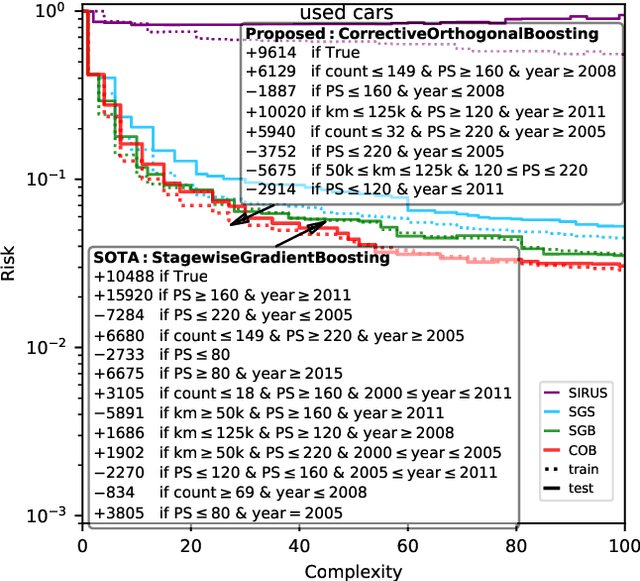
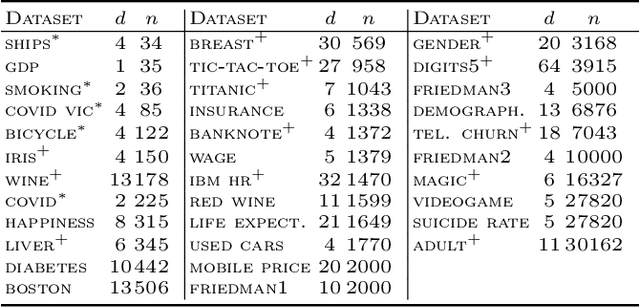
Abstract:Gradient boosting of prediction rules is an efficient approach to learn potentially interpretable yet accurate probabilistic models. However, actual interpretability requires to limit the number and size of the generated rules, and existing boosting variants are not designed for this purpose. Though corrective boosting refits all rule weights in each iteration to minimise prediction risk, the included rule conditions tend to be sub-optimal, because commonly used objective functions fail to anticipate this refitting. Here, we address this issue by a new objective function that measures the angle between the risk gradient vector and the projection of the condition output vector onto the orthogonal complement of the already selected conditions. This approach correctly approximate the ideal update of adding the risk gradient itself to the model and favours the inclusion of more general and thus shorter rules. As we demonstrate using a wide range of prediction tasks, this significantly improves the comprehensibility/accuracy trade-off of the fitted ensemble. Additionally, we show how objective values for related rule conditions can be computed incrementally to avoid any substantial computational overhead of the new method.
From Prediction to Action: Critical Role of Performance Estimation for Machine-Learning-Driven Materials Discovery
Dec 07, 2023Abstract:Materials discovery driven by statistical property models is an iterative decision process, during which an initial data collection is extended with new data proposed by a model-informed acquisition function--with the goal to maximize a certain "reward" over time, such as the maximum property value discovered so far. While the materials science community achieved much progress in developing property models that predict well on average with respect to the training distribution, this form of in-distribution performance measurement is not directly coupled with the discovery reward. This is because an iterative discovery process has a shifting reward distribution that is over-proportionally determined by the model performance for exceptional materials. We demonstrate this problem using the example of bulk modulus maximization among double perovskite oxides. We find that the in-distribution predictive performance suggests random forests as superior to Gaussian process regression, while the results are inverse in terms of the discovery rewards. We argue that the lack of proper performance estimation methods from pre-computed data collections is a fundamental problem for improving data-driven materials discovery, and we propose a novel such estimator that, in contrast to na\"ive reward estimation, successfully predicts Gaussian processes with the "expected improvement" acquisition function as the best out of four options in our demonstrational study for double perovskites. Importantly, it does so without requiring the over thousand ab initio computations that were needed to confirm this prediction.
Bayes beats Cross Validation: Efficient and Accurate Ridge Regression via Expectation Maximization
Nov 03, 2023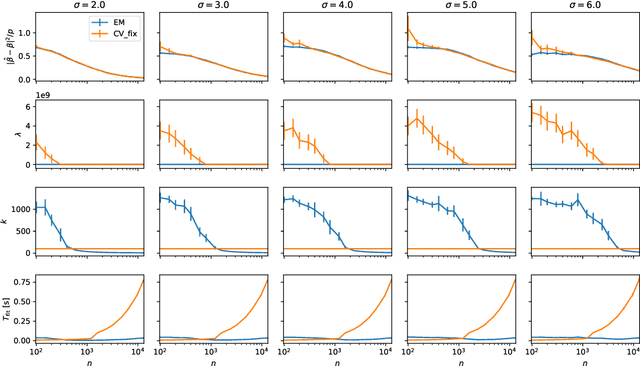

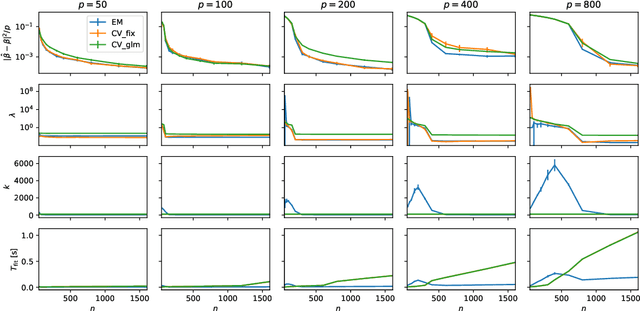
Abstract:We present a novel method for tuning the regularization hyper-parameter, $\lambda$, of a ridge regression that is faster to compute than leave-one-out cross-validation (LOOCV) while yielding estimates of the regression parameters of equal, or particularly in the setting of sparse covariates, superior quality to those obtained by minimising the LOOCV risk. The LOOCV risk can suffer from multiple and bad local minima for finite $n$ and thus requires the specification of a set of candidate $\lambda$, which can fail to provide good solutions. In contrast, we show that the proposed method is guaranteed to find a unique optimal solution for large enough $n$, under relatively mild conditions, without requiring the specification of any difficult to determine hyper-parameters. This is based on a Bayesian formulation of ridge regression that we prove to have a unimodal posterior for large enough $n$, allowing for both the optimal $\lambda$ and the regression coefficients to be jointly learned within an iterative expectation maximization (EM) procedure. Importantly, we show that by utilizing an appropriate preprocessing step, a single iteration of the main EM loop can be implemented in $O(\min(n, p))$ operations, for input data with $n$ rows and $p$ columns. In contrast, evaluating a single value of $\lambda$ using fast LOOCV costs $O(n \min(n, p))$ operations when using the same preprocessing. This advantage amounts to an asymptotic improvement of a factor of $l$ for $l$ candidate values for $\lambda$ (in the regime $q, p \in O(\sqrt{n})$ where $q$ is the number of regression targets).
Better Short than Greedy: Interpretable Models through Optimal Rule Boosting
Jan 21, 2021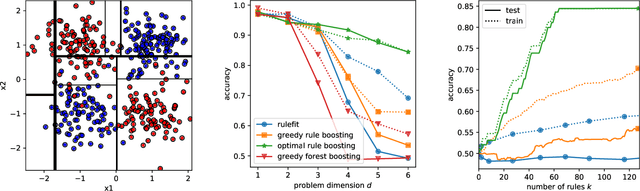
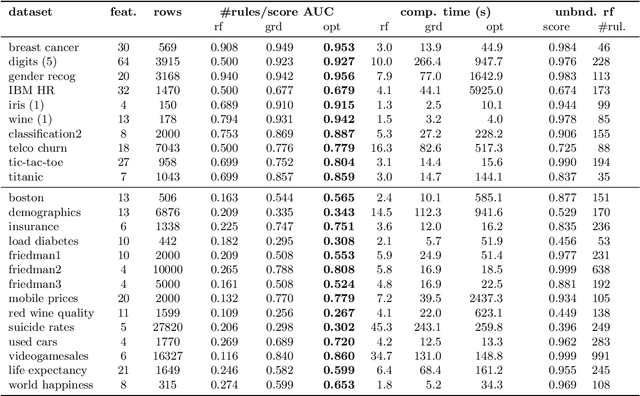
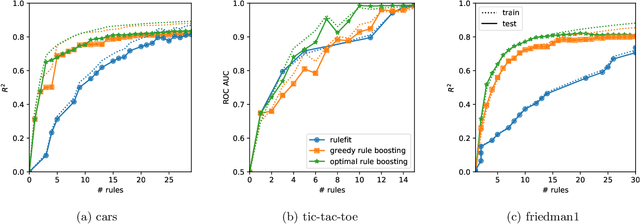
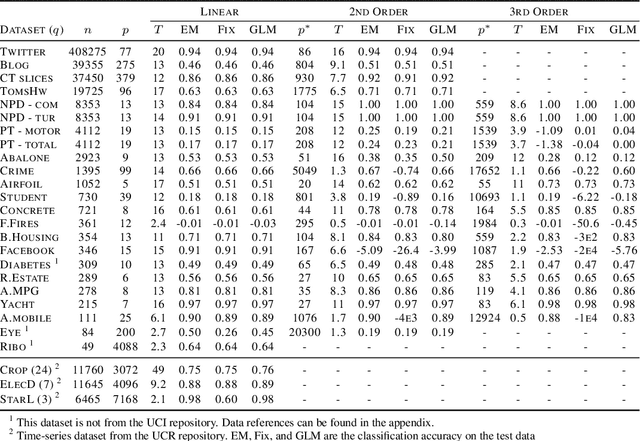
Abstract:Rule ensembles are designed to provide a useful trade-off between predictive accuracy and model interpretability. However, the myopic and random search components of current rule ensemble methods can compromise this goal: they often need more rules than necessary to reach a certain accuracy level or can even outright fail to accurately model a distribution that can actually be described well with a few rules. Here, we present a novel approach aiming to fit rule ensembles of maximal predictive power for a given ensemble size (and thus model comprehensibility). In particular, we present an efficient branch-and-bound algorithm that optimally solves the per-rule objective function of the popular second-order gradient boosting framework. Our main insight is that the boosting objective can be tightly bounded in linear time of the number of covered data points. Along with an additional novel pruning technique related to rule redundancy, this leads to a computationally feasible approach for boosting optimal rules that, as we demonstrate on a wide range of common benchmark problems, consistently outperforms the predictive performance of boosting greedy rules.
Discovering Reliable Causal Rules
Sep 08, 2020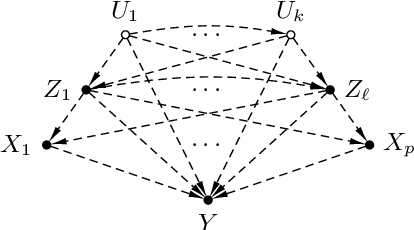
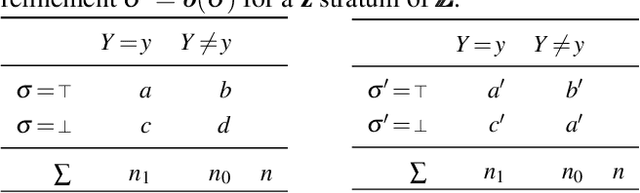
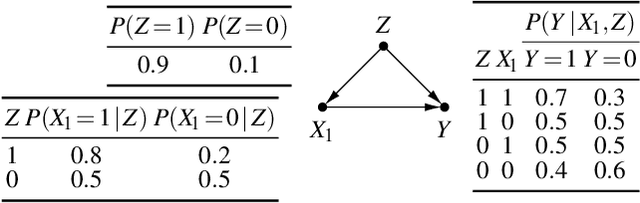
Abstract:We study the problem of deriving policies, or rules, that when enacted on a complex system, cause a desired outcome. Absent the ability to perform controlled experiments, such rules have to be inferred from past observations of the system's behaviour. This is a challenging problem for two reasons: First, observational effects are often unrepresentative of the underlying causal effect because they are skewed by the presence of confounding factors. Second, naive empirical estimations of a rule's effect have a high variance, and, hence, their maximisation can lead to random results. To address these issues, first we measure the causal effect of a rule from observational data---adjusting for the effect of potential confounders. Importantly, we provide a graphical criteria under which causal rule discovery is possible. Moreover, to discover reliable causal rules from a sample, we propose a conservative and consistent estimator of the causal effect, and derive an efficient and exact algorithm that maximises the estimator. On synthetic data, the proposed estimator converges faster to the ground truth than the naive estimator and recovers relevant causal rules even at small sample sizes. Extensive experiments on a variety of real-world datasets show that the proposed algorithm is efficient and discovers meaningful rules.
Communication-Efficient Distributed Online Learning with Kernels
Nov 28, 2019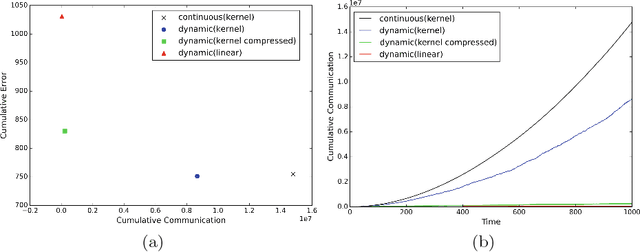
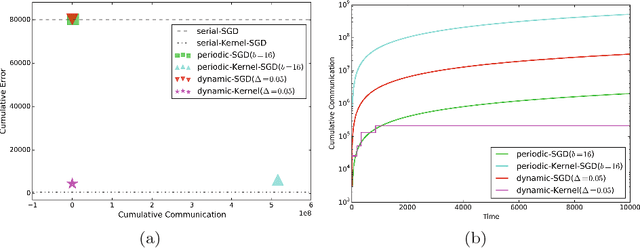
Abstract:We propose an efficient distributed online learning protocol for low-latency real-time services. It extends a previously presented protocol to kernelized online learners that represent their models by a support vector expansion. While such learners often achieve higher predictive performance than their linear counterparts, communicating the support vector expansions becomes inefficient for large numbers of support vectors. The proposed extension allows for a larger class of online learning algorithms---including those alleviating the problem above through model compression. In addition, we characterize the quality of the proposed protocol by introducing a novel criterion that requires the communication to be bounded by the loss suffered.
Adaptive Communication Bounds for Distributed Online Learning
Nov 28, 2019Abstract:We consider distributed online learning protocols that control the exchange of information between local learners in a round-based learning scenario. The learning performance of such a protocol is intuitively optimal if approximately the same loss is incurred as in a hypothetical serial setting. If a protocol accomplishes this, it is inherently impossible to achieve a strong communication bound at the same time. In the worst case, every input is essential for the learning performance, even for the serial setting, and thus needs to be exchanged between the local learners. However, it is reasonable to demand a bound that scales well with the hardness of the serialized prediction problem, as measured by the loss received by a serial online learning algorithm. We provide formal criteria based on this intuition and show that they hold for a simplified version of a previously published protocol.
Discovering Reliable Correlations in Categorical Data
Aug 30, 2019
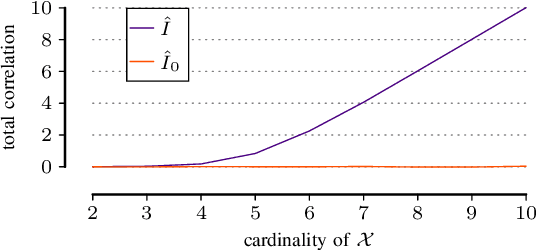
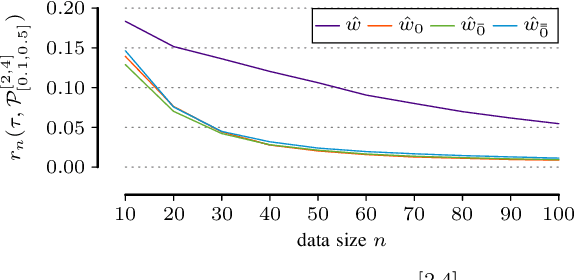

Abstract:In many scientific tasks we are interested in discovering whether there exist any correlations in our data. This raises many questions, such as how to reliably and interpretably measure correlation between a multivariate set of attributes, how to do so without having to make assumptions on distribution of the data or the type of correlation, and, how to efficiently discover the top-most reliably correlated attribute sets from data. In this paper we answer these questions for discovery tasks in categorical data. In particular, we propose a corrected-for-chance, consistent, and efficient estimator for normalized total correlation, by which we obtain a reliable, naturally interpretable, non-parametric measure for correlation over multivariate sets. For the discovery of the top-k correlated sets, we derive an effective algorithmic framework based on a tight bounding function. This framework offers exact, approximate, and heuristic search. Empirical evaluation shows that already for small sample sizes the estimator leads to low-regret optimization outcomes, while the algorithms are shown to be highly effective for both large and high-dimensional data. Through two case studies we confirm that our discovery framework identifies interesting and meaningful correlations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge