Discovering Reliable Correlations in Categorical Data

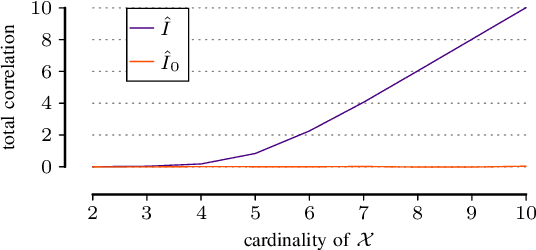
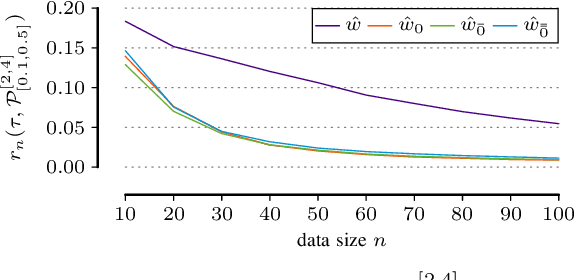
In many scientific tasks we are interested in discovering whether there exist any correlations in our data. This raises many questions, such as how to reliably and interpretably measure correlation between a multivariate set of attributes, how to do so without having to make assumptions on distribution of the data or the type of correlation, and, how to efficiently discover the top-most reliably correlated attribute sets from data. In this paper we answer these questions for discovery tasks in categorical data. In particular, we propose a corrected-for-chance, consistent, and efficient estimator for normalized total correlation, by which we obtain a reliable, naturally interpretable, non-parametric measure for correlation over multivariate sets. For the discovery of the top-k correlated sets, we derive an effective algorithmic framework based on a tight bounding function. This framework offers exact, approximate, and heuristic search. Empirical evaluation shows that already for small sample sizes the estimator leads to low-regret optimization outcomes, while the algorithms are shown to be highly effective for both large and high-dimensional data. Through two case studies we confirm that our discovery framework identifies interesting and meaningful correlations.

Discovering Reliable Dependencies from Data: Hardness and Improved Algorithms

The reliable fraction of information is an attractive score for quantifying (functional) dependencies in high-dimensional data. In this paper, we systematically explore the algorithmic implications of using this measure for optimization. We show that the problem is NP-hard, which justifies the usage of worst-case exponential-time as well as heuristic search methods. We then substantially improve the practical performance for both optimization styles by deriving a novel admissible bounding function that has an unbounded potential for additional pruning over the previously proposed one. Finally, we empirically investigate the approximation ratio of the greedy algorithm and show that it produces highly competitive results in a fraction of time needed for complete branch-and-bound style search.

Discovering Reliable Approximate Functional Dependencies

Given a database and a target attribute of interest, how can we tell whether there exists a functional, or approximately functional dependence of the target on any set of other attributes in the data? How can we reliably, without bias to sample size or dimensionality, measure the strength of such a dependence? And, how can we efficiently discover the optimal or $\alpha$-approximate top-$k$ dependencies? These are exactly the questions we answer in this paper. As we want to be agnostic on the form of the dependence, we adopt an information-theoretic approach, and construct a reliable, bias correcting score that can be efficiently computed. Moreover, we give an effective optimistic estimator of this score, by which for the first time we can mine the approximate functional dependencies from data with guarantees of optimality. Empirical evaluation shows that the derived score achieves a good bias for variance trade-off, can be used within an efficient discovery algorithm, and indeed discovers meaningful dependencies. Most important, it remains reliable in the face of data sparsity.