Better Short than Greedy: Interpretable Models through Optimal Rule Boosting
Paper and Code
Jan 21, 2021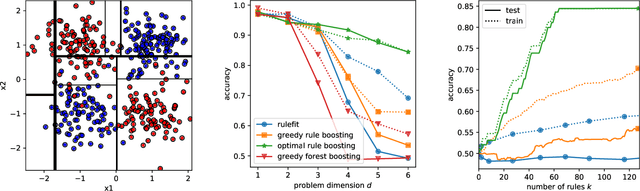
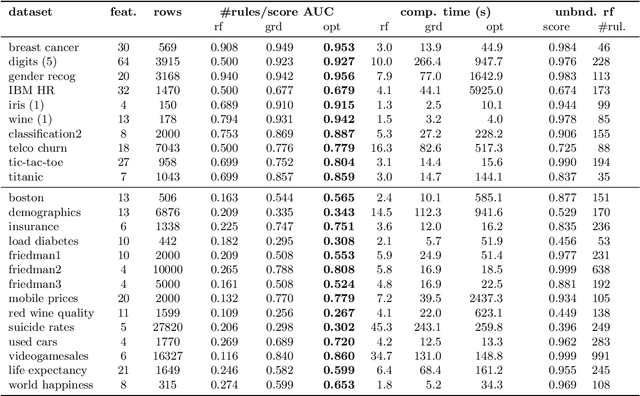
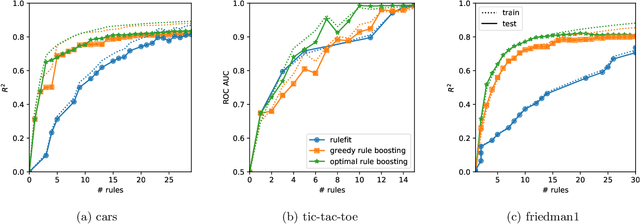
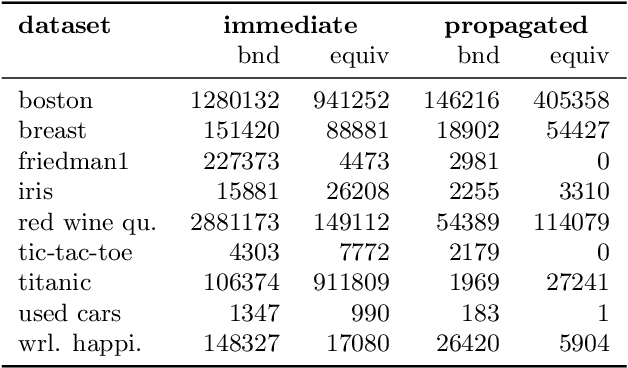
Rule ensembles are designed to provide a useful trade-off between predictive accuracy and model interpretability. However, the myopic and random search components of current rule ensemble methods can compromise this goal: they often need more rules than necessary to reach a certain accuracy level or can even outright fail to accurately model a distribution that can actually be described well with a few rules. Here, we present a novel approach aiming to fit rule ensembles of maximal predictive power for a given ensemble size (and thus model comprehensibility). In particular, we present an efficient branch-and-bound algorithm that optimally solves the per-rule objective function of the popular second-order gradient boosting framework. Our main insight is that the boosting objective can be tightly bounded in linear time of the number of covered data points. Along with an additional novel pruning technique related to rule redundancy, this leads to a computationally feasible approach for boosting optimal rules that, as we demonstrate on a wide range of common benchmark problems, consistently outperforms the predictive performance of boosting greedy rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge