Large Language Models for Water Distribution Systems Modeling and Decision-Making

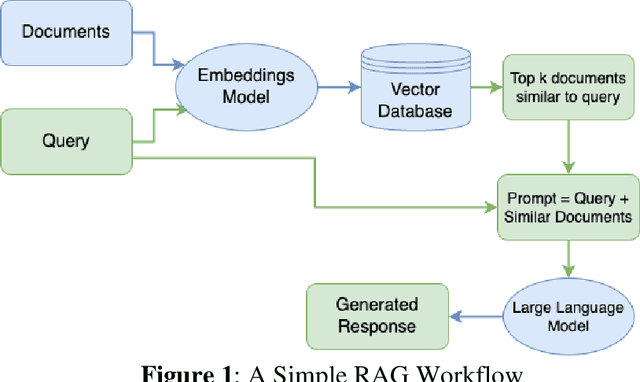
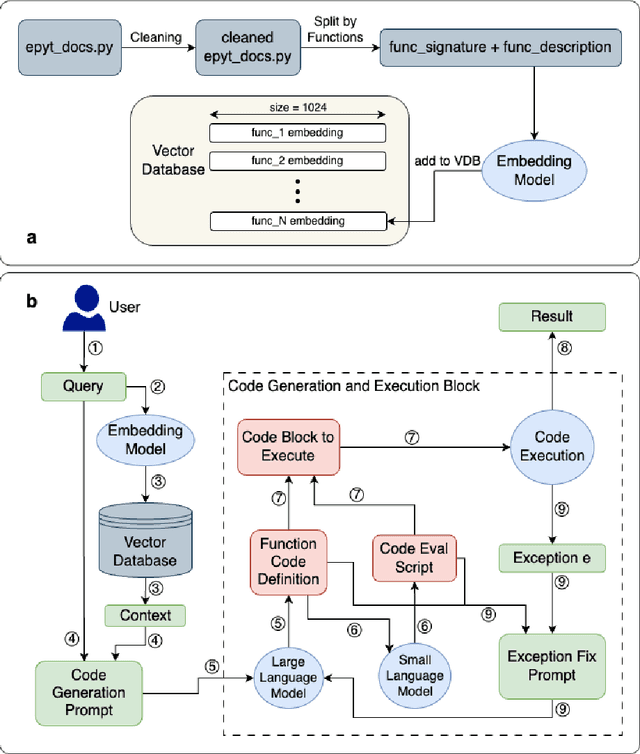
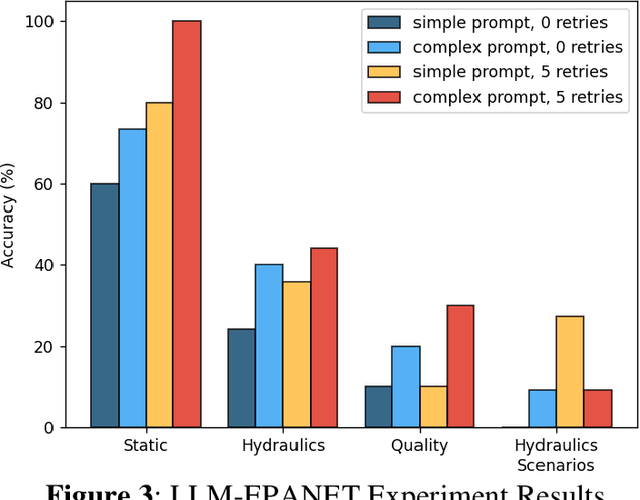
The design, operations, and management of water distribution systems (WDS) involve complex mathematical models. These models are continually improving due to computational advancements, leading to better decision-making and more efficient WDS management. However, the significant time and effort required for modeling, programming, and analyzing results remain substantial challenges. Another issue is the professional burden, which confines the interaction with models, databases, and other sophisticated tools to a small group of experts, thereby causing non-technical stakeholders to depend on these experts or make decisions without modeling support. Furthermore, explaining model results is challenging even for experts, as it is often unclear which conditions cause the model to reach a certain state or recommend a specific policy. The recent advancements in Large Language Models (LLMs) open doors for a new stage in human-model interaction. This study proposes a framework of plain language interactions with hydraulic and water quality models based on LLM-EPANET architecture. This framework is tested with increasing levels of complexity of queries to study the ability of LLMs to interact with WDS models, run complex simulations, and report simulation results. The performance of the proposed framework is evaluated across several categories of queries and hyper-parameter configurations, demonstrating its potential to enhance decision-making processes in WDS management.

CompAct: Compressed Activations for Memory-Efficient LLM Training

We introduce CompAct, a technique that reduces peak memory utilization on GPU by 25-30% for pretraining and 50% for fine-tuning of LLMs. Peak device memory is a major limiting factor in training LLMs, with various recent works aiming to reduce model memory. However most works don't target the largest component of allocated memory during training: the model's compute graph, which is stored for the backward pass. By storing low-rank, compressed activations to be used in the backward pass we greatly reduce the required memory, unlike previous methods which only reduce optimizer overheads or the number of trained parameters. Our compression uses random projection matrices, thus avoiding additional memory overheads. Comparisons with previous techniques for either pretraining or fine-tuning show that CompAct substantially improves existing compute-performance tradeoffs. We expect CompAct's savings to scale even higher for larger models.

DNCs Require More Planning Steps

Many recent works use machine learning models to solve various complex algorithmic problems. However, these models attempt to reach a solution without considering the problem's required computational complexity, which can be detrimental to their ability to solve it correctly. In this work we investigate the effect of computational time and memory on generalization of implicit algorithmic solvers. To do so, we focus on the Differentiable Neural Computer (DNC), a general problem solver that also lets us reason directly about its usage of time and memory. In this work, we argue that the number of planning steps the model is allowed to take, which we call "planning budget", is a constraint that can cause the model to generalize poorly and hurt its ability to fully utilize its external memory. We evaluate our method on Graph Shortest Path, Convex Hull, Graph MinCut and Associative Recall, and show how the planning budget can drastically change the behavior of the learned algorithm, in terms of learned time complexity, training time, stability and generalization to inputs larger than those seen during training.

Probabilistic Invariant Learning with Randomized Linear Classifiers

Designing models that are both expressive and preserve known invariances of tasks is an increasingly hard problem. Existing solutions tradeoff invariance for computational or memory resources. In this work, we show how to leverage randomness and design models that are both expressive and invariant but use less resources. Inspired by randomized algorithms, our key insight is that accepting probabilistic notions of universal approximation and invariance can reduce our resource requirements. More specifically, we propose a class of binary classification models called Randomized Linear Classifiers (RLCs). We give parameter and sample size conditions in which RLCs can, with high probability, approximate any (smooth) function while preserving invariance to compact group transformations. Leveraging this result, we design three RLCs that are provably probabilistic invariant for classification tasks over sets, graphs, and spherical data. We show how these models can achieve probabilistic invariance and universality using less resources than (deterministic) neural networks and their invariant counterparts. Finally, we empirically demonstrate the benefits of this new class of models on invariant tasks where deterministic invariant neural networks are known to struggle.

FOSI: Hybrid First and Second Order Optimization

Though second-order optimization methods are highly effective, popular approaches in machine learning such as SGD and Adam use only first-order information due to the difficulty of computing curvature in high dimensions. We present FOSI, a novel meta-algorithm that improves the performance of any first-order optimizer by efficiently incorporating second-order information during the optimization process. In each iteration, FOSI implicitly splits the function into two quadratic functions defined on orthogonal subspaces, then uses a second-order method to minimize the first, and the base optimizer to minimize the other. Our analysis of FOSI's preconditioner and effective Hessian proves that FOSI improves the condition number for a large family of optimizers. Our empirical evaluation demonstrates that FOSI improves the convergence rate and optimization time of GD, Heavy-Ball, and Adam when applied to several deep neural networks training tasks such as audio classification, transfer learning, and object classification and when applied to convex functions.

Unsupervised Frequent Pattern Mining for CEP

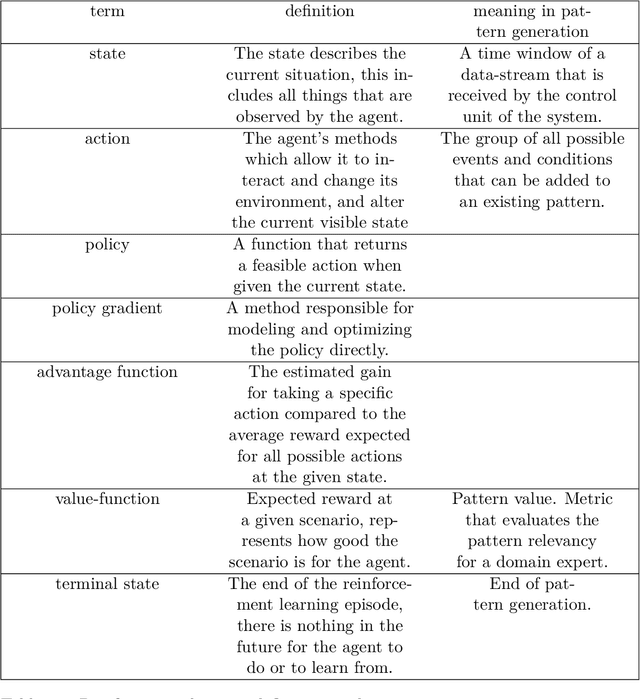
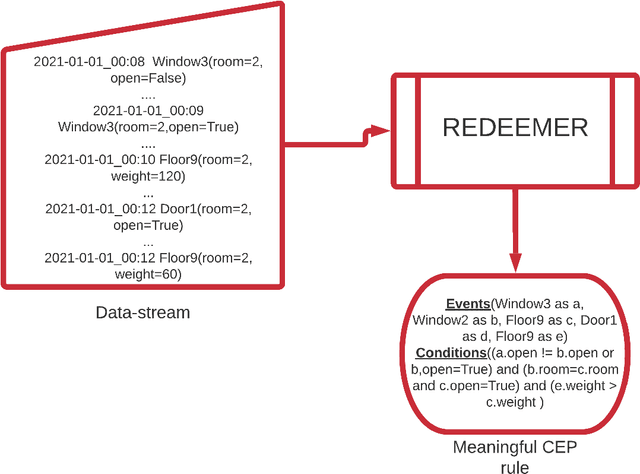
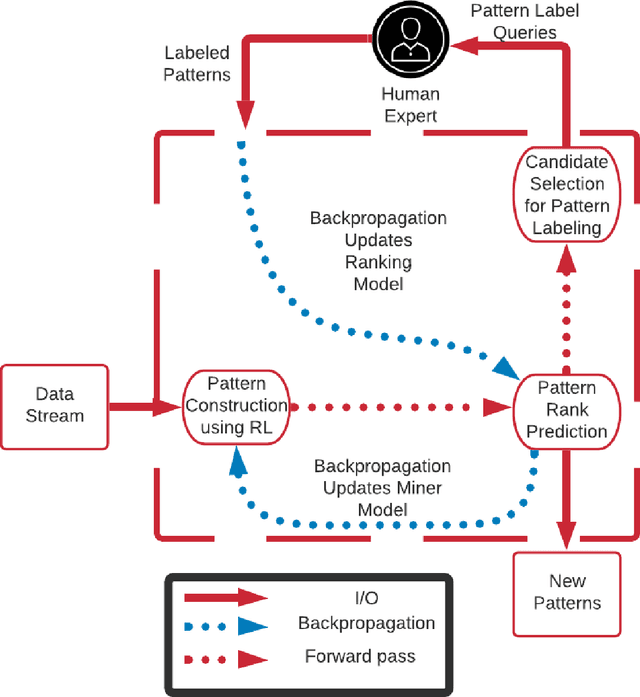
Complex Event Processing (CEP) is a set of methods that allow efficient knowledge extraction from massive data streams using complex and highly descriptive patterns. Numerous applications, such as online finance, healthcare monitoring and fraud detection use CEP technologies to capture critical alerts, potential threats, or vital notifications in real time. As of today, in many fields, patterns are manually defined by human experts. However, desired patterns often contain convoluted relations that are difficult for humans to detect, and human expertise is scarce in many domains. We present REDEEMER (REinforcement baseD cEp pattErn MinER), a novel reinforcement and active learning approach aimed at mining CEP patterns that allow expansion of the knowledge extracted while reducing the human effort required. This approach includes a novel policy gradient method for vast multivariate spaces and a new way to combine reinforcement and active learning for CEP rule learning while minimizing the number of labels needed for training. REDEEMER aims to enable CEP integration in domains that could not utilize it before. To the best of our knowledge, REDEEMER is the first system that suggests new CEP rules that were not observed beforehand, and is the first method aimed for increasing pattern knowledge in fields where experts do not possess sufficient information required for CEP tools. Our experiments on diverse data-sets demonstrate that REDEEMER is able to extend pattern knowledge while outperforming several state-of-the-art reinforcement learning methods for pattern mining.

Coin Flipping Neural Networks

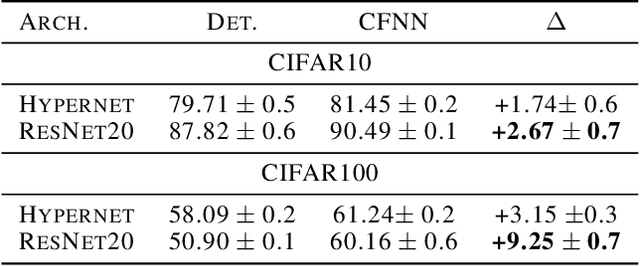
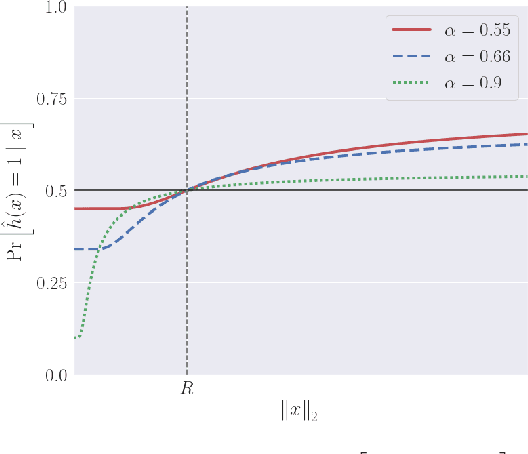
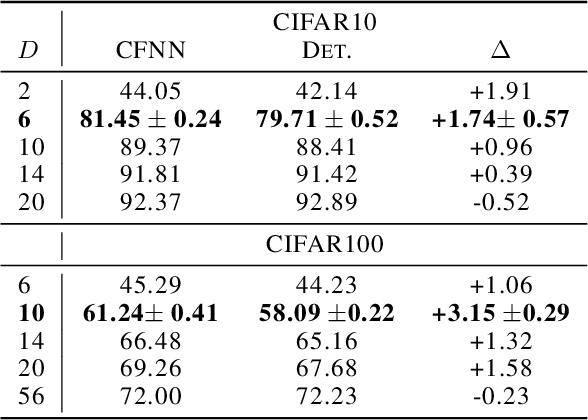
We show that neural networks with access to randomness can outperform deterministic networks by using amplification. We call such networks Coin-Flipping Neural Networks, or CFNNs. We show that a CFNN can approximate the indicator of a $d$-dimensional ball to arbitrary accuracy with only 2 layers and $\mathcal{O}(1)$ neurons, where a 2-layer deterministic network was shown to require $\Omega(e^d)$ neurons, an exponential improvement (arXiv:1610.09887). We prove a highly non-trivial result, that for almost any classification problem, there exists a trivially simple network that solves it given a sufficiently powerful generator for the network's weights. Combining these results we conjecture that for most classification problems, there is a CFNN which solves them with higher accuracy or fewer neurons than any deterministic network. Finally, we verify our proofs experimentally using novel CFNN architectures on CIFAR10 and CIFAR100, reaching an improvement of 9.25\% from the baseline.

Learning Under Delayed Feedback: Implicitly Adapting to Gradient Delays

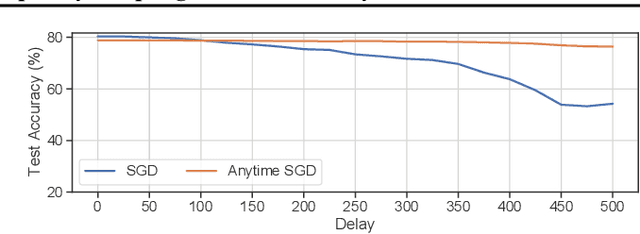
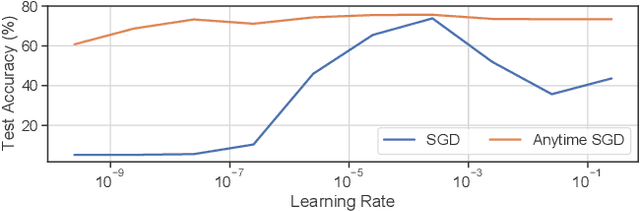
We consider stochastic convex optimization problems, where several machines act asynchronously in parallel while sharing a common memory. We propose a robust training method for the constrained setting and derive non asymptotic convergence guarantees that do not depend on prior knowledge of update delays, objective smoothness, and gradient variance. Conversely, existing methods for this setting crucially rely on this prior knowledge, which render them unsuitable for essentially all shared-resources computational environments, such as clouds and data centers. Concretely, existing approaches are unable to accommodate changes in the delays which result from dynamic allocation of the machines, while our method implicitly adapts to such changes.

It's Not What Machines Can Learn, It's What We Cannot Teach

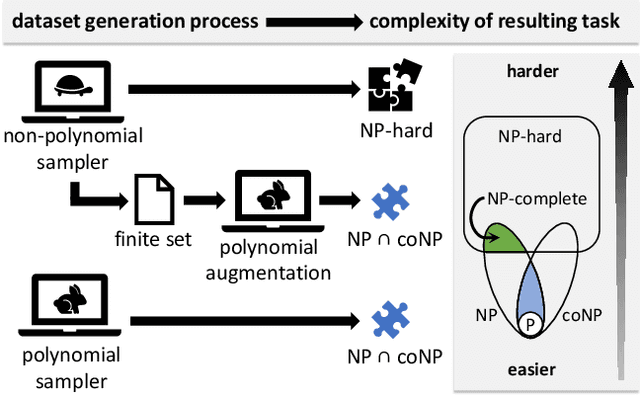
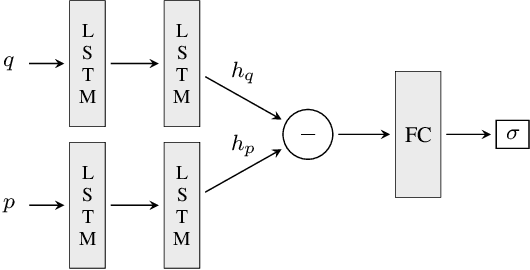
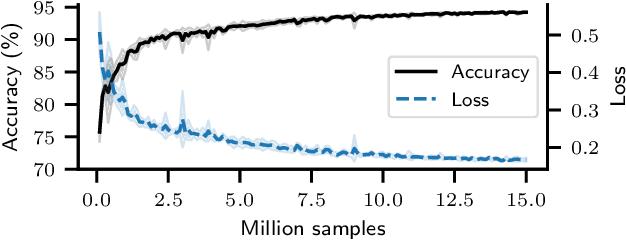
Can deep neural networks learn to solve any task, and in particular problems of high complexity? This question attracts a lot of interest, with recent works tackling computationally hard tasks such as the traveling salesman problem and satisfiability. In this work we offer a different perspective on this question. Given the common assumption that $\textit{NP} \neq \textit{coNP}$ we prove that any polynomial-time sample generator for an $\textit{NP}$-hard problem samples, in fact, from an easier sub-problem. We empirically explore a case study, Conjunctive Query Containment, and show how common data generation techniques generate biased datasets that lead practitioners to over-estimate model accuracy. Our results suggest that machine learning approaches that require training on a dense uniform sampling from the target distribution cannot be used to solve computationally hard problems, the reason being the difficulty of generating sufficiently large and unbiased training sets.

Adaptive Communication Bounds for Distributed Online Learning

We consider distributed online learning protocols that control the exchange of information between local learners in a round-based learning scenario. The learning performance of such a protocol is intuitively optimal if approximately the same loss is incurred as in a hypothetical serial setting. If a protocol accomplishes this, it is inherently impossible to achieve a strong communication bound at the same time. In the worst case, every input is essential for the learning performance, even for the serial setting, and thus needs to be exchanged between the local learners. However, it is reasonable to demand a bound that scales well with the hardness of the serialized prediction problem, as measured by the loss received by a serial online learning algorithm. We provide formal criteria based on this intuition and show that they hold for a simplified version of a previously published protocol.