DiT-Flow: Speech Enhancement Robust to Multiple Distortions based on Flow Matching in Latent Space and Diffusion Transformers

Recent advances in generative models, such as diffusion and flow matching, have shown strong performance in audio tasks. However, speech enhancement (SE) models are typically trained on limited datasets and evaluated under narrow conditions, limiting real-world applicability. To address this, we propose DiT-Flow, a flow matching-based SE framework built on the latent Diffusion Transformer (DiT) backbone and trained for robustness across diverse distortions, including noise, reverberation, and compression. DiT-Flow operates on compact variational auto-encoders (VAEs)-derived latent features. We validated our approach on StillSonicSet, a synthetic yet acoustically realistic dataset composed of LibriSpeech, FSD50K, FMA, and 90 Matterport3D scenes. Experiments show that DiT-Flow consistently outperforms state-of-the-art generative SE models, demonstrating the effectiveness of flow matching in multi-condition speech enhancement. Despite ongoing efforts to expand synthetic data realism, a persistent bottleneck in SE is the inevitable mismatch between training and deployment conditions. By integrating LoRA with the MoE framework, we achieve both parameter-efficient and high-performance training for DiT-Flow robust to multiple distortions with using 4.9% percentage of the total parameters to obtain a better performance on five unseen distortions.

CompAct: Compressed Activations for Memory-Efficient LLM Training

We introduce CompAct, a technique that reduces peak memory utilization on GPU by 25-30% for pretraining and 50% for fine-tuning of LLMs. Peak device memory is a major limiting factor in training LLMs, with various recent works aiming to reduce model memory. However most works don't target the largest component of allocated memory during training: the model's compute graph, which is stored for the backward pass. By storing low-rank, compressed activations to be used in the backward pass we greatly reduce the required memory, unlike previous methods which only reduce optimizer overheads or the number of trained parameters. Our compression uses random projection matrices, thus avoiding additional memory overheads. Comparisons with previous techniques for either pretraining or fine-tuning show that CompAct substantially improves existing compute-performance tradeoffs. We expect CompAct's savings to scale even higher for larger models.

DNCs Require More Planning Steps

Many recent works use machine learning models to solve various complex algorithmic problems. However, these models attempt to reach a solution without considering the problem's required computational complexity, which can be detrimental to their ability to solve it correctly. In this work we investigate the effect of computational time and memory on generalization of implicit algorithmic solvers. To do so, we focus on the Differentiable Neural Computer (DNC), a general problem solver that also lets us reason directly about its usage of time and memory. In this work, we argue that the number of planning steps the model is allowed to take, which we call "planning budget", is a constraint that can cause the model to generalize poorly and hurt its ability to fully utilize its external memory. We evaluate our method on Graph Shortest Path, Convex Hull, Graph MinCut and Associative Recall, and show how the planning budget can drastically change the behavior of the learned algorithm, in terms of learned time complexity, training time, stability and generalization to inputs larger than those seen during training.

Coin Flipping Neural Networks

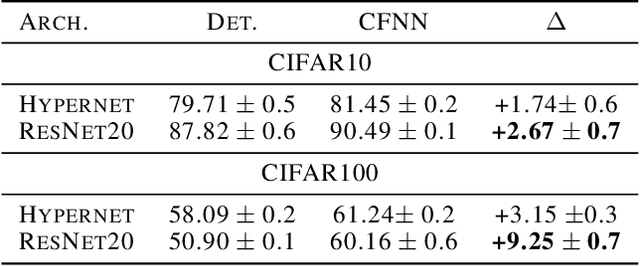
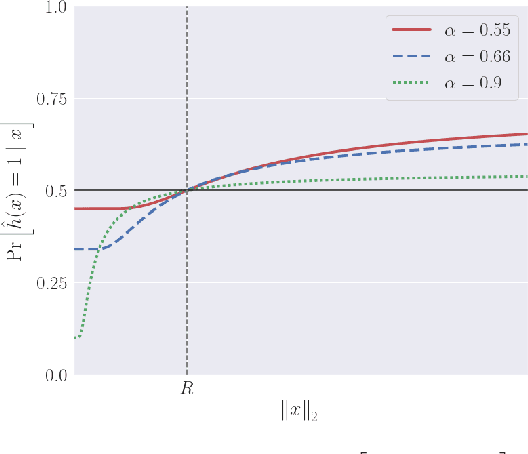
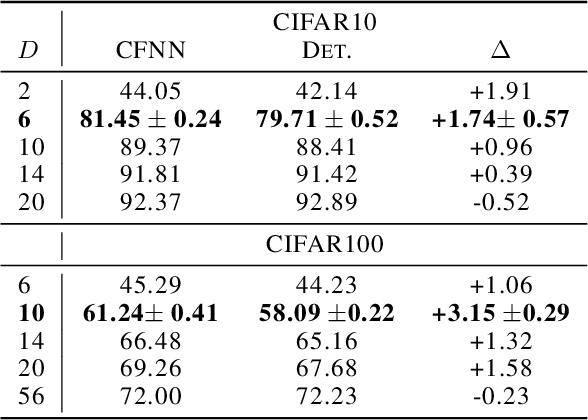
We show that neural networks with access to randomness can outperform deterministic networks by using amplification. We call such networks Coin-Flipping Neural Networks, or CFNNs. We show that a CFNN can approximate the indicator of a $d$-dimensional ball to arbitrary accuracy with only 2 layers and $\mathcal{O}(1)$ neurons, where a 2-layer deterministic network was shown to require $\Omega(e^d)$ neurons, an exponential improvement (arXiv:1610.09887). We prove a highly non-trivial result, that for almost any classification problem, there exists a trivially simple network that solves it given a sufficiently powerful generator for the network's weights. Combining these results we conjecture that for most classification problems, there is a CFNN which solves them with higher accuracy or fewer neurons than any deterministic network. Finally, we verify our proofs experimentally using novel CFNN architectures on CIFAR10 and CIFAR100, reaching an improvement of 9.25\% from the baseline.