Probabilistic Invariant Learning with Randomized Linear Classifiers

Designing models that are both expressive and preserve known invariances of tasks is an increasingly hard problem. Existing solutions tradeoff invariance for computational or memory resources. In this work, we show how to leverage randomness and design models that are both expressive and invariant but use less resources. Inspired by randomized algorithms, our key insight is that accepting probabilistic notions of universal approximation and invariance can reduce our resource requirements. More specifically, we propose a class of binary classification models called Randomized Linear Classifiers (RLCs). We give parameter and sample size conditions in which RLCs can, with high probability, approximate any (smooth) function while preserving invariance to compact group transformations. Leveraging this result, we design three RLCs that are provably probabilistic invariant for classification tasks over sets, graphs, and spherical data. We show how these models can achieve probabilistic invariance and universality using less resources than (deterministic) neural networks and their invariant counterparts. Finally, we empirically demonstrate the benefits of this new class of models on invariant tasks where deterministic invariant neural networks are known to struggle.

Coin Flipping Neural Networks

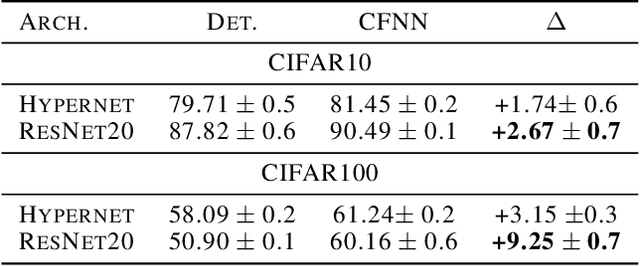
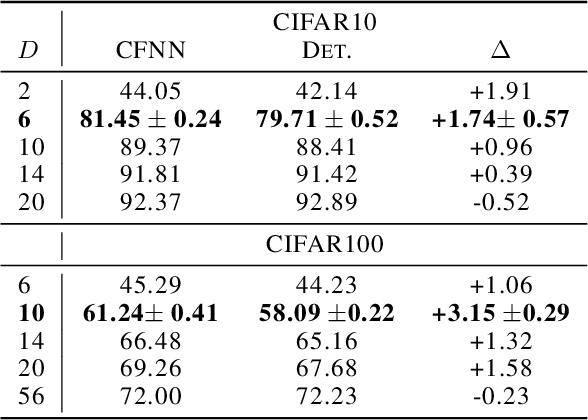
We show that neural networks with access to randomness can outperform deterministic networks by using amplification. We call such networks Coin-Flipping Neural Networks, or CFNNs. We show that a CFNN can approximate the indicator of a $d$-dimensional ball to arbitrary accuracy with only 2 layers and $\mathcal{O}(1)$ neurons, where a 2-layer deterministic network was shown to require $\Omega(e^d)$ neurons, an exponential improvement (arXiv:1610.09887). We prove a highly non-trivial result, that for almost any classification problem, there exists a trivially simple network that solves it given a sufficiently powerful generator for the network's weights. Combining these results we conjecture that for most classification problems, there is a CFNN which solves them with higher accuracy or fewer neurons than any deterministic network. Finally, we verify our proofs experimentally using novel CFNN architectures on CIFAR10 and CIFAR100, reaching an improvement of 9.25\% from the baseline.

Slicing the hypercube is not easy

We prove that at least $\Omega(n^{0.51})$ hyperplanes are needed to slice all edges of the $n$-dimensional hypercube. We provide a couple of applications: lower bounds on the computational complexity of parity, and a lower bound on the cover number of the hypercube by skew hyperplanes.

It's Not What Machines Can Learn, It's What We Cannot Teach

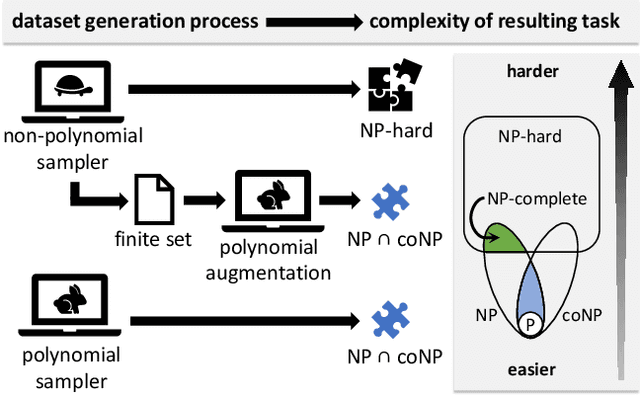
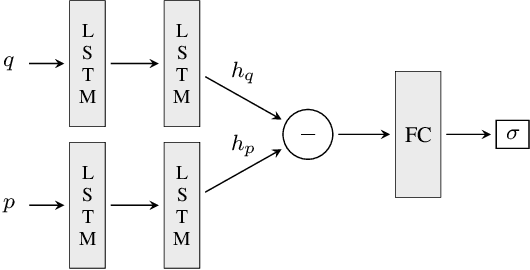
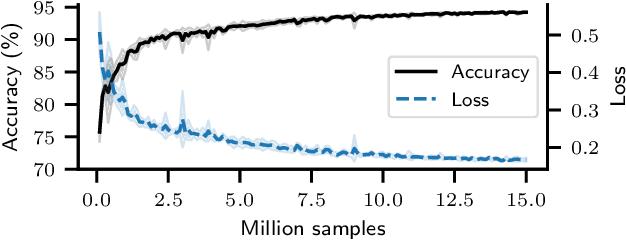
Can deep neural networks learn to solve any task, and in particular problems of high complexity? This question attracts a lot of interest, with recent works tackling computationally hard tasks such as the traveling salesman problem and satisfiability. In this work we offer a different perspective on this question. Given the common assumption that $\textit{NP} \neq \textit{coNP}$ we prove that any polynomial-time sample generator for an $\textit{NP}$-hard problem samples, in fact, from an easier sub-problem. We empirically explore a case study, Conjunctive Query Containment, and show how common data generation techniques generate biased datasets that lead practitioners to over-estimate model accuracy. Our results suggest that machine learning approaches that require training on a dense uniform sampling from the target distribution cannot be used to solve computationally hard problems, the reason being the difficulty of generating sufficiently large and unbiased training sets.