FOSI: Hybrid First and Second Order Optimization

Though second-order optimization methods are highly effective, popular approaches in machine learning such as SGD and Adam use only first-order information due to the difficulty of computing curvature in high dimensions. We present FOSI, a novel meta-algorithm that improves the performance of any first-order optimizer by efficiently incorporating second-order information during the optimization process. In each iteration, FOSI implicitly splits the function into two quadratic functions defined on orthogonal subspaces, then uses a second-order method to minimize the first, and the base optimizer to minimize the other. Our analysis of FOSI's preconditioner and effective Hessian proves that FOSI improves the condition number for a large family of optimizers. Our empirical evaluation demonstrates that FOSI improves the convergence rate and optimization time of GD, Heavy-Ball, and Adam when applied to several deep neural networks training tasks such as audio classification, transfer learning, and object classification and when applied to convex functions.

Optimizing Data Collection in Deep Reinforcement Learning

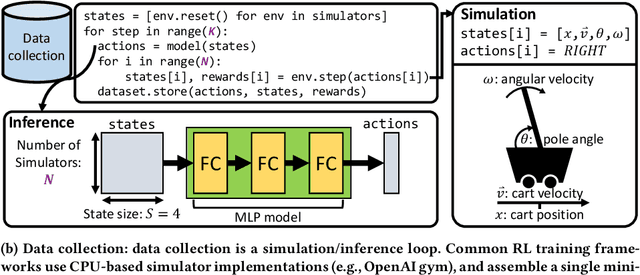
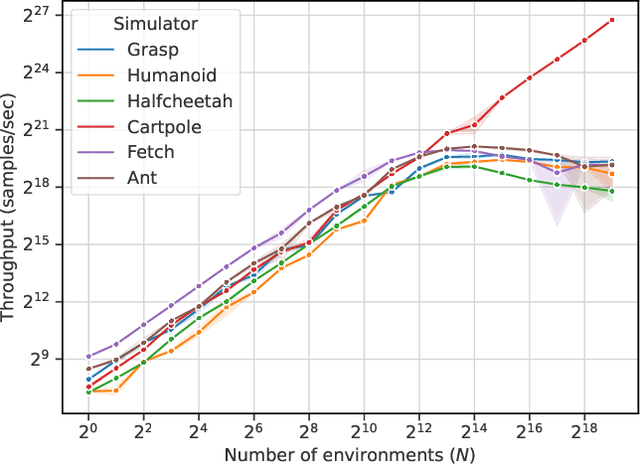
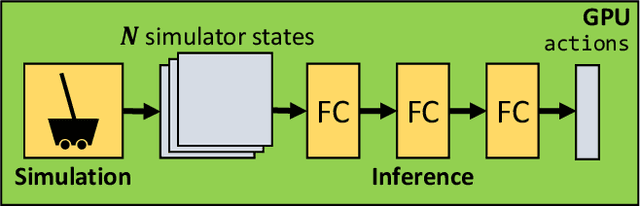
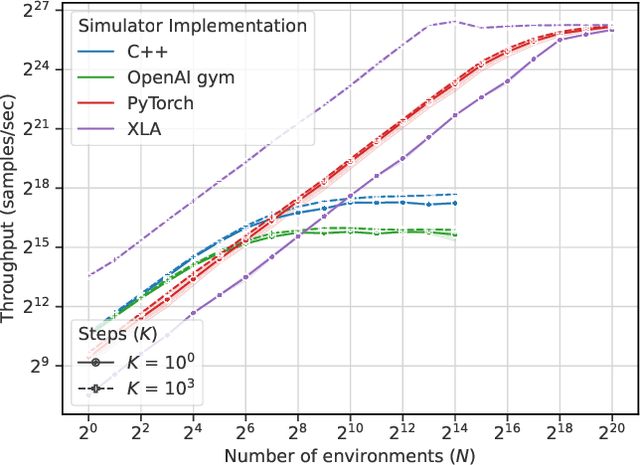
Reinforcement learning (RL) workloads take a notoriously long time to train due to the large number of samples collected at run-time from simulators. Unfortunately, cluster scale-up approaches remain expensive, and commonly used CPU implementations of simulators induce high overhead when switching back and forth between GPU computations. We explore two optimizations that increase RL data collection efficiency by increasing GPU utilization: (1) GPU vectorization: parallelizing simulation on the GPU for increased hardware parallelism, and (2) simulator kernel fusion: fusing multiple simulation steps to run in a single GPU kernel launch to reduce global memory bandwidth requirements. We find that GPU vectorization can achieve up to $1024\times$ speedup over commonly used CPU simulators. We profile the performance of different implementations and show that for a simple simulator, ML compiler implementations (XLA) of GPU vectorization outperform a DNN framework (PyTorch) by $13.4\times$ by reducing CPU overhead from repeated Python to DL backend API calls. We show that simulator kernel fusion speedups with a simple simulator are $11.3\times$ and increase by up to $1024\times$ as simulator complexity increases in terms of memory bandwidth requirements. We show that the speedups from simulator kernel fusion are orthogonal and combinable with GPU vectorization, leading to a multiplicative speedup.

RL-Scope: Cross-Stack Profiling for Deep Reinforcement Learning Workloads

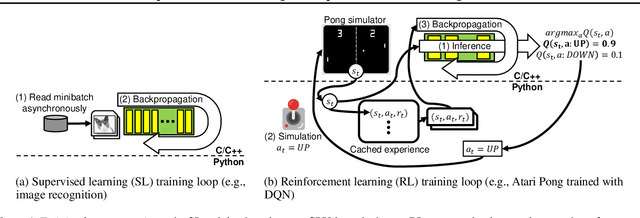
Deep reinforcement learning (RL) has made groundbreaking advancements in robotics, data center management and other applications. Unfortunately, system-level bottlenecks in RL workloads are poorly understood; we observe fundamental structural differences in RL workloads that make them inherently less GPU-bound than supervised learning (SL). To explain where training time is spent in RL workloads, we propose RL-Scope, a cross-stack profiler that scopes low-level CPU/GPU resource usage to high-level algorithmic operations, and provides accurate insights by correcting for profiling overhead. Using RL-Scope, we survey RL workloads across its major dimensions including ML backend, RL algorithm, and simulator. For ML backends, we explain a $2.3\times$ difference in runtime between equivalent PyTorch and TensorFlow algorithm implementations, and identify a bottleneck rooted in overly abstracted algorithm implementations. For RL algorithms and simulators, we show that on-policy algorithms are at least $3.5\times$ more simulation-bound than off-policy algorithms. Finally, we profile a scale-up workload and demonstrate that GPU utilization metrics reported by commonly used tools dramatically inflate GPU usage, whereas RL-Scope reports true GPU-bound time. RL-Scope is an open-source tool available at https://github.com/UofT-EcoSystem/rlscope .

It's Not What Machines Can Learn, It's What We Cannot Teach

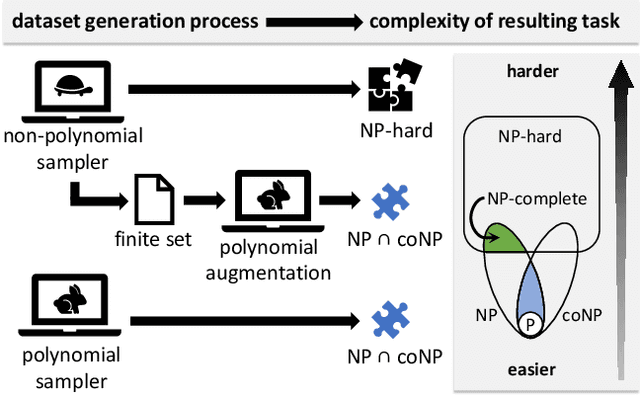
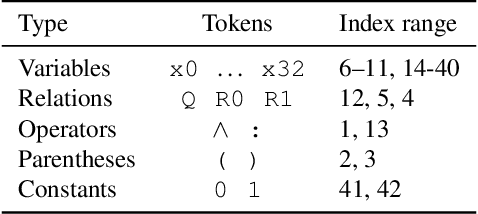
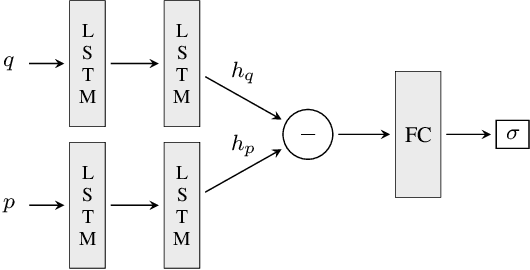
Can deep neural networks learn to solve any task, and in particular problems of high complexity? This question attracts a lot of interest, with recent works tackling computationally hard tasks such as the traveling salesman problem and satisfiability. In this work we offer a different perspective on this question. Given the common assumption that $\textit{NP} \neq \textit{coNP}$ we prove that any polynomial-time sample generator for an $\textit{NP}$-hard problem samples, in fact, from an easier sub-problem. We empirically explore a case study, Conjunctive Query Containment, and show how common data generation techniques generate biased datasets that lead practitioners to over-estimate model accuracy. Our results suggest that machine learning approaches that require training on a dense uniform sampling from the target distribution cannot be used to solve computationally hard problems, the reason being the difficulty of generating sufficiently large and unbiased training sets.

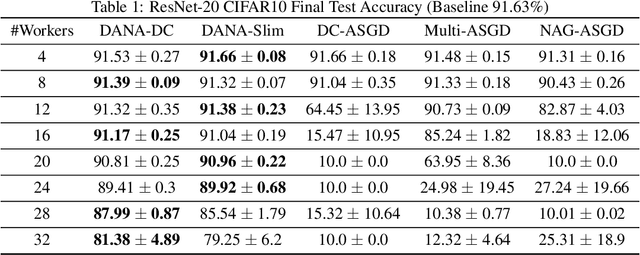
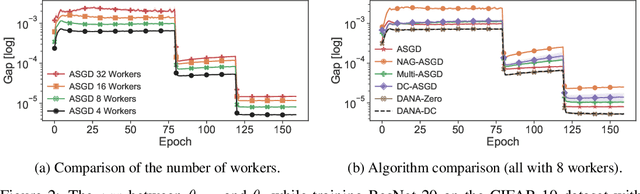
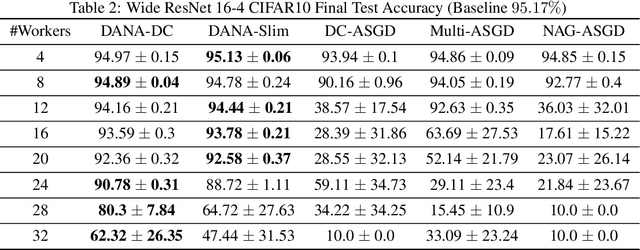
Taming Momentum in a Distributed Asynchronous Environment

Although distributed computing can significantly reduce the training time of deep neural networks, scaling the training process while maintaining high efficiency and final accuracy is challenging. Distributed asynchronous training enjoys near-linear speedup, but asynchrony causes gradient staleness, the main difficulty in scaling stochastic gradient descent to large clusters. Momentum, which is often used to accelerate convergence and escape local minima, exacerbates the gradient staleness, thereby hindering convergence. We propose DANA: a novel asynchronous distributed technique which is based on a new gradient staleness measure that we call the gap. By minimizing the gap, DANA mitigates the gradient staleness, despite using momentum, and therefore scales to large clusters while maintaining high final accuracy and fast convergence. DANA adapts Nesterov's Accelerated Gradient to a distributed setting, computing the gradient on an estimated future position of the model's parameters. In turn, we show that DANA's estimation of the future position amplifies the use of a Taylor expansion, which relies on a fast Hessian approximation, making it much more effective and accurate. Our evaluation on the CIFAR and ImageNet datasets shows that DANA outperforms existing methods, in both final accuracy and convergence speed.