Gap Aware Mitigation of Gradient Staleness

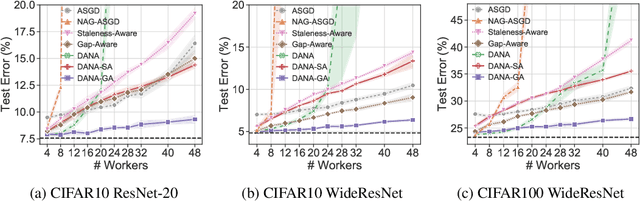
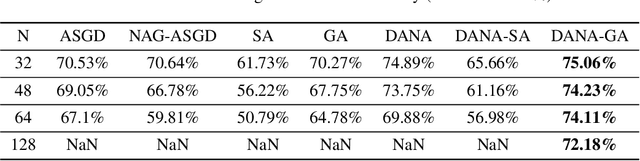
Cloud computing is becoming increasingly popular as a platform for distributed training of deep neural networks. Synchronous stochastic gradient descent (SSGD) suffers from substantial slowdowns due to stragglers if the environment is non-dedicated, as is common in cloud computing. Asynchronous SGD (ASGD) methods are immune to these slowdowns but are scarcely used due to gradient staleness, which encumbers the convergence process. Recent techniques have had limited success mitigating the gradient staleness when scaling up to many workers (computing nodes). In this paper we define the Gap as a measure of gradient staleness and propose Gap-Aware (GA), a novel asynchronous-distributed method that penalizes stale gradients linearly to the Gap and performs well even when scaling to large numbers of workers. Our evaluation on the CIFAR, ImageNet, and WikiText-103 datasets shows that GA outperforms the currently acceptable gradient penalization method, in final test accuracy. We also provide convergence rate proof for GA. Despite prior beliefs, we show that if GA is applied, momentum becomes beneficial in asynchronous environments, even when the number of workers scales up.

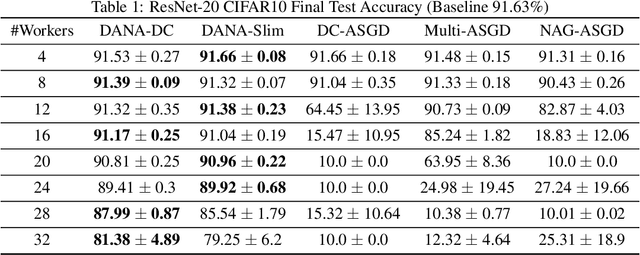
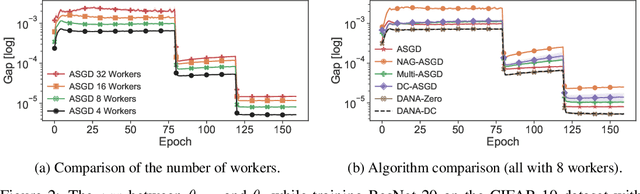
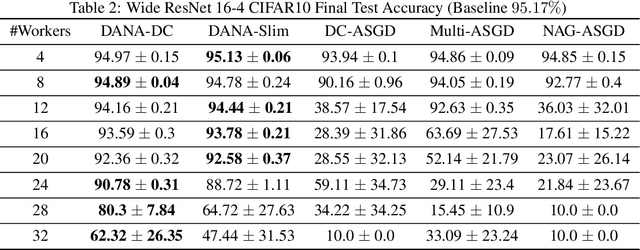
Taming Momentum in a Distributed Asynchronous Environment

Although distributed computing can significantly reduce the training time of deep neural networks, scaling the training process while maintaining high efficiency and final accuracy is challenging. Distributed asynchronous training enjoys near-linear speedup, but asynchrony causes gradient staleness, the main difficulty in scaling stochastic gradient descent to large clusters. Momentum, which is often used to accelerate convergence and escape local minima, exacerbates the gradient staleness, thereby hindering convergence. We propose DANA: a novel asynchronous distributed technique which is based on a new gradient staleness measure that we call the gap. By minimizing the gap, DANA mitigates the gradient staleness, despite using momentum, and therefore scales to large clusters while maintaining high final accuracy and fast convergence. DANA adapts Nesterov's Accelerated Gradient to a distributed setting, computing the gradient on an estimated future position of the model's parameters. In turn, we show that DANA's estimation of the future position amplifies the use of a Taylor expansion, which relies on a fast Hessian approximation, making it much more effective and accurate. Our evaluation on the CIFAR and ImageNet datasets shows that DANA outperforms existing methods, in both final accuracy and convergence speed.