Amir Yehudayoff
Approximation Depth of Convex Polytopes
Jul 10, 2025Abstract:We study approximations of polytopes in the standard model for computing polytopes using Minkowski sums and (convex hulls of) unions. Specifically, we study the ability to approximate a target polytope by polytopes of a given depth. Our main results imply that simplices can only be ``trivially approximated''. On the way, we obtain a characterization of simplices as the only ``outer additive'' convex bodies.
Better Neural Network Expressivity: Subdividing the Simplex
May 20, 2025Abstract:This work studies the expressivity of ReLU neural networks with a focus on their depth. A sequence of previous works showed that $\lceil \log_2(n+1) \rceil$ hidden layers are sufficient to compute all continuous piecewise linear (CPWL) functions on $\mathbb{R}^n$. Hertrich, Basu, Di Summa, and Skutella (NeurIPS'21) conjectured that this result is optimal in the sense that there are CPWL functions on $\mathbb{R}^n$, like the maximum function, that require this depth. We disprove the conjecture and show that $\lceil\log_3(n-1)\rceil+1$ hidden layers are sufficient to compute all CPWL functions on $\mathbb{R}^n$. A key step in the proof is that ReLU neural networks with two hidden layers can exactly represent the maximum function of five inputs. More generally, we show that $\lceil\log_3(n-2)\rceil+1$ hidden layers are sufficient to compute the maximum of $n\geq 4$ numbers. Our constructions almost match the $\lceil\log_3(n)\rceil$ lower bound of Averkov, Hojny, and Merkert (ICLR'25) in the special case of ReLU networks with weights that are decimal fractions. The constructions have a geometric interpretation via polyhedral subdivisions of the simplex into ``easier'' polytopes.
On the Depth of Monotone ReLU Neural Networks and ICNNs
May 09, 2025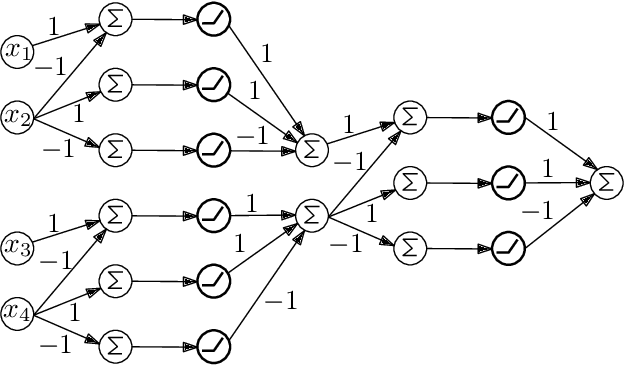
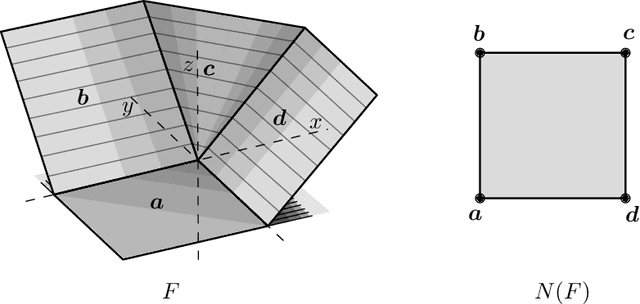
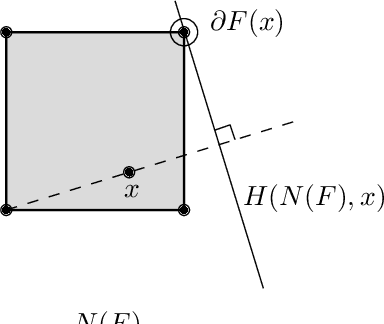
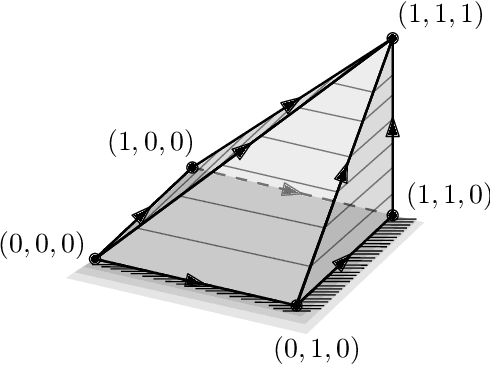
Abstract:We study two models of ReLU neural networks: monotone networks (ReLU$^+$) and input convex neural networks (ICNN). Our focus is on expressivity, mostly in terms of depth, and we prove the following lower bounds. For the maximum function MAX$_n$ computing the maximum of $n$ real numbers, we show that ReLU$^+$ networks cannot compute MAX$_n$, or even approximate it. We prove a sharp $n$ lower bound on the ICNN depth complexity of MAX$_n$. We also prove depth separations between ReLU networks and ICNNs; for every $k$, there is a depth-2 ReLU network of size $O(k^2)$ that cannot be simulated by a depth-$k$ ICNN. The proofs are based on deep connections between neural networks and polyhedral geometry, and also use isoperimetric properties of triangulations.
Data Selection for ERMs
Apr 20, 2025Abstract:Learning theory has traditionally followed a model-centric approach, focusing on designing optimal algorithms for a fixed natural learning task (e.g., linear classification or regression). In this paper, we adopt a complementary data-centric perspective, whereby we fix a natural learning rule and focus on optimizing the training data. Specifically, we study the following question: given a learning rule $\mathcal{A}$ and a data selection budget $n$, how well can $\mathcal{A}$ perform when trained on at most $n$ data points selected from a population of $N$ points? We investigate when it is possible to select $n \ll N$ points and achieve performance comparable to training on the entire population. We address this question across a variety of empirical risk minimizers. Our results include optimal data-selection bounds for mean estimation, linear classification, and linear regression. Additionally, we establish two general results: a taxonomy of error rates in binary classification and in stochastic convex optimization. Finally, we propose several open questions and directions for future research.
Dual VC Dimension Obstructs Sample Compression by Embeddings
May 27, 2024



Abstract:This work studies embedding of arbitrary VC classes in well-behaved VC classes, focusing particularly on extremal classes. Our main result expresses an impossibility: such embeddings necessarily require a significant increase in dimension. In particular, we prove that for every $d$ there is a class with VC dimension $d$ that cannot be embedded in any extremal class of VC dimension smaller than exponential in $d$. In addition to its independent interest, this result has an important implication in learning theory, as it reveals a fundamental limitation of one of the most extensively studied approaches to tackling the long-standing sample compression conjecture. Concretely, the approach proposed by Floyd and Warmuth entails embedding any given VC class into an extremal class of a comparable dimension, and then applying an optimal sample compression scheme for extremal classes. However, our results imply that this strategy would in some cases result in a sample compression scheme at least exponentially larger than what is predicted by the sample compression conjecture. The above implications follow from a general result we prove: any extremal class with VC dimension $d$ has dual VC dimension at most $2d+1$. This bound is exponentially smaller than the classical bound $2^{d+1}-1$ of Assouad, which applies to general concept classes (and is known to be unimprovable for some classes). We in fact prove a stronger result, establishing that $2d+1$ upper bounds the dual Radon number of extremal classes. This theorem represents an abstraction of the classical Radon theorem for convex sets, extending its applicability to a wider combinatorial framework, without relying on the specifics of Euclidean convexity. The proof utilizes the topological method and is primarily based on variants of the Topological Radon Theorem.
The Sample Complexity Of ERMs In Stochastic Convex Optimization
Nov 09, 2023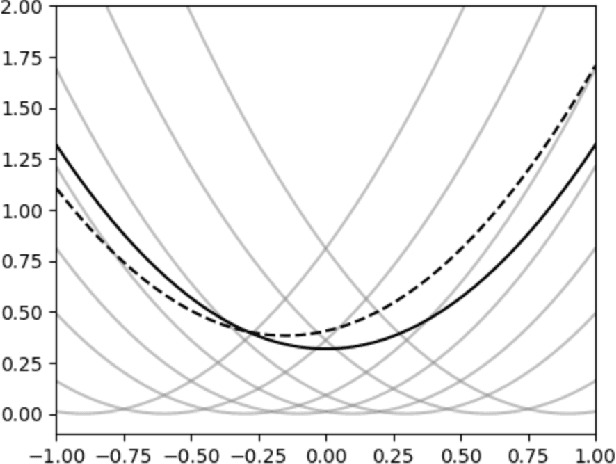
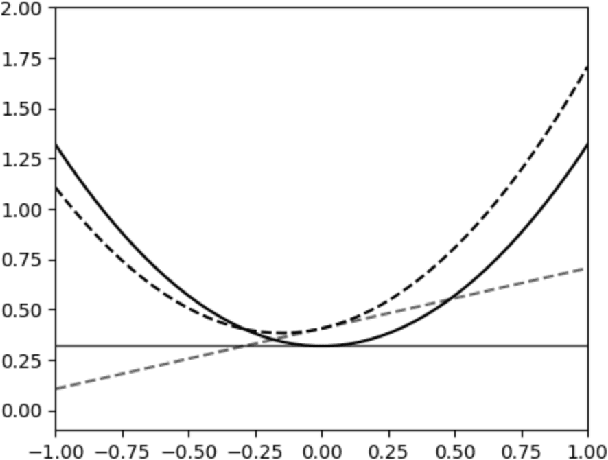
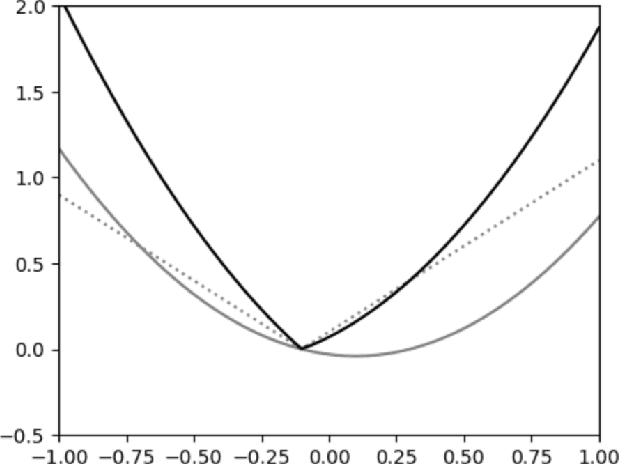
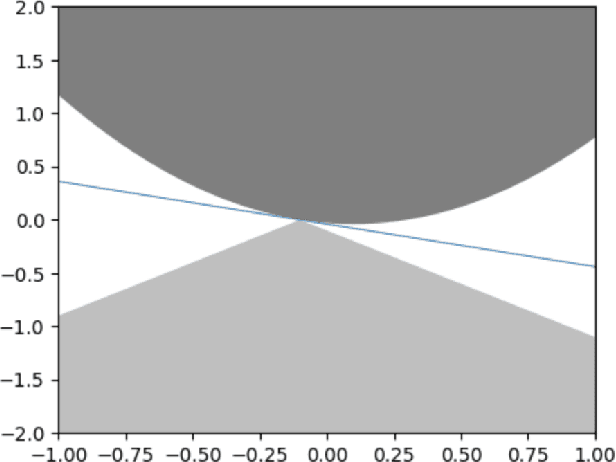
Abstract:Stochastic convex optimization is one of the most well-studied models for learning in modern machine learning. Nevertheless, a central fundamental question in this setup remained unresolved: "How many data points must be observed so that any empirical risk minimizer (ERM) shows good performance on the true population?" This question was proposed by Feldman (2016), who proved that $\Omega(\frac{d}{\epsilon}+\frac{1}{\epsilon^2})$ data points are necessary (where $d$ is the dimension and $\epsilon>0$ is the accuracy parameter). Proving an $\omega(\frac{d}{\epsilon}+\frac{1}{\epsilon^2})$ lower bound was left as an open problem. In this work we show that in fact $\tilde{O}(\frac{d}{\epsilon}+\frac{1}{\epsilon^2})$ data points are also sufficient. This settles the question and yields a new separation between ERMs and uniform convergence. This sample complexity holds for the classical setup of learning bounded convex Lipschitz functions over the Euclidean unit ball. We further generalize the result and show that a similar upper bound holds for all symmetric convex bodies. The general bound is composed of two terms: (i) a term of the form $\tilde{O}(\frac{d}{\epsilon})$ with an inverse-linear dependence on the accuracy parameter, and (ii) a term that depends on the statistical complexity of the class of $\textit{linear}$ functions (captured by the Rademacher complexity). The proof builds a mechanism for controlling the behavior of stochastic convex optimization problems.
Local Borsuk-Ulam, Stability, and Replicability
Nov 02, 2023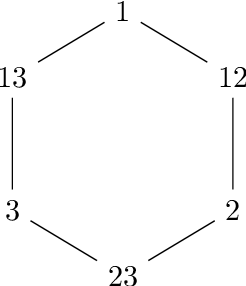
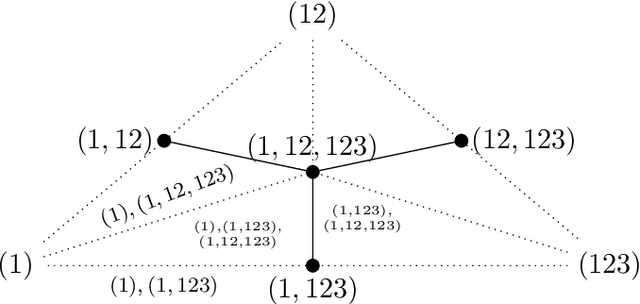
Abstract:We use and adapt the Borsuk-Ulam Theorem from topology to derive limitations on list-replicable and globally stable learning algorithms. We further demonstrate the applicability of our methods in combinatorics and topology. We show that, besides trivial cases, both list-replicable and globally stable learning are impossible in the agnostic PAC setting. This is in contrast with the realizable case where it is known that any class with a finite Littlestone dimension can be learned by such algorithms. In the realizable PAC setting, we sharpen previous impossibility results and broaden their scope. Specifically, we establish optimal bounds for list replicability and global stability numbers in finite classes. This provides an exponential improvement over previous works and implies an exponential separation from the Littlestone dimension. We further introduce lower bounds for weak learners, i.e., learners that are only marginally better than random guessing. Lower bounds from previous works apply only to stronger learners. To offer a broader and more comprehensive view of our topological approach, we prove a local variant of the Borsuk-Ulam theorem in topology and a result in combinatorics concerning Kneser colorings. In combinatorics, we prove that if $c$ is a coloring of all non-empty subsets of $[n]$ such that disjoint sets have different colors, then there is a chain of subsets that receives at least $1+ \lfloor n/2\rfloor$ colors (this bound is sharp). In topology, we prove e.g. that for any open antipodal-free cover of the $d$-dimensional sphere, there is a point $x$ that belongs to at least $t=\lceil\frac{d+3}{2}\rceil$ sets.
Replicability and stability in learning
Apr 12, 2023Abstract:Replicability is essential in science as it allows us to validate and verify research findings. Impagliazzo, Lei, Pitassi and Sorrell (`22) recently initiated the study of replicability in machine learning. A learning algorithm is replicable if it typically produces the same output when applied on two i.i.d. inputs using the same internal randomness. We study a variant of replicability that does not involve fixing the randomness. An algorithm satisfies this form of replicability if it typically produces the same output when applied on two i.i.d. inputs (without fixing the internal randomness). This variant is called global stability and was introduced by Bun, Livni and Moran ('20) in the context of differential privacy. Impagliazzo et al. showed how to boost any replicable algorithm so that it produces the same output with probability arbitrarily close to 1. In contrast, we demonstrate that for numerous learning tasks, global stability can only be accomplished weakly, where the same output is produced only with probability bounded away from 1. To overcome this limitation, we introduce the concept of list replicability, which is equivalent to global stability. Moreover, we prove that list replicability can be boosted so that it is achieved with probability arbitrarily close to 1. We also describe basic relations between standard learning-theoretic complexity measures and list replicable numbers. Our results, in addition, imply that besides trivial cases, replicable algorithms (in the sense of Impagliazzo et al.) must be randomized. The proof of the impossibility result is based on a topological fixed-point theorem. For every algorithm, we are able to locate a "hard input distribution" by applying the Poincar\'{e}-Miranda theorem in a related topological setting. The equivalence between global stability and list replicability is algorithmic.
A Unified Characterization of Private Learnability via Graph Theory
Apr 08, 2023Abstract:We provide a unified framework for characterizing pure and approximate differentially private (DP) learnabiliity. The framework uses the language of graph theory: for a concept class $\mathcal{H}$, we define the contradiction graph $G$ of $\mathcal{H}$. It vertices are realizable datasets, and two datasets $S,S'$ are connected by an edge if they contradict each other (i.e., there is a point $x$ that is labeled differently in $S$ and $S'$). Our main finding is that the combinatorial structure of $G$ is deeply related to learning $\mathcal{H}$ under DP. Learning $\mathcal{H}$ under pure DP is captured by the fractional clique number of $G$. Learning $\mathcal{H}$ under approximate DP is captured by the clique number of $G$. Consequently, we identify graph-theoretic dimensions that characterize DP learnability: the clique dimension and fractional clique dimension. Along the way, we reveal properties of the contradiction graph which may be of independent interest. We also suggest several open questions and directions for future research.
A Characterization of Multiclass Learnability
Mar 03, 2022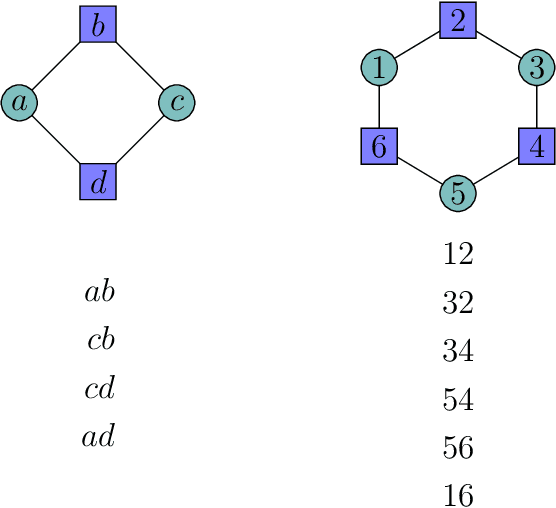
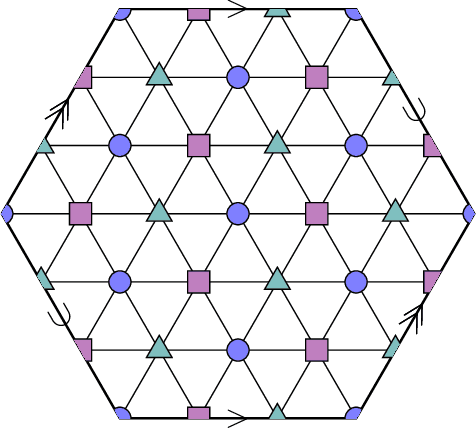
Abstract:A seminal result in learning theory characterizes the PAC learnability of binary classes through the Vapnik-Chervonenkis dimension. Extending this characterization to the general multiclass setting has been open since the pioneering works on multiclass PAC learning in the late 1980s. This work resolves this problem: we characterize multiclass PAC learnability through the DS dimension, a combinatorial dimension defined by Daniely and Shalev-Shwartz (2014). The classical characterization of the binary case boils down to empirical risk minimization. In contrast, our characterization of the multiclass case involves a variety of algorithmic ideas; these include a natural setting we call list PAC learning. In the list learning setting, instead of predicting a single outcome for a given unseen input, the goal is to provide a short menu of predictions. Our second main result concerns the Natarajan dimension, which has been a central candidate for characterizing multiclass learnability. This dimension was introduced by Natarajan (1988) as a barrier for PAC learning. Whether the Natarajan dimension characterizes PAC learnability in general has been posed as an open question in several papers since. This work provides a negative answer: we construct a non-learnable class with Natarajan dimension one. For the construction, we identify a fundamental connection between concept classes and topology (i.e., colorful simplicial complexes). We crucially rely on a deep and involved construction of hyperbolic pseudo-manifolds by Januszkiewicz and Swiatkowski. It is interesting that hyperbolicity is directly related to learning problems that are difficult to solve although no obvious barriers exist. This is another demonstration of the fruitful links machine learning has with different areas in mathematics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge