Not Every Image is Worth a Thousand Words: Quantifying Originality in Stable Diffusion

This work addresses the challenge of quantifying originality in text-to-image (T2I) generative diffusion models, with a focus on copyright originality. We begin by evaluating T2I models' ability to innovate and generalize through controlled experiments, revealing that stable diffusion models can effectively recreate unseen elements with sufficiently diverse training data. Then, our key insight is that concepts and combinations of image elements the model is familiar with, and saw more during training, are more concisly represented in the model's latent space. We hence propose a method that leverages textual inversion to measure the originality of an image based on the number of tokens required for its reconstruction by the model. Our approach is inspired by legal definitions of originality and aims to assess whether a model can produce original content without relying on specific prompts or having the training data of the model. We demonstrate our method using both a pre-trained stable diffusion model and a synthetic dataset, showing a correlation between the number of tokens and image originality. This work contributes to the understanding of originality in generative models and has implications for copyright infringement cases.

Credit Attribution and Stable Compression

Credit attribution is crucial across various fields. In academic research, proper citation acknowledges prior work and establishes original contributions. Similarly, in generative models, such as those trained on existing artworks or music, it is important to ensure that any generated content influenced by these works appropriately credits the original creators. We study credit attribution by machine learning algorithms. We propose new definitions--relaxations of Differential Privacy--that weaken the stability guarantees for a designated subset of $k$ datapoints. These $k$ datapoints can be used non-stably with permission from their owners, potentially in exchange for compensation. Meanwhile, the remaining datapoints are guaranteed to have no significant influence on the algorithm's output. Our framework extends well-studied notions of stability, including Differential Privacy ($k = 0$), differentially private learning with public data (where the $k$ public datapoints are fixed in advance), and stable sample compression (where the $k$ datapoints are selected adaptively by the algorithm). We examine the expressive power of these stability notions within the PAC learning framework, provide a comprehensive characterization of learnability for algorithms adhering to these principles, and propose directions and questions for future research.

The Sample Complexity of Gradient Descent in Stochastic Convex Optimization

We analyze the sample complexity of full-batch Gradient Descent (GD) in the setup of non-smooth Stochastic Convex Optimization. We show that the generalization error of GD, with common choice of hyper-parameters, can be $\tilde \Theta(d/m + 1/\sqrt{m})$, where $d$ is the dimension and $m$ is the sample size. This matches the sample complexity of \emph{worst-case} empirical risk minimizers. That means that, in contrast with other algorithms, GD has no advantage over naive ERMs. Our bound follows from a new generalization bound that depends on both the dimension as well as the learning rate and number of iterations. Our bound also shows that, for general hyper-parameters, when the dimension is strictly larger than number of samples, $T=\Omega(1/\epsilon^4)$ iterations are necessary to avoid overfitting. This resolves an open problem by Schlisserman et al.23 and Amir er Al.21, and improves over previous lower bounds that demonstrated that the sample size must be at least square root of the dimension.

Not All Similarities Are Created Equal: Leveraging Data-Driven Biases to Inform GenAI Copyright Disputes

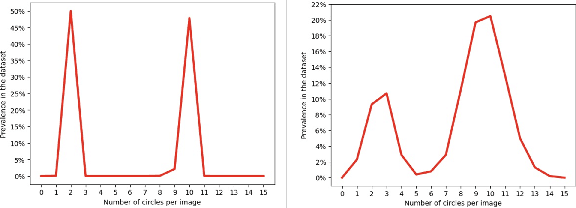
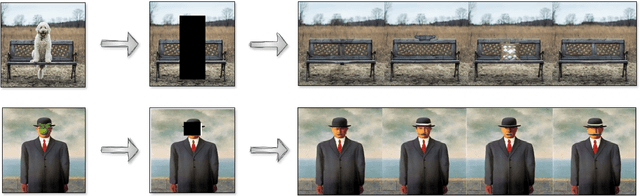
The advent of Generative Artificial Intelligence (GenAI) models, including GitHub Copilot, OpenAI GPT, and Stable Diffusion, has revolutionized content creation, enabling non-professionals to produce high-quality content across various domains. This transformative technology has led to a surge of synthetic content and sparked legal disputes over copyright infringement. To address these challenges, this paper introduces a novel approach that leverages the learning capacity of GenAI models for copyright legal analysis, demonstrated with GPT2 and Stable Diffusion models. Copyright law distinguishes between original expressions and generic ones (Sc\`enes \`a faire), protecting the former and permitting reproduction of the latter. However, this distinction has historically been challenging to make consistently, leading to over-protection of copyrighted works. GenAI offers an unprecedented opportunity to enhance this legal analysis by revealing shared patterns in preexisting works. We propose a data-driven approach to identify the genericity of works created by GenAI, employing "data-driven bias" to assess the genericity of expressive compositions. This approach aids in copyright scope determination by utilizing the capabilities of GenAI to identify and prioritize expressive elements and rank them according to their frequency in the model's dataset. The potential implications of measuring expressive genericity for copyright law are profound. Such scoring could assist courts in determining copyright scope during litigation, inform the registration practices of Copyright Offices, allowing registration of only highly original synthetic works, and help copyright owners signal the value of their works and facilitate fairer licensing deals. More generally, this approach offers valuable insights to policymakers grappling with adapting copyright law to the challenges posed by the era of GenAI.

Information Complexity of Stochastic Convex Optimization: Applications to Generalization and Memorization

In this work, we investigate the interplay between memorization and learning in the context of \emph{stochastic convex optimization} (SCO). We define memorization via the information a learning algorithm reveals about its training data points. We then quantify this information using the framework of conditional mutual information (CMI) proposed by Steinke and Zakynthinou (2020). Our main result is a precise characterization of the tradeoff between the accuracy of a learning algorithm and its CMI, answering an open question posed by Livni (2023). We show that, in the $L^2$ Lipschitz--bounded setting and under strong convexity, every learner with an excess error $\varepsilon$ has CMI bounded below by $\Omega(1/\varepsilon^2)$ and $\Omega(1/\varepsilon)$, respectively. We further demonstrate the essential role of memorization in learning problems in SCO by designing an adversary capable of accurately identifying a significant fraction of the training samples in specific SCO problems. Finally, we enumerate several implications of our results, such as a limitation of generalization bounds based on CMI and the incompressibility of samples in SCO problems.

The Sample Complexity Of ERMs In Stochastic Convex Optimization

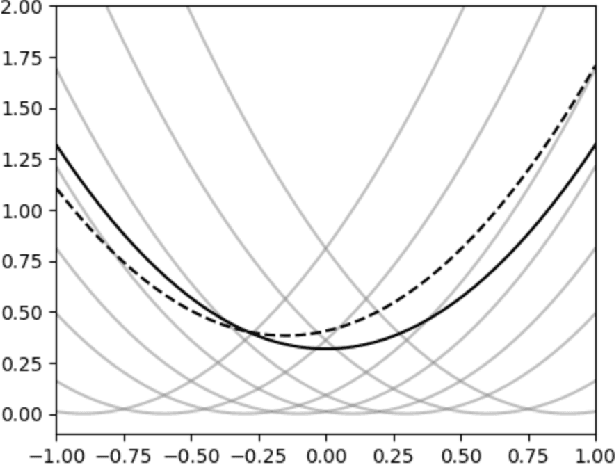
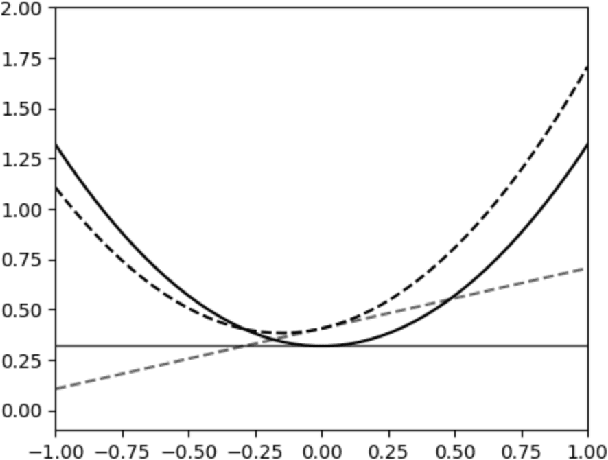
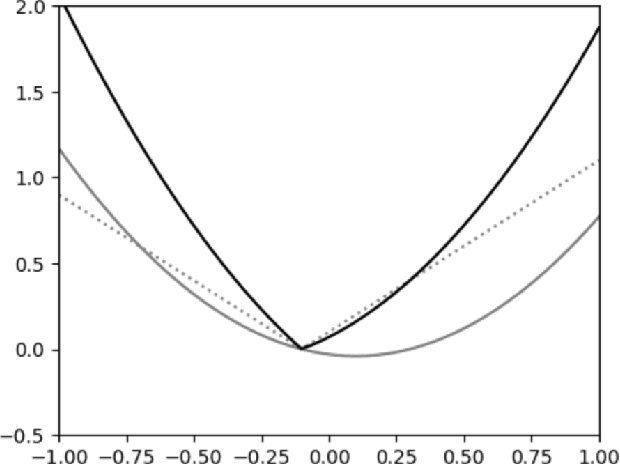
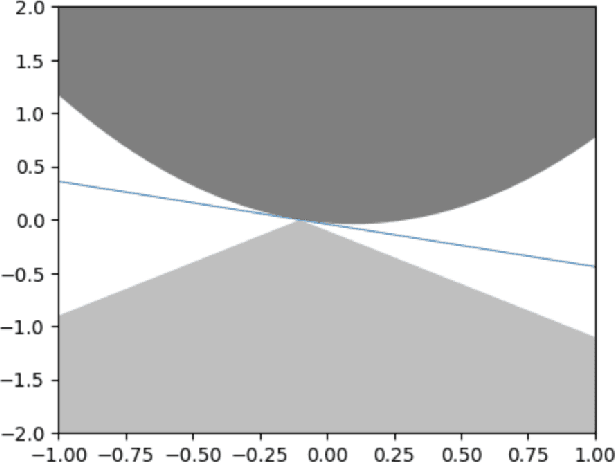
Stochastic convex optimization is one of the most well-studied models for learning in modern machine learning. Nevertheless, a central fundamental question in this setup remained unresolved: "How many data points must be observed so that any empirical risk minimizer (ERM) shows good performance on the true population?" This question was proposed by Feldman (2016), who proved that $\Omega(\frac{d}{\epsilon}+\frac{1}{\epsilon^2})$ data points are necessary (where $d$ is the dimension and $\epsilon>0$ is the accuracy parameter). Proving an $\omega(\frac{d}{\epsilon}+\frac{1}{\epsilon^2})$ lower bound was left as an open problem. In this work we show that in fact $\tilde{O}(\frac{d}{\epsilon}+\frac{1}{\epsilon^2})$ data points are also sufficient. This settles the question and yields a new separation between ERMs and uniform convergence. This sample complexity holds for the classical setup of learning bounded convex Lipschitz functions over the Euclidean unit ball. We further generalize the result and show that a similar upper bound holds for all symmetric convex bodies. The general bound is composed of two terms: (i) a term of the form $\tilde{O}(\frac{d}{\epsilon})$ with an inverse-linear dependence on the accuracy parameter, and (ii) a term that depends on the statistical complexity of the class of $\textit{linear}$ functions (captured by the Rademacher complexity). The proof builds a mechanism for controlling the behavior of stochastic convex optimization problems.

Can Copyright be Reduced to Privacy?

There is an increasing concern that generative AI models may produce outputs that are remarkably similar to the copyrighted input content on which they are trained. This worry has escalated as the quality and complexity of generative models have immensely improved, and the availability of large datasets containing copyrighted material has increased. Researchers are actively exploring strategies to mitigate the risk of producing infringing samples, and a recent line of work suggests to employ techniques such as differential privacy and other forms of algorithmic stability to safeguard copyrighted content. In this work, we examine the question whether algorithmic stability techniques such as differential privacy are suitable to ensure the responsible use of generative models without inadvertently violating copyright laws. We argue that there are fundamental differences between privacy and copyright that should not be overlooked. In particular we highlight that although algorithmic stability may be perceived as a practical tool to detect copying, it does not necessarily equate to copyright protection. Therefore, if it is adopted as standard for copyright infringement, it may undermine copyright law intended purposes.

Information Theoretic Lower Bounds for Information Theoretic Upper Bounds

We examine the relationship between the mutual information between the output model and the empirical sample and the generalization of the algorithm in the context of stochastic convex optimization. Despite increasing interest in information-theoretic generalization bounds, it is uncertain if these bounds can provide insight into the exceptional performance of various learning algorithms. Our study of stochastic convex optimization reveals that, for true risk minimization, dimension-dependent mutual information is necessary. This indicates that existing information-theoretic generalization bounds fall short in capturing the generalization capabilities of algorithms like SGD and regularized ERM, which have dimension-independent sample complexity.

Better Best of Both Worlds Bounds for Bandits with Switching Costs

We study best-of-both-worlds algorithms for bandits with switching cost, recently addressed by Rouyer, Seldin and Cesa-Bianchi, 2021. We introduce a surprisingly simple and effective algorithm that simultaneously achieves minimax optimal regret bound of $\mathcal{O}(T^{2/3})$ in the oblivious adversarial setting and a bound of $\mathcal{O}(\min\{\log (T)/\Delta^2,T^{2/3}\})$ in the stochastically-constrained regime, both with (unit) switching costs, where $\Delta$ is the gap between the arms. In the stochastically constrained case, our bound improves over previous results due to Rouyer et al., that achieved regret of $\mathcal{O}(T^{1/3}/\Delta)$. We accompany our results with a lower bound showing that, in general, $\tilde{\Omega}(\min\{1/\Delta^2,T^{2/3}\})$ regret is unavoidable in the stochastically-constrained case for algorithms with $\mathcal{O}(T^{2/3})$ worst-case regret.

Making Progress Based on False Discoveries

We consider the question of adaptive data analysis within the framework of convex optimization. We ask how many samples are needed in order to compute $\epsilon$-accurate estimates of $O(1/\epsilon^2)$ gradients queried by gradient descent, and we provide two intermediate answers to this question. First, we show that for a general analyst (not necessarily gradient descent) $\Omega(1/\epsilon^3)$ samples are required. This rules out the possibility of a foolproof mechanism. Our construction builds upon a new lower bound (that may be of interest of its own right) for an analyst that may ask several non adaptive questions in a batch of fixed and known $T$ rounds of adaptivity and requires a fraction of true discoveries. We show that for such an analyst $\Omega (\sqrt{T}/\epsilon^2)$ samples are necessary. Second, we show that, under certain assumptions on the oracle, in an interaction with gradient descent $\tilde \Omega(1/\epsilon^{2.5})$ samples are necessary. Our assumptions are that the oracle has only \emph{first order access} and is \emph{post-hoc generalizing}. First order access means that it can only compute the gradients of the sampled function at points queried by the algorithm. Our assumption of \emph{post-hoc generalization} follows from existing lower bounds for statistical queries. More generally then, we provide a generic reduction from the standard setting of statistical queries to the problem of estimating gradients queried by gradient descent. These results are in contrast with classical bounds that show that with $O(1/\epsilon^2)$ samples one can optimize the population risk to accuracy of $O(\epsilon)$ but, as it turns out, with spurious gradients.