Optimal Rates in Continual Linear Regression via Increasing Regularization

We study realizable continual linear regression under random task orderings, a common setting for developing continual learning theory. In this setup, the worst-case expected loss after $k$ learning iterations admits a lower bound of $\Omega(1/k)$. However, prior work using an unregularized scheme has only established an upper bound of $O(1/k^{1/4})$, leaving a significant gap. Our paper proves that this gap can be narrowed, or even closed, using two frequently used regularization schemes: (1) explicit isotropic $\ell_2$ regularization, and (2) implicit regularization via finite step budgets. We show that these approaches, which are used in practice to mitigate forgetting, reduce to stochastic gradient descent (SGD) on carefully defined surrogate losses. Through this lens, we identify a fixed regularization strength that yields a near-optimal rate of $O(\log k / k)$. Moreover, formalizing and analyzing a generalized variant of SGD for time-varying functions, we derive an increasing regularization strength schedule that provably achieves an optimal rate of $O(1/k)$. This suggests that schedules that increase the regularization coefficient or decrease the number of steps per task are beneficial, at least in the worst case.

Multiclass Loss Geometry Matters for Generalization of Gradient Descent in Separable Classification

We study the generalization performance of unregularized gradient methods for separable linear classification. While previous work mostly deal with the binary case, we focus on the multiclass setting with $k$ classes and establish novel population risk bounds for Gradient Descent for loss functions that decay to zero. In this setting, we show risk bounds that reveal that convergence rates are crucially influenced by the geometry of the loss template, as formalized by Wang and Scott (2024), rather than of the loss function itself. Particularly, we establish risk upper bounds that holds for any decay rate of the loss whose template is smooth with respect to the $p$-norm. In the case of exponentially decaying losses, our results indicates a contrast between the $p=\infty$ case, where the risk exhibits a logarithmic dependence on $k$, and $p=2$ where the risk scales linearly with $k$. To establish this separation formally, we also prove a lower bound in the latter scenario, demonstrating that the polynomial dependence on $k$ is unavoidable. Central to our analysis is a novel bound on the Rademacher complexity of low-noise vector-valued linear predictors with a loss template smooth w.r.t.~general $p$-norms.

Rapid Overfitting of Multi-Pass Stochastic Gradient Descent in Stochastic Convex Optimization

We study the out-of-sample performance of multi-pass stochastic gradient descent (SGD) in the fundamental stochastic convex optimization (SCO) model. While one-pass SGD is known to achieve an optimal $\Theta(1/\sqrt{n})$ excess population loss given a sample of size $n$, much less is understood about the multi-pass version of the algorithm which is widely used in practice. Somewhat surprisingly, we show that in the general non-smooth case of SCO, just a few epochs of SGD can already hurt its out-of-sample performance significantly and lead to overfitting. In particular, using a step size $\eta = \Theta(1/\sqrt{n})$, which gives the optimal rate after one pass, can lead to population loss as large as $\Omega(1)$ after just one additional pass. More generally, we show that the population loss from the second pass onward is of the order $\Theta(1/(\eta T) + \eta \sqrt{T})$, where $T$ is the total number of steps. These results reveal a certain phase-transition in the out-of-sample behavior of SGD after the first epoch, as well as a sharp separation between the rates of overfitting in the smooth and non-smooth cases of SCO. Additionally, we extend our results to with-replacement SGD, proving that the same asymptotic bounds hold after $O(n \log n)$ steps. Finally, we also prove a lower bound of $\Omega(\eta \sqrt{n})$ on the generalization gap of one-pass SGD in dimension $d = \smash{\widetilde O}(n)$, improving on recent results of Koren et al.(2022) and Schliserman et al.(2024).

Nearly Optimal Sample Complexity for Learning with Label Proportions

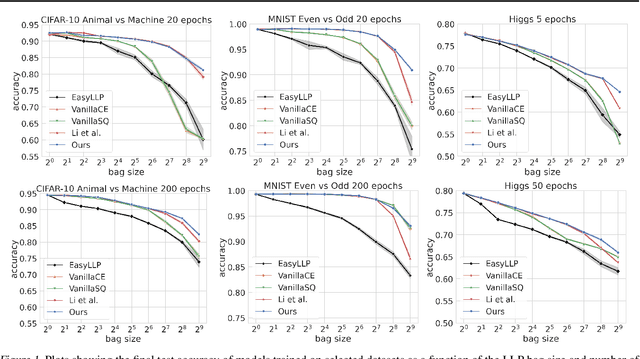
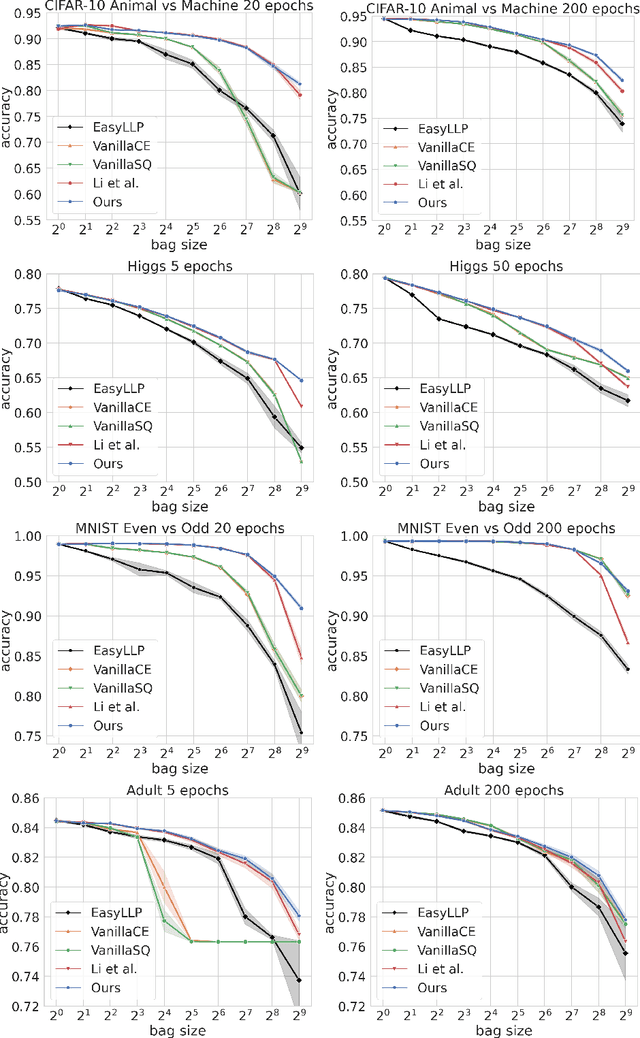
We investigate Learning from Label Proportions (LLP), a partial information setting where examples in a training set are grouped into bags, and only aggregate label values in each bag are available. Despite the partial observability, the goal is still to achieve small regret at the level of individual examples. We give results on the sample complexity of LLP under square loss, showing that our sample complexity is essentially optimal. From an algorithmic viewpoint, we rely on carefully designed variants of Empirical Risk Minimization, and Stochastic Gradient Descent algorithms, combined with ad hoc variance reduction techniques. On one hand, our theoretical results improve in important ways on the existing literature on LLP, specifically in the way the sample complexity depends on the bag size. On the other hand, we validate our algorithmic solutions on several datasets, demonstrating improved empirical performance (better accuracy for less samples) against recent baselines.

Better Rates for Random Task Orderings in Continual Linear Models

We study the common continual learning setup where an overparameterized model is sequentially fitted to a set of jointly realizable tasks. We analyze the forgetting, i.e., loss on previously seen tasks, after $k$ iterations. For linear models, we prove that fitting a task is equivalent to a single stochastic gradient descent (SGD) step on a modified objective. We develop novel last-iterate SGD upper bounds in the realizable least squares setup, and apply them to derive new results for continual learning. Focusing on random orderings over $T$ tasks, we establish universal forgetting rates, whereas existing rates depend on the problem dimensionality or complexity. Specifically, in continual regression with replacement, we improve the best existing rate from $O((d-r)/k)$ to $O(\min(k^{-1/4}, \sqrt{d-r}/k, \sqrt{Tr}/k))$, where $d$ is the dimensionality and $r$ the average task rank. Furthermore, we establish the first rates for random task orderings without replacement. The obtained rate of $O(\min(T^{-1/4}, (d-r)/T))$ proves for the first time that randomization alone, with no task repetition, can prevent catastrophic forgetting in sufficiently long task sequences. Finally, we prove a similar $O(k^{-1/4})$ universal rate for the forgetting in continual linear classification on separable data. Our universal rates apply for broader projection methods, such as block Kaczmarz and POCS, illuminating their loss convergence under i.i.d and one-pass orderings.

Benefits of Learning Rate Annealing for Tuning-Robustness in Stochastic Optimization

The learning rate in stochastic gradient methods is a critical hyperparameter that is notoriously costly to tune via standard grid search, especially for training modern large-scale models with billions of parameters. We identify a theoretical advantage of learning rate annealing schemes that decay the learning rate to zero at a polynomial rate, such as the widely-used cosine schedule, by demonstrating their increased robustness to initial parameter misspecification due to a coarse grid search. We present an analysis in a stochastic convex optimization setup demonstrating that the convergence rate of stochastic gradient descent with annealed schedules depends sublinearly on the multiplicative misspecification factor $\rho$ (i.e., the grid resolution), achieving a rate of $O(\rho^{1/(2p+1)}/\sqrt{T})$ where $p$ is the degree of polynomial decay and $T$ is the number of steps, in contrast to the $O(\rho/\sqrt{T})$ rate that arises with fixed stepsizes and exhibits a linear dependence on $\rho$. Experiments confirm the increased robustness compared to tuning with a fixed stepsize, that has significant implications for the computational overhead of hyperparameter search in practical training scenarios.

Bandit Multiclass List Classification

We study the problem of multiclass list classification with (semi-)bandit feedback, where input examples are mapped into subsets of size $m$ of a collection of $K$ possible labels, and the feedback consists of the predicted labels which lie in the set of true labels of the given example. Our main result is for the $(\varepsilon,\delta)$-PAC variant of the problem for which we design an algorithm that returns an $\varepsilon$-optimal hypothesis with high probability using a sample complexity of $O \big( (\mathrm{poly}(K/m) + sm / \varepsilon^2) \log (|H|/\delta) \big)$ where $H$ is the underlying (finite) hypothesis class and $s$ is an upper bound on the number of true labels for a given example. This bound improves upon known bounds for combinatorial semi-bandits whenever $s \ll K$. Moreover, in the regime where $s = O(1)$ the leading terms in our bound match the corresponding full-information rates, implying that bandit feedback essentially comes at no cost. Our PAC learning algorithm is also computationally efficient given access to an ERM oracle for $H$. Additionally, we consider the regret minimization setting where data can be generated adversarially, and establish a regret bound of $\widetilde O(|H| + \sqrt{smT \log |H|})$. Our results generalize and extend those of Erez et al. (2024) who consider the simpler single-label setting corresponding to $s=m=1$, and in fact hold for the more general contextual combinatorial semi-bandit problem with $s$-sparse rewards.

Complexity of Vector-valued Prediction: From Linear Models to Stochastic Convex Optimization

We study the problem of learning vector-valued linear predictors: these are prediction rules parameterized by a matrix that maps an $m$-dimensional feature vector to a $k$-dimensional target. We focus on the fundamental case with a convex and Lipschitz loss function, and show several new theoretical results that shed light on the complexity of this problem and its connection to related learning models. First, we give a tight characterization of the sample complexity of Empirical Risk Minimization (ERM) in this setting, establishing that $\smash{\widetilde{\Omega}}(k/\epsilon^2)$ examples are necessary for ERM to reach $\epsilon$ excess (population) risk; this provides for an exponential improvement over recent results by Magen and Shamir (2023) in terms of the dependence on the target dimension $k$, and matches a classical upper bound due to Maurer (2016). Second, we present a black-box conversion from general $d$-dimensional Stochastic Convex Optimization (SCO) to vector-valued linear prediction, showing that any SCO problem can be embedded as a prediction problem with $k=\Theta(d)$ outputs. These results portray the setting of vector-valued linear prediction as bridging between two extensively studied yet disparate learning models: linear models (corresponds to $k=1$) and general $d$-dimensional SCO (with $k=\Theta(d)$).

Faster Stochastic Optimization with Arbitrary Delays via Asynchronous Mini-Batching

We consider the problem of asynchronous stochastic optimization, where an optimization algorithm makes updates based on stale stochastic gradients of the objective that are subject to an arbitrary (possibly adversarial) sequence of delays. We present a procedure which, for any given $q \in (0,1]$, transforms any standard stochastic first-order method to an asynchronous method with convergence guarantee depending on the $q$-quantile delay of the sequence. This approach leads to convergence rates of the form $O(\tau_q/qT+\sigma/\sqrt{qT})$ for non-convex and $O(\tau_q^2/(q T)^2+\sigma/\sqrt{qT})$ for convex smooth problems, where $\tau_q$ is the $q$-quantile delay, generalizing and improving on existing results that depend on the average delay. We further show a method that automatically adapts to all quantiles simultaneously, without any prior knowledge of the delays, achieving convergence rates of the form $O(\inf_{q} \tau_q/qT+\sigma/\sqrt{qT})$ for non-convex and $O(\inf_{q} \tau_q^2/(q T)^2+\sigma/\sqrt{qT})$ for convex smooth problems. Our technique is based on asynchronous mini-batching with a careful batch-size selection and filtering of stale gradients.

Fast Rates for Bandit PAC Multiclass Classification

We study multiclass PAC learning with bandit feedback, where inputs are classified into one of $K$ possible labels and feedback is limited to whether or not the predicted labels are correct. Our main contribution is in designing a novel learning algorithm for the agnostic $(\varepsilon,\delta)$-PAC version of the problem, with sample complexity of $O\big( (\operatorname{poly}(K) + 1 / \varepsilon^2) \log (|H| / \delta) \big)$ for any finite hypothesis class $H$. In terms of the leading dependence on $\varepsilon$, this improves upon existing bounds for the problem, that are of the form $O(K/\varepsilon^2)$. We also provide an extension of this result to general classes and establish similar sample complexity bounds in which $\log |H|$ is replaced by the Natarajan dimension. This matches the optimal rate in the full-information version of the problem and resolves an open question studied by Daniely, Sabato, Ben-David, and Shalev-Shwartz (2011) who demonstrated that the multiplicative price of bandit feedback in realizable PAC learning is $\Theta(K)$. We complement this by revealing a stark contrast with the agnostic case, where the price of bandit feedback is only $O(1)$ as $\varepsilon \to 0$. Our algorithm utilizes a stochastic optimization technique to minimize a log-barrier potential based on Frank-Wolfe updates for computing a low-variance exploration distribution over the hypotheses, and is made computationally efficient provided access to an ERM oracle over $H$.