Tensor-Parallelism with Partially Synchronized Activations

Training and inference of Large Language Models (LLMs) with tensor-parallelism requires substantial communication to synchronize activations. Our findings suggest that with a few minor adjustments to current practices, LLMs can be trained without fully synchronizing activations, reducing bandwidth demands. We name this "Communication-Aware Architecture for Tensor-parallelism" (CAAT-Net). We train 1B and 7B parameter CAAT-Net models, with a 50% reduction in tensor-parallel communication and no significant drop in pretraining accuracy. Furthermore, we demonstrate how CAAT-Net accelerates both training and inference workloads.

When Diffusion Models Memorize: Inductive Biases in Probability Flow of Minimum-Norm Shallow Neural Nets

While diffusion models generate high-quality images via probability flow, the theoretical understanding of this process remains incomplete. A key question is when probability flow converges to training samples or more general points on the data manifold. We analyze this by studying the probability flow of shallow ReLU neural network denoisers trained with minimal $\ell^2$ norm. For intuition, we introduce a simpler score flow and show that for orthogonal datasets, both flows follow similar trajectories, converging to a training point or a sum of training points. However, early stopping by the diffusion time scheduler allows probability flow to reach more general manifold points. This reflects the tendency of diffusion models to both memorize training samples and generate novel points that combine aspects of multiple samples, motivating our study of such behavior in simplified settings. We extend these results to obtuse simplex data and, through simulations in the orthogonal case, confirm that probability flow converges to a training point, a sum of training points, or a manifold point. Moreover, memorization decreases when the number of training samples grows, as fewer samples accumulate near training points.

Optimal Rates in Continual Linear Regression via Increasing Regularization

We study realizable continual linear regression under random task orderings, a common setting for developing continual learning theory. In this setup, the worst-case expected loss after $k$ learning iterations admits a lower bound of $\Omega(1/k)$. However, prior work using an unregularized scheme has only established an upper bound of $O(1/k^{1/4})$, leaving a significant gap. Our paper proves that this gap can be narrowed, or even closed, using two frequently used regularization schemes: (1) explicit isotropic $\ell_2$ regularization, and (2) implicit regularization via finite step budgets. We show that these approaches, which are used in practice to mitigate forgetting, reduce to stochastic gradient descent (SGD) on carefully defined surrogate losses. Through this lens, we identify a fixed regularization strength that yields a near-optimal rate of $O(\log k / k)$. Moreover, formalizing and analyzing a generalized variant of SGD for time-varying functions, we derive an increasing regularization strength schedule that provably achieves an optimal rate of $O(1/k)$. This suggests that schedules that increase the regularization coefficient or decrease the number of steps per task are beneficial, at least in the worst case.

FP4 All the Way: Fully Quantized Training of LLMs

We demonstrate, for the first time, fully quantized training (FQT) of large language models (LLMs) using predominantly 4-bit floating-point (FP4) precision for weights, activations, and gradients on datasets up to 200 billion tokens. We extensively investigate key design choices for FP4, including block sizes, scaling formats, and rounding methods. Our analysis shows that the NVFP4 format, where each block of 16 FP4 values (E2M1) shares a scale represented in E4M3, provides optimal results. We use stochastic rounding for backward and update passes and round-to-nearest for the forward pass to enhance stability. Additionally, we identify a theoretical and empirical threshold for effective quantized training: when the gradient norm falls below approximately $\sqrt{3}$ times the quantization noise, quantized training becomes less effective. Leveraging these insights, we successfully train a 7-billion-parameter model on 256 Intel Gaudi2 accelerators. The resulting FP4-trained model achieves downstream task performance comparable to a standard BF16 baseline, confirming that FP4 training is a practical and highly efficient approach for large-scale LLM training. A reference implementation is supplied in https://github.com/Anonymous1252022/fp4-all-the-way .

Temperature is All You Need for Generalization in Langevin Dynamics and other Markov Processes

We analyze the generalization gap (gap between the training and test errors) when training a potentially over-parametrized model using a Markovian stochastic training algorithm, initialized from some distribution $\theta_0 \sim p_0$. We focus on Langevin dynamics with a positive temperature $\beta^{-1}$, i.e. gradient descent on a training loss $L$ with infinitesimal step size, perturbed with $\beta^{-1}$-variances Gaussian noise, and lightly regularized or bounded. There, we bound the generalization gap, at any time during training, by $\sqrt{(\beta\mathbb{E} L (\theta_0) + \log(1/\delta))/N}$ with probability $1-\delta$ over the dataset, where $N$ is the sample size, and $\mathbb{E} L (\theta_0) =O(1)$ with standard initialization scaling. In contrast to previous guarantees, we have no dependence on either training time or reliance on mixing, nor a dependence on dimensionality, gradient norms, or any other properties of the loss or model. This guarantee follows from a general analysis of any Markov process-based training that has a Gibbs-style stationary distribution. The proof is surprisingly simple, once we observe that the marginal distribution divergence from initialization remains bounded, as implied by a generalized second law of thermodynamics.

PLUMAGE: Probabilistic Low rank Unbiased Min Variance Gradient Estimator for Efficient Large Model Training

Accelerator memory and networking constraints have emerged as dominant bottlenecks when training large language models LLMs with billions of parameters. Existing low rank gradient estimators such as GaLoRE and FLORA compress gradients and optimizer tensors by projecting weight gradients onto a rank r subspace, enabling LLM training on consumer hardware. Yet, these methods are either biased or subject to high estimator variance. Moreover, the optimizer state based on the first and second moments estimates expressed in the previous subspace becomes misaligned whenever the projection is updated, leading to instabilities during training. We propose PLUMAGE: Probabilistic Low rank Unbiased Minimum vAriance Gradient Estimator. PLUMAGE is a drop in replacement for existing low rank gradient estimators. It does not introduce new hyperparameters beyond the chosen rank r and the update interval. In addition, we resolve optimizer state misalignment issues to prevent spurious weight updates and enhance training stability. We empirically demonstrate that PLUMAGE shrinks the full rank optimization's gap over the pre training evaluation loss by 33% on average across models and the average training loss across the GLUE benchmark by 28% within a similar computational and memory footprint as GaloRE.

Better Rates for Random Task Orderings in Continual Linear Models

We study the common continual learning setup where an overparameterized model is sequentially fitted to a set of jointly realizable tasks. We analyze the forgetting, i.e., loss on previously seen tasks, after $k$ iterations. For linear models, we prove that fitting a task is equivalent to a single stochastic gradient descent (SGD) step on a modified objective. We develop novel last-iterate SGD upper bounds in the realizable least squares setup, and apply them to derive new results for continual learning. Focusing on random orderings over $T$ tasks, we establish universal forgetting rates, whereas existing rates depend on the problem dimensionality or complexity. Specifically, in continual regression with replacement, we improve the best existing rate from $O((d-r)/k)$ to $O(\min(k^{-1/4}, \sqrt{d-r}/k, \sqrt{Tr}/k))$, where $d$ is the dimensionality and $r$ the average task rank. Furthermore, we establish the first rates for random task orderings without replacement. The obtained rate of $O(\min(T^{-1/4}, (d-r)/T))$ proves for the first time that randomization alone, with no task repetition, can prevent catastrophic forgetting in sufficiently long task sequences. Finally, we prove a similar $O(k^{-1/4})$ universal rate for the forgetting in continual linear classification on separable data. Our universal rates apply for broader projection methods, such as block Kaczmarz and POCS, illuminating their loss convergence under i.i.d and one-pass orderings.

Provable Tempered Overfitting of Minimal Nets and Typical Nets

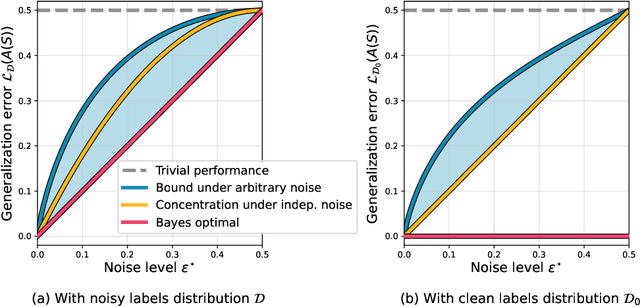
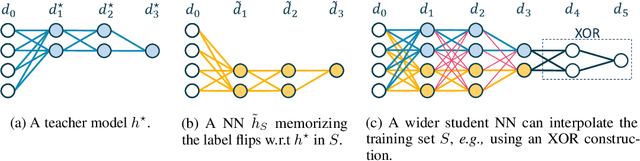
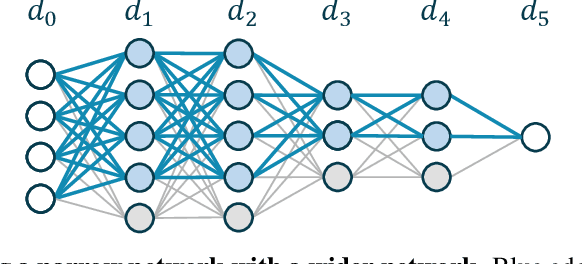
We study the overfitting behavior of fully connected deep Neural Networks (NNs) with binary weights fitted to perfectly classify a noisy training set. We consider interpolation using both the smallest NN (having the minimal number of weights) and a random interpolating NN. For both learning rules, we prove overfitting is tempered. Our analysis rests on a new bound on the size of a threshold circuit consistent with a partial function. To the best of our knowledge, ours are the first theoretical results on benign or tempered overfitting that: (1) apply to deep NNs, and (2) do not require a very high or very low input dimension.

Foldable SuperNets: Scalable Merging of Transformers with Different Initializations and Tasks

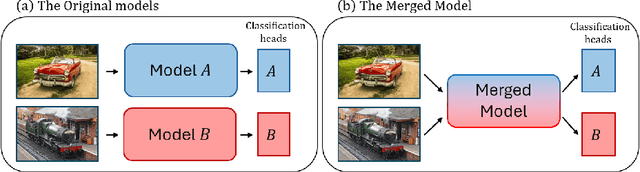
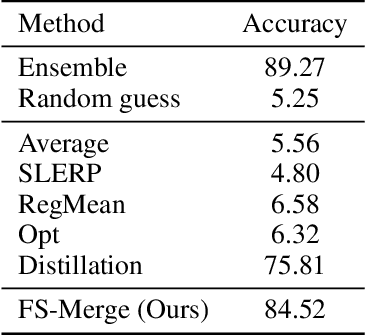
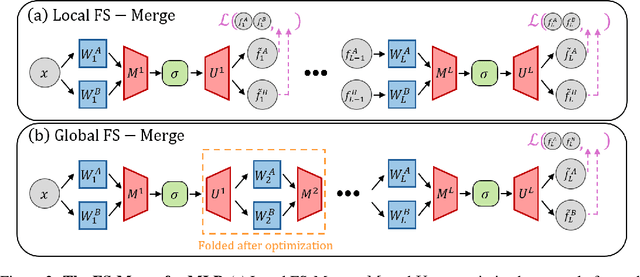
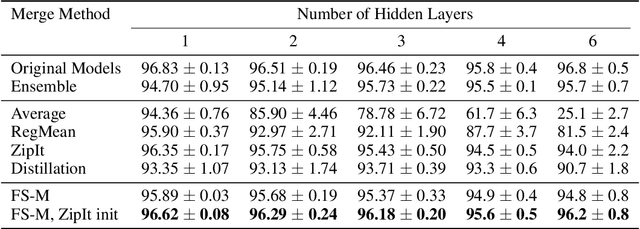
Many recent methods aim to merge neural networks (NNs) with identical architectures trained on different tasks to obtain a single multi-task model. Most existing works tackle the simpler setup of merging NNs initialized from a common pre-trained network, where simple heuristics like weight averaging work well. This work targets a more challenging goal: merging large transformers trained on different tasks from distinct initializations. First, we demonstrate that traditional merging methods fail catastrophically in this setup. To overcome this challenge, we propose Foldable SuperNet Merge (FS-Merge), a method that optimizes a SuperNet to fuse the original models using a feature reconstruction loss. FS-Merge is simple, data-efficient, and capable of merging models of varying widths. We test FS-Merge against existing methods, including knowledge distillation, on MLPs and transformers across various settings, sizes, tasks, and modalities. FS-Merge consistently outperforms them, achieving SOTA results, particularly in limited data scenarios.

Stable Minima Cannot Overfit in Univariate ReLU Networks: Generalization by Large Step Sizes

We study the generalization of two-layer ReLU neural networks in a univariate nonparametric regression problem with noisy labels. This is a problem where kernels (\emph{e.g.} NTK) are provably sub-optimal and benign overfitting does not happen, thus disqualifying existing theory for interpolating (0-loss, global optimal) solutions. We present a new theory of generalization for local minima that gradient descent with a constant learning rate can \emph{stably} converge to. We show that gradient descent with a fixed learning rate $\eta$ can only find local minima that represent smooth functions with a certain weighted \emph{first order total variation} bounded by $1/\eta - 1/2 + \widetilde{O}(\sigma + \sqrt{\mathrm{MSE}})$ where $\sigma$ is the label noise level, $\mathrm{MSE}$ is short for mean squared error against the ground truth, and $\widetilde{O}(\cdot)$ hides a logarithmic factor. Under mild assumptions, we also prove a nearly-optimal MSE bound of $\widetilde{O}(n^{-4/5})$ within the strict interior of the support of the $n$ data points. Our theoretical results are validated by extensive simulation that demonstrates large learning rate training induces sparse linear spline fits. To the best of our knowledge, we are the first to obtain generalization bound via minima stability in the non-interpolation case and the first to show ReLU NNs without regularization can achieve near-optimal rates in nonparametric regression.