Provable Tempered Overfitting of Minimal Nets and Typical Nets
Paper and Code
Oct 24, 2024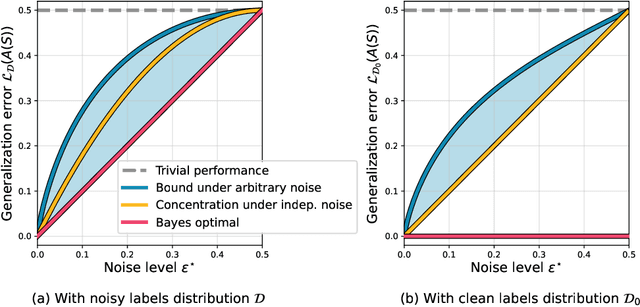
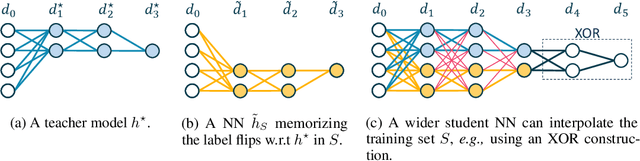
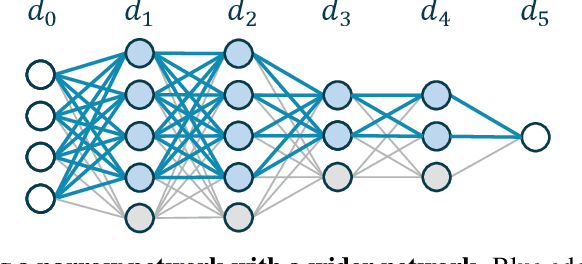
We study the overfitting behavior of fully connected deep Neural Networks (NNs) with binary weights fitted to perfectly classify a noisy training set. We consider interpolation using both the smallest NN (having the minimal number of weights) and a random interpolating NN. For both learning rules, we prove overfitting is tempered. Our analysis rests on a new bound on the size of a threshold circuit consistent with a partial function. To the best of our knowledge, ours are the first theoretical results on benign or tempered overfitting that: (1) apply to deep NNs, and (2) do not require a very high or very low input dimension.
* 60 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge