Temperature is All You Need for Generalization in Langevin Dynamics and other Markov Processes

We analyze the generalization gap (gap between the training and test errors) when training a potentially over-parametrized model using a Markovian stochastic training algorithm, initialized from some distribution $\theta_0 \sim p_0$. We focus on Langevin dynamics with a positive temperature $\beta^{-1}$, i.e. gradient descent on a training loss $L$ with infinitesimal step size, perturbed with $\beta^{-1}$-variances Gaussian noise, and lightly regularized or bounded. There, we bound the generalization gap, at any time during training, by $\sqrt{(\beta\mathbb{E} L (\theta_0) + \log(1/\delta))/N}$ with probability $1-\delta$ over the dataset, where $N$ is the sample size, and $\mathbb{E} L (\theta_0) =O(1)$ with standard initialization scaling. In contrast to previous guarantees, we have no dependence on either training time or reliance on mixing, nor a dependence on dimensionality, gradient norms, or any other properties of the loss or model. This guarantee follows from a general analysis of any Markov process-based training that has a Gibbs-style stationary distribution. The proof is surprisingly simple, once we observe that the marginal distribution divergence from initialization remains bounded, as implied by a generalized second law of thermodynamics.

A Theory of Learning with Autoregressive Chain of Thought

For a given base class of sequence-to-next-token generators, we consider learning prompt-to-answer mappings obtained by iterating a fixed, time-invariant generator for multiple steps, thus generating a chain-of-thought, and then taking the final token as the answer. We formalize the learning problems both when the chain-of-thought is observed and when training only on prompt-answer pairs, with the chain-of-thought latent. We analyze the sample and computational complexity both in terms of general properties of the base class (e.g. its VC dimension) and for specific base classes such as linear thresholds. We present a simple base class that allows for universal representability and computationally tractable chain-of-thought learning. Central to our development is that time invariance allows for sample complexity that is independent of the length of the chain-of-thought. Attention arises naturally in our construction.

Flavors of Margin: Implicit Bias of Steepest Descent in Homogeneous Neural Networks

We study the implicit bias of the general family of steepest descent algorithms, which includes gradient descent, sign descent and coordinate descent, in deep homogeneous neural networks. We prove that an algorithm-dependent geometric margin starts increasing once the networks reach perfect training accuracy and characterize the late-stage bias of the algorithms. In particular, we define a generalized notion of stationarity for optimization problems and show that the algorithms progressively reduce a (generalized) Bregman divergence, which quantifies proximity to such stationary points of a margin-maximization problem. We then experimentally zoom into the trajectories of neural networks optimized with various steepest descent algorithms, highlighting connections to the implicit bias of Adam.

Provable Tempered Overfitting of Minimal Nets and Typical Nets

We study the overfitting behavior of fully connected deep Neural Networks (NNs) with binary weights fitted to perfectly classify a noisy training set. We consider interpolation using both the smallest NN (having the minimal number of weights) and a random interpolating NN. For both learning rules, we prove overfitting is tempered. Our analysis rests on a new bound on the size of a threshold circuit consistent with a partial function. To the best of our knowledge, ours are the first theoretical results on benign or tempered overfitting that: (1) apply to deep NNs, and (2) do not require a very high or very low input dimension.

Benign Overfitting in Single-Head Attention

The phenomenon of benign overfitting, where a trained neural network perfectly fits noisy training data but still achieves near-optimal test performance, has been extensively studied in recent years for linear models and fully-connected/convolutional networks. In this work, we study benign overfitting in a single-head softmax attention model, which is the fundamental building block of Transformers. We prove that under appropriate conditions, the model exhibits benign overfitting in a classification setting already after two steps of gradient descent. Moreover, we show conditions where a minimum-norm/maximum-margin interpolator exhibits benign overfitting. We study how the overfitting behavior depends on the signal-to-noise ratio (SNR) of the data distribution, namely, the ratio between norms of signal and noise tokens, and prove that a sufficiently large SNR is both necessary and sufficient for benign overfitting.

Provable Privacy Attacks on Trained Shallow Neural Networks

We study what provable privacy attacks can be shown on trained, 2-layer ReLU neural networks. We explore two types of attacks; data reconstruction attacks, and membership inference attacks. We prove that theoretical results on the implicit bias of 2-layer neural networks can be used to provably reconstruct a set of which at least a constant fraction are training points in a univariate setting, and can also be used to identify with high probability whether a given point was used in the training set in a high dimensional setting. To the best of our knowledge, our work is the first to show provable vulnerabilities in this setting.

Trained Transformer Classifiers Generalize and Exhibit Benign Overfitting In-Context

Transformers have the capacity to act as supervised learning algorithms: by properly encoding a set of labeled training ("in-context") examples and an unlabeled test example into an input sequence of vectors of the same dimension, the forward pass of the transformer can produce predictions for that unlabeled test example. A line of recent work has shown that when linear transformers are pre-trained on random instances for linear regression tasks, these trained transformers make predictions using an algorithm similar to that of ordinary least squares. In this work, we investigate the behavior of linear transformers trained on random linear classification tasks. Via an analysis of the implicit regularization of gradient descent, we characterize how many pre-training tasks and in-context examples are needed for the trained transformer to generalize well at test-time. We further show that in some settings, these trained transformers can exhibit "benign overfitting in-context": when in-context examples are corrupted by label flipping noise, the transformer memorizes all of its in-context examples (including those with noisy labels) yet still generalizes near-optimally for clean test examples.

Overfitting Behaviour of Gaussian Kernel Ridgeless Regression: Varying Bandwidth or Dimensionality

We consider the overfitting behavior of minimum norm interpolating solutions of Gaussian kernel ridge regression (i.e. kernel ridgeless regression), when the bandwidth or input dimension varies with the sample size. For fixed dimensions, we show that even with varying or tuned bandwidth, the ridgeless solution is never consistent and, at least with large enough noise, always worse than the null predictor. For increasing dimension, we give a generic characterization of the overfitting behavior for any scaling of the dimension with sample size. We use this to provide the first example of benign overfitting using the Gaussian kernel with sub-polynomial scaling dimension. All our results are under the Gaussian universality ansatz and the (non-rigorous) risk predictions in terms of the kernel eigenstructure.

Approaching Deep Learning through the Spectral Dynamics of Weights

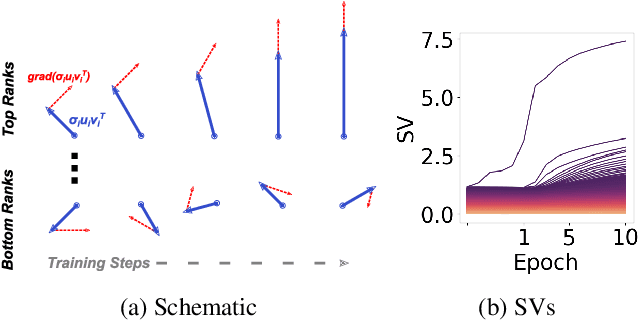
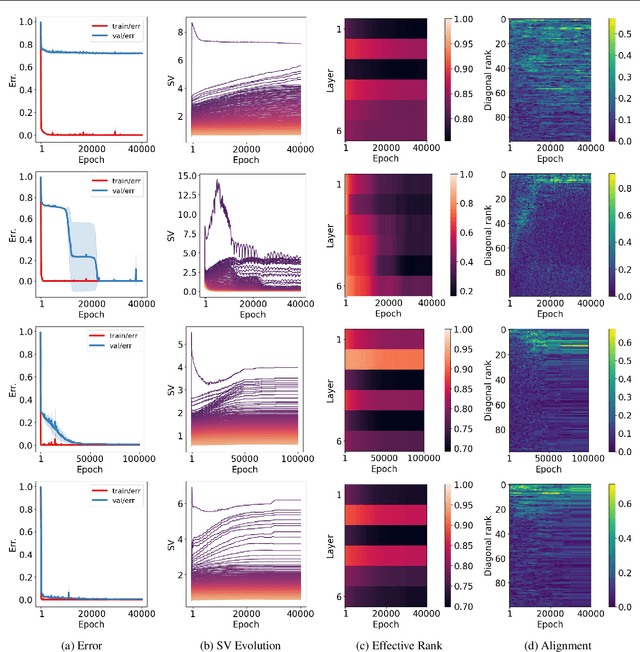
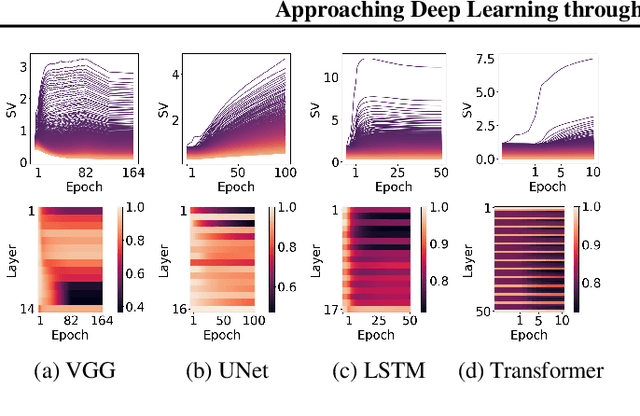
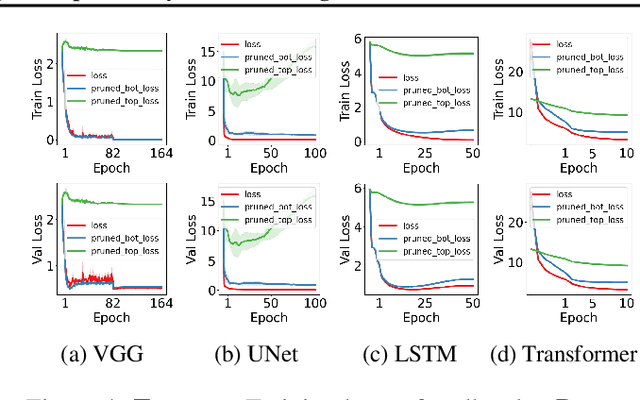
We propose an empirical approach centered on the spectral dynamics of weights -- the behavior of singular values and vectors during optimization -- to unify and clarify several phenomena in deep learning. We identify a consistent bias in optimization across various experiments, from small-scale ``grokking'' to large-scale tasks like image classification with ConvNets, image generation with UNets, speech recognition with LSTMs, and language modeling with Transformers. We also demonstrate that weight decay enhances this bias beyond its role as a norm regularizer, even in practical systems. Moreover, we show that these spectral dynamics distinguish memorizing networks from generalizing ones, offering a novel perspective on this longstanding conundrum. Additionally, we leverage spectral dynamics to explore the emergence of well-performing sparse subnetworks (lottery tickets) and the structure of the loss surface through linear mode connectivity. Our findings suggest that spectral dynamics provide a coherent framework to better understand the behavior of neural networks across diverse settings.

Reconstructing Training Data From Real World Models Trained with Transfer Learning

Current methods for reconstructing training data from trained classifiers are restricted to very small models, limited training set sizes, and low-resolution images. Such restrictions hinder their applicability to real-world scenarios. In this paper, we present a novel approach enabling data reconstruction in realistic settings for models trained on high-resolution images. Our method adapts the reconstruction scheme of arXiv:2206.07758 to real-world scenarios -- specifically, targeting models trained via transfer learning over image embeddings of large pre-trained models like DINO-ViT and CLIP. Our work employs data reconstruction in the embedding space rather than in the image space, showcasing its applicability beyond visual data. Moreover, we introduce a novel clustering-based method to identify good reconstructions from thousands of candidates. This significantly improves on previous works that relied on knowledge of the training set to identify good reconstructed images. Our findings shed light on a potential privacy risk for data leakage from models trained using transfer learning.