Likelihood-Based Reward Designs for General LLM Reasoning

Fine-tuning large language models (LLMs) on reasoning benchmarks via reinforcement learning requires a specific reward function, often binary, for each benchmark. This comes with two potential limitations: the need to design the reward, and the potentially sparse nature of binary rewards. Here, we systematically investigate rewards derived from the probability or log-probability of emitting the reference answer (or any other prompt continuation present in the data), which have the advantage of not relying on specific verifiers and being available at scale. Several recent works have advocated for the use of similar rewards (e.g., VeriFree, JEPO, RLPR, NOVER). We systematically compare variants of likelihood-based rewards with standard baselines, testing performance both on standard mathematical reasoning benchmarks, and on long-form answers where no external verifier is available. We find that using the log-probability of the reference answer as the reward for chain-of-thought (CoT) learning is the only option that performs well in all setups. This reward is also consistent with the next-token log-likelihood loss used during pretraining. In verifiable settings, log-probability rewards bring comparable or better success rates than reinforcing with standard binary rewards, and yield much better perplexity. In non-verifiable settings, they perform on par with SFT. On the other hand, methods based on probability, such as VeriFree, flatline on non-verifiable settings due to vanishing probabilities of getting the correct answer. Overall, this establishes log-probability rewards as a viable method for CoT fine-tuning, bridging the short, verifiable and long, non-verifiable answer settings.

Teaching Models to Teach Themselves: Reasoning at the Edge of Learnability

Can a model learn to escape its own learning plateau? Reinforcement learning methods for finetuning large reasoning models stall on datasets with low initial success rates, and thus little training signal. We investigate a fundamental question: Can a pretrained LLM leverage latent knowledge to generate an automated curriculum for problems it cannot solve? To explore this, we design SOAR: A self-improvement framework designed to surface these pedagogical signals through meta-RL. A teacher copy of the model proposes synthetic problems for a student copy, and is rewarded with its improvement on a small subset of hard problems. Critically, SOAR grounds the curriculum in measured student progress rather than intrinsic proxy rewards. Our study on the hardest subsets of mathematical benchmarks (0/128 success) reveals three core findings. First, we show that it is possible to realize bi-level meta-RL that unlocks learning under sparse, binary rewards by sharpening a latent capacity of pretrained models to generate useful stepping stones. Second, grounded rewards outperform intrinsic reward schemes used in prior LLM self-play, reliably avoiding the instability and diversity collapse modes they typically exhibit. Third, analyzing the generated questions reveals that structural quality and well-posedness are more critical for learning progress than solution correctness. Our results suggest that the ability to generate useful stepping stones does not require the preexisting ability to actually solve the hard problems, paving a principled path to escape reasoning plateaus without additional curated data.

Outcome-based Exploration for LLM Reasoning

Reinforcement learning (RL) has emerged as a powerful method for improving the reasoning abilities of large language models (LLMs). Outcome-based RL, which rewards policies solely for the correctness of the final answer, yields substantial accuracy gains but also induces a systematic loss in generation diversity. This collapse undermines real-world performance, where diversity is critical for test-time scaling. We analyze this phenomenon by viewing RL post-training as a sampling process and show that, strikingly, RL can reduce effective diversity even on the training set relative to the base model. Our study highlights two central findings: (i) a transfer of diversity degradation, where reduced diversity on solved problems propagates to unsolved ones, and (ii) the tractability of the outcome space, since reasoning tasks admit only a limited set of distinct answers. Motivated by these insights, we propose outcome-based exploration, which assigns exploration bonuses according to final outcomes. We introduce two complementary algorithms: historical exploration, which encourages rarely observed answers via UCB-style bonuses, and batch exploration, which penalizes within-batch repetition to promote test-time diversity. Experiments on standard competition math with Llama and Qwen models demonstrate that both methods improve accuracy while mitigating diversity collapse. On the theoretical side, we formalize the benefit of outcome-based exploration through a new model of outcome-based bandits. Together, these contributions chart a practical path toward RL methods that enhance reasoning without sacrificing the diversity essential for scalable deployment.

Tuning without Peeking: Provable Privacy and Generalization Bounds for LLM Post-Training

Gradient-based optimization is the workhorse of deep learning, offering efficient and scalable training via backpropagation. However, its reliance on large volumes of labeled data raises privacy and security concerns such as susceptibility to data poisoning attacks and the risk of overfitting. In contrast, black box optimization methods, which treat the model as an opaque function, relying solely on function evaluations to guide optimization, offer a promising alternative in scenarios where data access is restricted, adversarial risks are high, or overfitting is a concern. However, black box methods also pose significant challenges, including poor scalability to high-dimensional parameter spaces, as prevalent in large language models (LLMs), and high computational costs due to reliance on numerous model evaluations. This paper introduces BBoxER, an evolutionary black-box method for LLM post-training that induces an information bottleneck via implicit compression of the training data. Leveraging the tractability of information flow, we provide strong theoretical bounds on generalization, differential privacy, susceptibility to data poisoning attacks, and robustness to extraction attacks. BBoxER operates on top of pre-trained LLMs, offering a lightweight and modular enhancement suitable for deployment in restricted or privacy-sensitive environments, in addition to non-vacuous generalization guarantees. In experiments with LLMs, we demonstrate empirically that Retrofitting methods are able to learn, showing how a few iterations of BBoxER improve performance and generalize well on a benchmark of reasoning datasets. This positions BBoxER as an attractive add-on on top of gradient-based optimization.

PILAF: Optimal Human Preference Sampling for Reward Modeling

As large language models increasingly drive real-world applications, aligning them with human values becomes paramount. Reinforcement Learning from Human Feedback (RLHF) has emerged as a key technique, translating preference data into reward models when oracle human values remain inaccessible. In practice, RLHF mostly relies on approximate reward models, which may not consistently guide the policy toward maximizing the underlying human values. We propose Policy-Interpolated Learning for Aligned Feedback (PILAF), a novel response sampling strategy for preference labeling that explicitly aligns preference learning with maximizing the underlying oracle reward. PILAF is theoretically grounded, demonstrating optimality from both an optimization and a statistical perspective. The method is straightforward to implement and demonstrates strong performance in iterative and online RLHF settings where feedback curation is critical.

Flavors of Margin: Implicit Bias of Steepest Descent in Homogeneous Neural Networks

We study the implicit bias of the general family of steepest descent algorithms, which includes gradient descent, sign descent and coordinate descent, in deep homogeneous neural networks. We prove that an algorithm-dependent geometric margin starts increasing once the networks reach perfect training accuracy and characterize the late-stage bias of the algorithms. In particular, we define a generalized notion of stationarity for optimization problems and show that the algorithms progressively reduce a (generalized) Bregman divergence, which quantifies proximity to such stationary points of a margin-maximization problem. We then experimentally zoom into the trajectories of neural networks optimized with various steepest descent algorithms, highlighting connections to the implicit bias of Adam.

On the Geometry of Regularization in Adversarial Training: High-Dimensional Asymptotics and Generalization Bounds

Regularization, whether explicit in terms of a penalty in the loss or implicit in the choice of algorithm, is a cornerstone of modern machine learning. Indeed, controlling the complexity of the model class is particularly important when data is scarce, noisy or contaminated, as it translates a statistical belief on the underlying structure of the data. This work investigates the question of how to choose the regularization norm $\lVert \cdot \rVert$ in the context of high-dimensional adversarial training for binary classification. To this end, we first derive an exact asymptotic description of the robust, regularized empirical risk minimizer for various types of adversarial attacks and regularization norms (including non-$\ell_p$ norms). We complement this analysis with a uniform convergence analysis, deriving bounds on the Rademacher Complexity for this class of problems. Leveraging our theoretical results, we quantitatively characterize the relationship between perturbation size and the optimal choice of $\lVert \cdot \rVert$, confirming the intuition that, in the data scarce regime, the type of regularization becomes increasingly important for adversarial training as perturbations grow in size.

Emergent properties with repeated examples

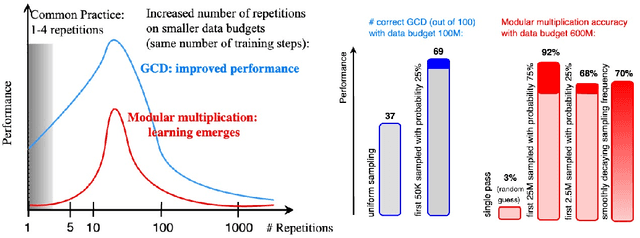
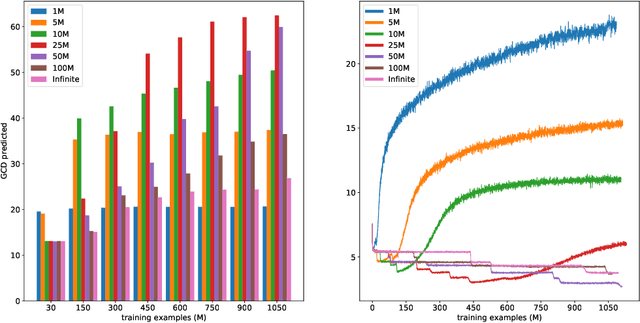
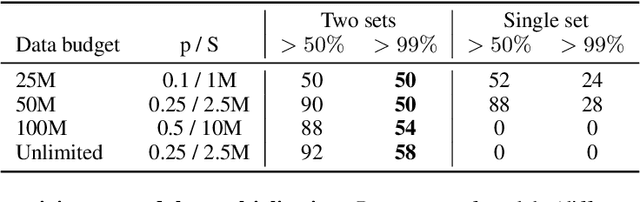
We study the performance of transformers as a function of the number of repetitions of training examples with algorithmically generated datasets. On three problems of mathematics: the greatest common divisor, modular multiplication, and matrix eigenvalues, we show that for a fixed number of training steps, models trained on smaller sets of repeated examples outperform models trained on larger sets of single-use examples. We also demonstrate that two-set training - repeated use of a small random subset of examples, along normal sampling on the rest of the training set - provides for faster learning and better performance. This highlights that the benefits of repetition can outweigh those of data diversity. These datasets and problems provide a controlled setting to shed light on the still poorly understood interplay between generalization and memorization in deep learning.

Strong Model Collapse

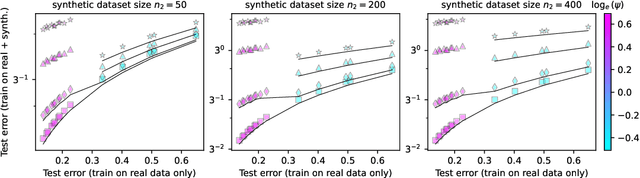
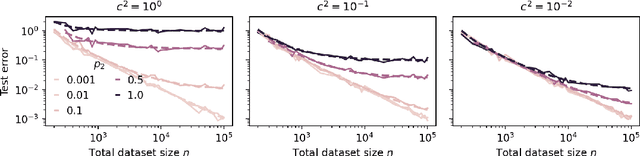
Within the scaling laws paradigm, which underpins the training of large neural networks like ChatGPT and Llama, we consider a supervised regression setting and establish the existance of a strong form of the model collapse phenomenon, a critical performance degradation due to synthetic data in the training corpus. Our results show that even the smallest fraction of synthetic data (e.g., as little as 1\% of the total training dataset) can still lead to model collapse: larger and larger training sets do not enhance performance. We further investigate whether increasing model size, an approach aligned with current trends in training large language models, exacerbates or mitigates model collapse. In a simplified regime where neural networks are approximated via random projections of tunable size, we both theoretically and empirically show that larger models can amplify model collapse. Interestingly, our theory also indicates that, beyond the interpolation threshold (which can be extremely high for very large datasets), larger models may mitigate the collapse, although they do not entirely prevent it. Our theoretical findings are empirically verified through experiments on language models and feed-forward neural networks for images.

Mission Impossible: A Statistical Perspective on Jailbreaking LLMs

Large language models (LLMs) are trained on a deluge of text data with limited quality control. As a result, LLMs can exhibit unintended or even harmful behaviours, such as leaking information, fake news or hate speech. Countermeasures, commonly referred to as preference alignment, include fine-tuning the pretrained LLMs with carefully crafted text examples of desired behaviour. Even then, empirical evidence shows preference aligned LLMs can be enticed to harmful behaviour. This so called jailbreaking of LLMs is typically achieved by adversarially modifying the input prompt to the LLM. Our paper provides theoretical insights into the phenomenon of preference alignment and jailbreaking from a statistical perspective. Under our framework, we first show that pretrained LLMs will mimic harmful behaviour if present in the training corpus. Under that same framework, we then introduce a statistical notion of alignment, and lower-bound the jailbreaking probability, showing that it is unpreventable under reasonable assumptions. Based on our insights, we propose an alteration to the currently prevalent alignment strategy RLHF. Specifically, we introduce a simple modification to the RLHF objective, we call E-RLHF, that aims to increase the likelihood of safe responses. E-RLHF brings no additional training cost, and is compatible with other methods. Empirically, we demonstrate that E-RLHF outperforms RLHF on all alignment problems put forward by the AdvBench and HarmBench project without sacrificing model performance as measured by the MT-Bench project.