PILAF: Optimal Human Preference Sampling for Reward Modeling

As large language models increasingly drive real-world applications, aligning them with human values becomes paramount. Reinforcement Learning from Human Feedback (RLHF) has emerged as a key technique, translating preference data into reward models when oracle human values remain inaccessible. In practice, RLHF mostly relies on approximate reward models, which may not consistently guide the policy toward maximizing the underlying human values. We propose Policy-Interpolated Learning for Aligned Feedback (PILAF), a novel response sampling strategy for preference labeling that explicitly aligns preference learning with maximizing the underlying oracle reward. PILAF is theoretically grounded, demonstrating optimality from both an optimization and a statistical perspective. The method is straightforward to implement and demonstrates strong performance in iterative and online RLHF settings where feedback curation is critical.

Spend Wisely: Maximizing Post-Training Gains in Iterative Synthetic Data Boostrapping

Modern foundation models often undergo iterative ``bootstrapping'' in their post-training phase: a model generates synthetic data, an external verifier filters out low-quality samples, and the high-quality subset is used for further fine-tuning. Over multiple iterations, the model's performance improves--raising a crucial question: how should the total budget on generation and training be allocated across iterations to maximize final performance? In this work, we develop a theoretical framework to analyze budget allocation strategies. Specifically, we show that constant policies fail to converge with high probability, while increasing policies--particularly exponential growth policies--exhibit significant theoretical advantages. Experiments on image denoising with diffusion probabilistic models and math reasoning with large language models show that both exponential and polynomial growth policies consistently outperform constant policies, with exponential policies often providing more stable performance.

Strong Model Collapse

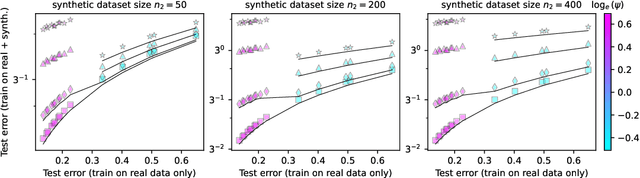
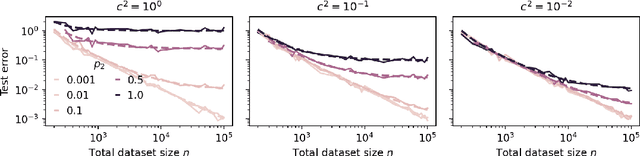
Within the scaling laws paradigm, which underpins the training of large neural networks like ChatGPT and Llama, we consider a supervised regression setting and establish the existance of a strong form of the model collapse phenomenon, a critical performance degradation due to synthetic data in the training corpus. Our results show that even the smallest fraction of synthetic data (e.g., as little as 1\% of the total training dataset) can still lead to model collapse: larger and larger training sets do not enhance performance. We further investigate whether increasing model size, an approach aligned with current trends in training large language models, exacerbates or mitigates model collapse. In a simplified regime where neural networks are approximated via random projections of tunable size, we both theoretically and empirically show that larger models can amplify model collapse. Interestingly, our theory also indicates that, beyond the interpolation threshold (which can be extremely high for very large datasets), larger models may mitigate the collapse, although they do not entirely prevent it. Our theoretical findings are empirically verified through experiments on language models and feed-forward neural networks for images.

Beyond Model Collapse: Scaling Up with Synthesized Data Requires Reinforcement

Synthesized data from generative models is increasingly considered as an alternative to human-annotated data for fine-tuning Large Language Models. This raises concerns about model collapse: a drop in performance of models fine-tuned on generated data. Considering that it is easier for both humans and machines to tell between good and bad examples than to generate high-quality samples, we investigate the use of feedback on synthesized data to prevent model collapse. We derive theoretical conditions under which a Gaussian mixture classification model can achieve asymptotically optimal performance when trained on feedback-augmented synthesized data, and provide supporting simulations for finite regimes. We illustrate our theoretical predictions on two practical problems: computing matrix eigenvalues with transformers and news summarization with large language models, which both undergo model collapse when trained on model-generated data. We show that training from feedback-augmented synthesized data, either by pruning incorrect predictions or by selecting the best of several guesses, can prevent model collapse, validating popular approaches like RLHF.

Attacking Bayes: On the Adversarial Robustness of Bayesian Neural Networks

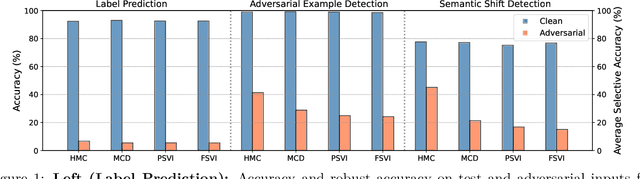
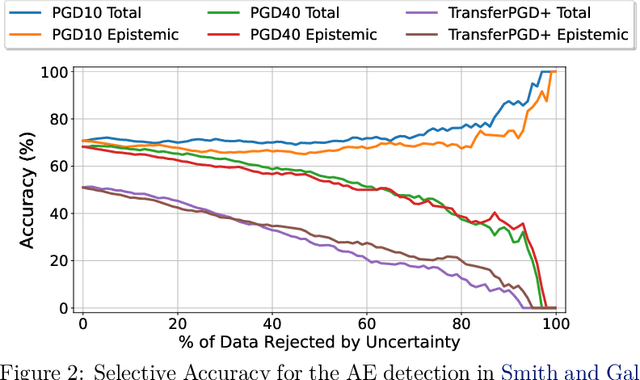
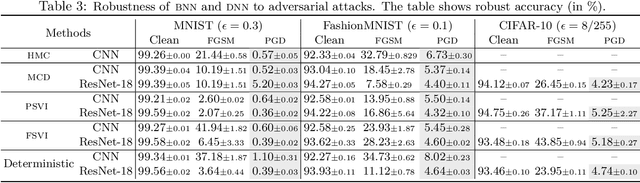
Adversarial examples have been shown to cause neural networks to fail on a wide range of vision and language tasks, but recent work has claimed that Bayesian neural networks (BNNs) are inherently robust to adversarial perturbations. In this work, we examine this claim. To study the adversarial robustness of BNNs, we investigate whether it is possible to successfully break state-of-the-art BNN inference methods and prediction pipelines using even relatively unsophisticated attacks for three tasks: (1) label prediction under the posterior predictive mean, (2) adversarial example detection with Bayesian predictive uncertainty, and (3) semantic shift detection. We find that BNNs trained with state-of-the-art approximate inference methods, and even BNNs trained with Hamiltonian Monte Carlo, are highly susceptible to adversarial attacks. We also identify various conceptual and experimental errors in previous works that claimed inherent adversarial robustness of BNNs and conclusively demonstrate that BNNs and uncertainty-aware Bayesian prediction pipelines are not inherently robust against adversarial attacks.

Do Efficient Transformers Really Save Computation?

As transformer-based language models are trained on increasingly large datasets and with vast numbers of parameters, finding more efficient alternatives to the standard Transformer has become very valuable. While many efficient Transformers and Transformer alternatives have been proposed, none provide theoretical guarantees that they are a suitable replacement for the standard Transformer. This makes it challenging to identify when to use a specific model and what directions to prioritize for further investigation. In this paper, we aim to understand the capabilities and limitations of efficient Transformers, specifically the Sparse Transformer and the Linear Transformer. We focus on their reasoning capability as exhibited by Chain-of-Thought (CoT) prompts and follow previous works to model them as Dynamic Programming (DP) problems. Our results show that while these models are expressive enough to solve general DP tasks, contrary to expectations, they require a model size that scales with the problem size. Nonetheless, we identify a class of DP problems for which these models can be more efficient than the standard Transformer. We confirm our theoretical results through experiments on representative DP tasks, adding to the understanding of efficient Transformers' practical strengths and weaknesses.

Model Collapse Demystified: The Case of Regression

In the era of large language models like ChatGPT, the phenomenon of "model collapse" refers to the situation whereby as a model is trained recursively on data generated from previous generations of itself over time, its performance degrades until the model eventually becomes completely useless, i.e the model collapses. In this work, we study this phenomenon in the simplified setting of kernel regression and obtain results which show a clear crossover between where the model can cope with fake data, and a regime where the model's performance completely collapses. Under polynomial decaying spectral and source conditions, we obtain modified scaling laws which exhibit new crossover phenomena from fast to slow rates. We also propose a simple strategy based on adaptive regularization to mitigate model collapse. Our theoretical results are validated with experiments.

A Tale of Tails: Model Collapse as a Change of Scaling Laws

As AI model size grows, neural scaling laws have become a crucial tool to predict the improvements of large models when increasing capacity and the size of original (human or natural) training data. Yet, the widespread use of popular models means that the ecosystem of online data and text will co-evolve to progressively contain increased amounts of synthesized data. In this paper we ask: How will the scaling laws change in the inevitable regime where synthetic data makes its way into the training corpus? Will future models, still improve, or be doomed to degenerate up to total (model) collapse? We develop a theoretical framework of model collapse through the lens of scaling laws. We discover a wide range of decay phenomena, analyzing loss of scaling, shifted scaling with number of generations, the ''un-learning" of skills, and grokking when mixing human and synthesized data. Our theory is validated by large-scale experiments with a transformer on an arithmetic task and text generation using the large language model Llama2.

Embarassingly Simple Dataset Distillation

Dataset distillation extracts a small set of synthetic training samples from a large dataset with the goal of achieving competitive performance on test data when trained on this sample. In this work, we tackle dataset distillation at its core by treating it directly as a bilevel optimization problem. Re-examining the foundational back-propagation through time method, we study the pronounced variance in the gradients, computational burden, and long-term dependencies. We introduce an improved method: Random Truncated Backpropagation Through Time (RaT-BPTT) to address them. RaT-BPTT incorporates a truncation coupled with a random window, effectively stabilizing the gradients and speeding up the optimization while covering long dependencies. This allows us to establish new state-of-the-art for a variety of standard dataset benchmarks. A deeper dive into the nature of distilled data unveils pronounced intercorrelation. In particular, subsets of distilled datasets tend to exhibit much worse performance than directly distilled smaller datasets of the same size. Leveraging RaT-BPTT, we devise a boosting mechanism that generates distilled datasets that contain subsets with near optimal performance across different data budgets.

Transferred Discrepancy: Quantifying the Difference Between Representations

Understanding what information neural networks capture is an essential problem in deep learning, and studying whether different models capture similar features is an initial step to achieve this goal. Previous works sought to define metrics over the feature matrices to measure the difference between two models. However, different metrics sometimes lead to contradictory conclusions, and there has been no consensus on which metric is suitable to use in practice. In this work, we propose a novel metric that goes beyond previous approaches. Recall that one of the most practical scenarios of using the learned representations is to apply them to downstream tasks. We argue that we should design the metric based on a similar principle. For that, we introduce the transferred discrepancy (TD), a new metric that defines the difference between two representations based on their downstream-task performance. Through an asymptotic analysis, we show how TD correlates with downstream tasks and the necessity to define metrics in such a task-dependent fashion. In particular, we also show that under specific conditions, the TD metric is closely related to previous metrics. Our experiments show that TD can provide fine-grained information for varied downstream tasks, and for the models trained from different initializations, the learned features are not the same in terms of downstream-task predictions. We find that TD may also be used to evaluate the effectiveness of different training strategies. For example, we demonstrate that the models trained with proper data augmentations that improve the generalization capture more similar features in terms of TD, while those with data augmentations that hurt the generalization will not. This suggests a training strategy that leads to more robust representation also trains models that generalize better.