Spectrally Transformed Kernel Regression

Unlabeled data is a key component of modern machine learning. In general, the role of unlabeled data is to impose a form of smoothness, usually from the similarity information encoded in a base kernel, such as the $\epsilon$-neighbor kernel or the adjacency matrix of a graph. This work revisits the classical idea of spectrally transformed kernel regression (STKR), and provides a new class of general and scalable STKR estimators able to leverage unlabeled data. Intuitively, via spectral transformation, STKR exploits the data distribution for which unlabeled data can provide additional information. First, we show that STKR is a principled and general approach, by characterizing a universal type of "target smoothness", and proving that any sufficiently smooth function can be learned by STKR. Second, we provide scalable STKR implementations for the inductive setting and a general transformation function, while prior work is mostly limited to the transductive setting. Third, we derive statistical guarantees for two scenarios: STKR with a known polynomial transformation, and STKR with kernel PCA when the transformation is unknown. Overall, we believe that this work helps deepen our understanding of how to work with unlabeled data, and its generality makes it easier to inspire new methods.

Responsible AI (RAI) Games and Ensembles

Several recent works have studied the societal effects of AI; these include issues such as fairness, robustness, and safety. In many of these objectives, a learner seeks to minimize its worst-case loss over a set of predefined distributions (known as uncertainty sets), with usual examples being perturbed versions of the empirical distribution. In other words, aforementioned problems can be written as min-max problems over these uncertainty sets. In this work, we provide a general framework for studying these problems, which we refer to as Responsible AI (RAI) games. We provide two classes of algorithms for solving these games: (a) game-play based algorithms, and (b) greedy stagewise estimation algorithms. The former class is motivated by online learning and game theory, whereas the latter class is motivated by the classical statistical literature on boosting, and regression. We empirically demonstrate the applicability and competitive performance of our techniques for solving several RAI problems, particularly around subpopulation shift.

Understanding Augmentation-based Self-Supervised Representation Learning via RKHS Approximation

Good data augmentation is one of the key factors that lead to the empirical success of self-supervised representation learning such as contrastive learning and masked language modeling, yet theoretical understanding of its role in learning good representations remains limited. Recent work has built the connection between self-supervised learning and approximating the top eigenspace of a graph Laplacian operator. Learning a linear probe on top of such features can naturally be connected to RKHS regression. In this work, we use this insight to perform a statistical analysis of augmentation-based pretraining. We start from the isometry property, a key geometric characterization of the target function given by the augmentation. Our first main theorem provides, for an arbitrary encoder, near tight bounds for both the estimation error incurred by fitting the linear probe on top of the encoder, and the approximation error entailed by the fitness of the RKHS the encoder learns. Our second main theorem specifically addresses the case where the encoder extracts the top-d eigenspace of a Monte-Carlo approximation of the underlying kernel with the finite pretraining samples. Our analysis completely disentangles the effects of the model and the augmentation. A key ingredient in our analysis is the augmentation complexity, which we use to quantitatively compare different augmentations and analyze their impact on downstream performance on synthetic and real datasets.

Characterizing Out-of-Distribution Error via Optimal Transport

Out-of-distribution (OOD) data poses serious challenges in deployed machine learning models, so methods of predicting a model's performance on OOD data without labels are important for machine learning safety. While a number of methods have been proposed by prior work, they often underestimate the actual error, sometimes by a large margin, which greatly impacts their applicability to real tasks. In this work, we identify pseudo-label shift, or the difference between the predicted and true OOD label distributions, as a key indicator to this underestimation. Based on this observation, we introduce a novel method for estimating model performance by leveraging optimal transport theory, Confidence Optimal Transport (COT), and show that it provably provides more robust error estimates in the presence of pseudo-label shift. Additionally, we introduce an empirically-motivated variant of COT, Confidence Optimal Transport with Thresholding (COTT), which applies thresholding to the individual transport costs and further improves the accuracy of COT's error estimates. We evaluate COT and COTT on a variety of standard benchmarks that induce various types of distribution shift -- synthetic, novel subpopulation, and natural -- and show that our approaches significantly outperform existing state-of-the-art methods with an up to 3x lower prediction error.

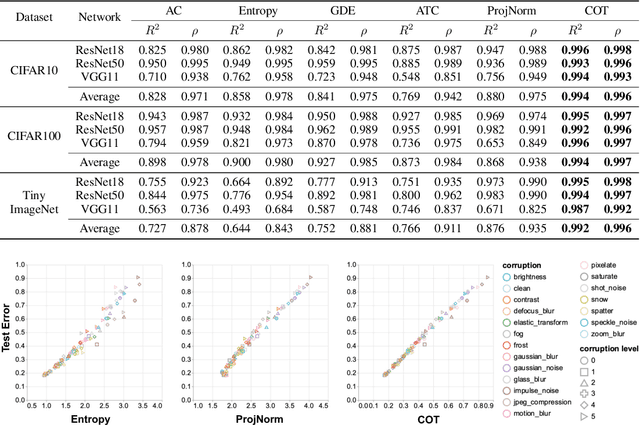
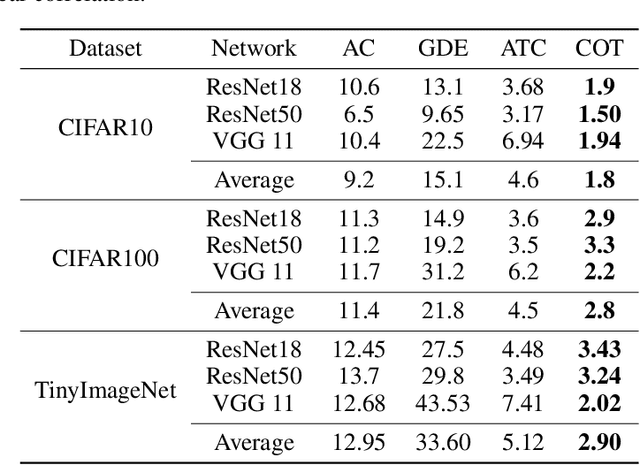
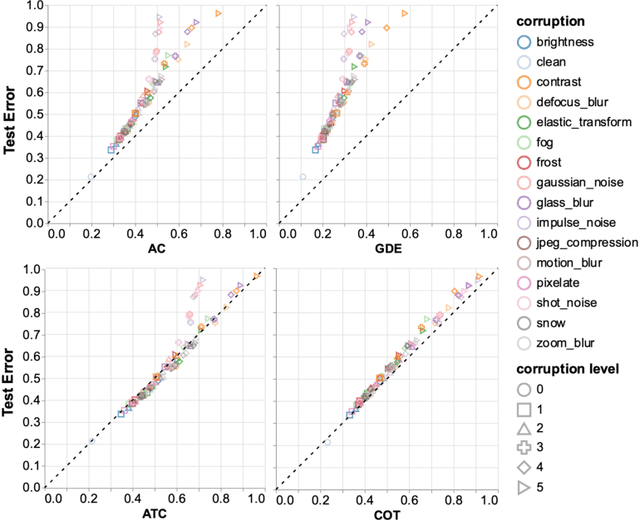
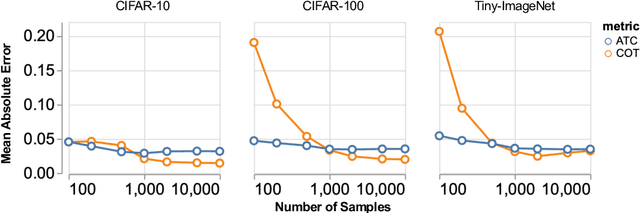
Predicting Out-of-Distribution Error with Confidence Optimal Transport

Out-of-distribution (OOD) data poses serious challenges in deployed machine learning models as even subtle changes could incur significant performance drops. Being able to estimate a model's performance on test data is important in practice as it indicates when to trust to model's decisions. We present a simple yet effective method to predict a model's performance on an unknown distribution without any addition annotation. Our approach is rooted in the Optimal Transport theory, viewing test samples' output softmax scores from deep neural networks as empirical samples from an unknown distribution. We show that our method, Confidence Optimal Transport (COT), provides robust estimates of a model's performance on a target domain. Despite its simplicity, our method achieves state-of-the-art results on three benchmark datasets and outperforms existing methods by a large margin.

Understanding Why Generalized Reweighting Does Not Improve Over ERM

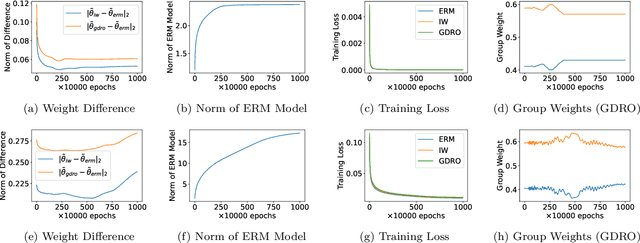
Empirical risk minimization (ERM) is known in practice to be non-robust to distributional shift where the training and the test distributions are different. A suite of approaches, such as importance weighting, and variants of distributionally robust optimization (DRO), have been proposed to solve this problem. But a line of recent work has empirically shown that these approaches do not significantly improve over ERM in real applications with distribution shift. The goal of this work is to obtain a comprehensive theoretical understanding of this intriguing phenomenon. We first posit the class of Generalized Reweighting (GRW) algorithms, as a broad category of approaches that iteratively update model parameters based on iterative reweighting of the training samples. We show that when overparameterized models are trained under GRW, the resulting models are close to that obtained by ERM. We also show that adding small regularization which does not greatly affect the empirical training accuracy does not help. Together, our results show that a broad category of what we term GRW approaches are not able to achieve distributionally robust generalization. Our work thus has the following sobering takeaway: to make progress towards distributionally robust generalization, we either have to develop non-GRW approaches, or perhaps devise novel classification/regression loss functions that are adapted to the class of GRW approaches.

Boosted CVaR Classification

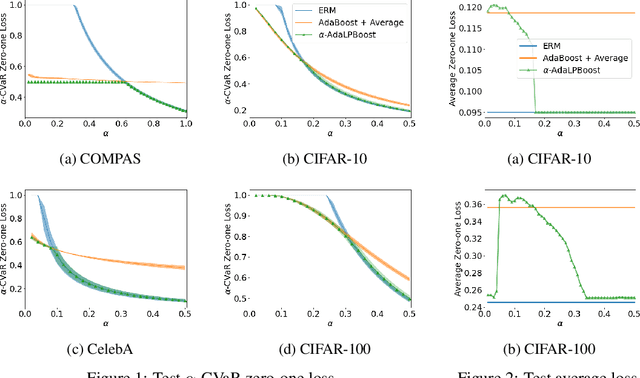
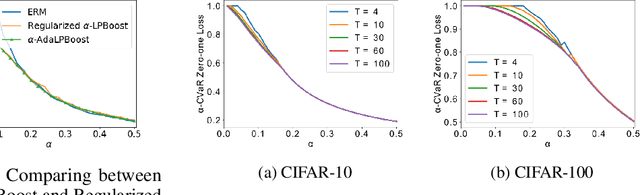
Many modern machine learning tasks require models with high tail performance, i.e. high performance over the worst-off samples in the dataset. This problem has been widely studied in fields such as algorithmic fairness, class imbalance, and risk-sensitive decision making. A popular approach to maximize the model's tail performance is to minimize the CVaR (Conditional Value at Risk) loss, which computes the average risk over the tails of the loss. However, for classification tasks where models are evaluated by the zero-one loss, we show that if the classifiers are deterministic, then the minimizer of the average zero-one loss also minimizes the CVaR zero-one loss, suggesting that CVaR loss minimization is not helpful without additional assumptions. We circumvent this negative result by minimizing the CVaR loss over randomized classifiers, for which the minimizers of the average zero-one loss and the CVaR zero-one loss are no longer the same, so minimizing the latter can lead to better tail performance. To learn such randomized classifiers, we propose the Boosted CVaR Classification framework which is motivated by a direct relationship between CVaR and a classical boosting algorithm called LPBoost. Based on this framework, we design an algorithm called $\alpha$-AdaLPBoost. We empirically evaluate our proposed algorithm on four benchmark datasets and show that it achieves higher tail performance than deterministic model training methods.

DORO: Distributional and Outlier Robust Optimization

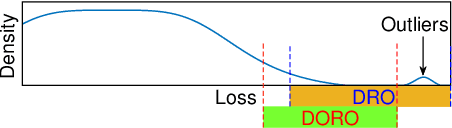
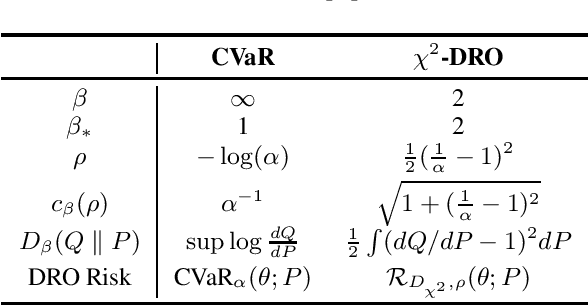
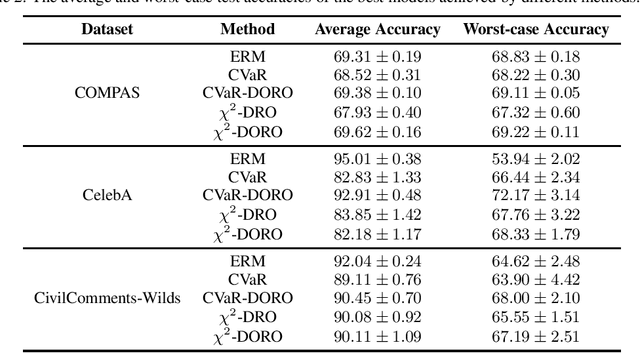
Many machine learning tasks involve subpopulation shift where the testing data distribution is a subpopulation of the training distribution. For such settings, a line of recent work has proposed the use of a variant of empirical risk minimization(ERM) known as distributionally robust optimization (DRO). In this work, we apply DRO to real, large-scale tasks with subpopulation shift, and observe that DRO performs relatively poorly, and moreover has severe instability. We identify one direct cause of this phenomenon: sensitivity of DRO to outliers in the datasets. To resolve this issue, we propose the framework of DORO, for Distributional and Outlier Robust Optimization. At the core of this approach is a refined risk function which prevents DRO from overfitting to potential outliers. We instantiate DORO for the Cressie-Read family of R\'enyi divergence, and delve into two specific instances of this family: CVaR and $\chi^2$-DRO. We theoretically prove the effectiveness of the proposed method, and empirically show that DORO improves the performance and stability of DRO with experiments on large modern datasets, thereby positively addressing the open question raised by Hashimoto et al., 2018.

Transferred Discrepancy: Quantifying the Difference Between Representations

Understanding what information neural networks capture is an essential problem in deep learning, and studying whether different models capture similar features is an initial step to achieve this goal. Previous works sought to define metrics over the feature matrices to measure the difference between two models. However, different metrics sometimes lead to contradictory conclusions, and there has been no consensus on which metric is suitable to use in practice. In this work, we propose a novel metric that goes beyond previous approaches. Recall that one of the most practical scenarios of using the learned representations is to apply them to downstream tasks. We argue that we should design the metric based on a similar principle. For that, we introduce the transferred discrepancy (TD), a new metric that defines the difference between two representations based on their downstream-task performance. Through an asymptotic analysis, we show how TD correlates with downstream tasks and the necessity to define metrics in such a task-dependent fashion. In particular, we also show that under specific conditions, the TD metric is closely related to previous metrics. Our experiments show that TD can provide fine-grained information for varied downstream tasks, and for the models trained from different initializations, the learned features are not the same in terms of downstream-task predictions. We find that TD may also be used to evaluate the effectiveness of different training strategies. For example, we demonstrate that the models trained with proper data augmentations that improve the generalization capture more similar features in terms of TD, while those with data augmentations that hurt the generalization will not. This suggests a training strategy that leads to more robust representation also trains models that generalize better.

MACER: Attack-free and Scalable Robust Training via Maximizing Certified Radius

Adversarial training is one of the most popular ways to learn robust models but is usually attack-dependent and time costly. In this paper, we propose the MACER algorithm, which learns robust models without using adversarial training but performs better than all existing provable l2-defenses. Recent work shows that randomized smoothing can be used to provide a certified l2 radius to smoothed classifiers, and our algorithm trains provably robust smoothed classifiers via MAximizing the CErtified Radius (MACER). The attack-free characteristic makes MACER faster to train and easier to optimize. In our experiments, we show that our method can be applied to modern deep neural networks on a wide range of datasets, including Cifar-10, ImageNet, MNIST, and SVHN. For all tasks, MACER spends less training time than state-of-the-art adversarial training algorithms, and the learned models achieve larger average certified radius.