Distributional Adversarial Loss

A major challenge in defending against adversarial attacks is the enormous space of possible attacks that even a simple adversary might perform. To address this, prior work has proposed a variety of defenses that effectively reduce the size of this space. These include randomized smoothing methods that add noise to the input to take away some of the adversary's impact. Another approach is input discretization which limits the adversary's possible number of actions. Motivated by these two approaches, we introduce a new notion of adversarial loss which we call distributional adversarial loss, to unify these two forms of effectively weakening an adversary. In this notion, we assume for each original example, the allowed adversarial perturbation set is a family of distributions (e.g., induced by a smoothing procedure), and the adversarial loss over each example is the maximum loss over all the associated distributions. The goal is to minimize the overall adversarial loss. We show generalization guarantees for our notion of adversarial loss in terms of the VC-dimension of the hypothesis class and the size of the set of allowed adversarial distributions associated with each input. We also investigate the role of randomness in achieving robustness against adversarial attacks in the methods described above. We show a general derandomization technique that preserves the extent of a randomized classifier's robustness against adversarial attacks. We corroborate the procedure experimentally via derandomizing the Random Projection Filters framework of \cite{dong2023adversarial}. Our procedure also improves the robustness of the model against various adversarial attacks.

Low-Rank Adaptation of Time Series Foundational Models for Out-of-Domain Modality Forecasting

Low-Rank Adaptation (LoRA) is a widely used technique for fine-tuning large pre-trained or foundational models across different modalities and tasks. However, its application to time series data, particularly within foundational models, remains underexplored. This paper examines the impact of LoRA on contemporary time series foundational models: Lag-Llama, MOIRAI, and Chronos. We demonstrate LoRA's fine-tuning potential for forecasting the vital signs of sepsis patients in intensive care units (ICUs), emphasizing the models' adaptability to previously unseen, out-of-domain modalities. Integrating LoRA aims to enhance forecasting performance while reducing inefficiencies associated with fine-tuning large models on limited domain-specific data. Our experiments show that LoRA fine-tuning of time series foundational models significantly improves forecasting, achieving results comparable to state-of-the-art models trained from scratch on similar modalities. We conduct comprehensive ablation studies to demonstrate the trade-offs between the number of tunable parameters and forecasting performance and assess the impact of varying LoRA matrix ranks on model performance.

Interpretable Vital Sign Forecasting with Model Agnostic Attention Maps

Sepsis is a leading cause of mortality in intensive care units (ICUs), representing a substantial medical challenge. The complexity of analyzing diverse vital signs to predict sepsis further aggravates this issue. While deep learning techniques have been advanced for early sepsis prediction, their 'black-box' nature obscures the internal logic, impairing interpretability in critical settings like ICUs. This paper introduces a framework that combines a deep learning model with an attention mechanism that highlights the critical time steps in the forecasting process, thus improving model interpretability and supporting clinical decision-making. We show that the attention mechanism could be adapted to various black box time series forecasting models such as N-HiTS and N-BEATS. Our method preserves the accuracy of conventional deep learning models while enhancing interpretability through attention-weight-generated heatmaps. We evaluated our model on the eICU-CRD dataset, focusing on forecasting vital signs for sepsis patients. We assessed its performance using mean squared error (MSE) and dynamic time warping (DTW) metrics. We explored the attention maps of N-HiTS and N-BEATS, examining the differences in their performance and identifying crucial factors influencing vital sign forecasting.

Vital Sign Forecasting for Sepsis Patients in ICUs

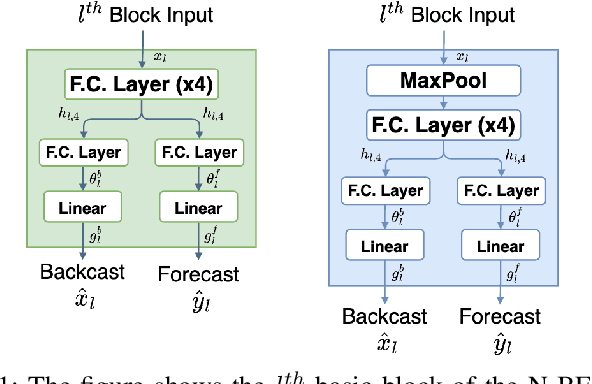
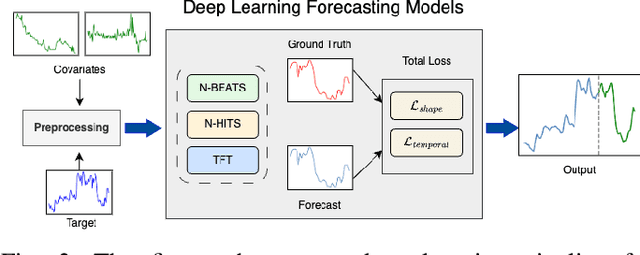
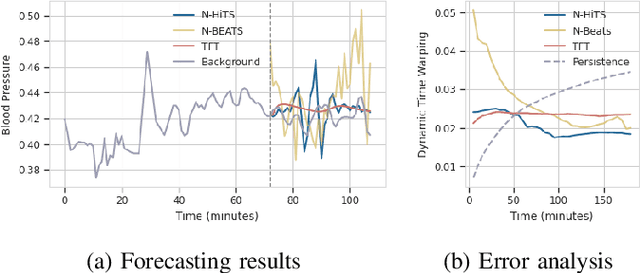
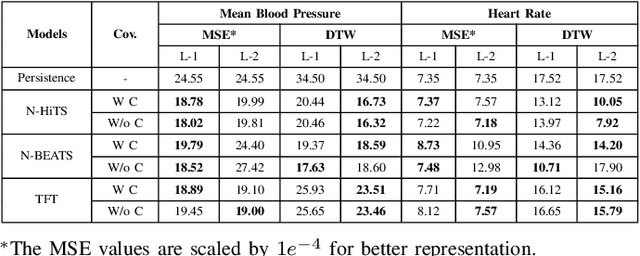
Sepsis and septic shock are a critical medical condition affecting millions globally, with a substantial mortality rate. This paper uses state-of-the-art deep learning (DL) architectures to introduce a multi-step forecasting system to predict vital signs indicative of septic shock progression in Intensive Care Units (ICUs). Our approach utilizes a short window of historical vital sign data to forecast future physiological conditions. We introduce a DL-based vital sign forecasting system that predicts up to 3 hours of future vital signs from 6 hours of past data. We further adopt the DILATE loss function to capture better the shape and temporal dynamics of vital signs, which are critical for clinical decision-making. We compare three DL models, N-BEATS, N-HiTS, and Temporal Fusion Transformer (TFT), using the publicly available eICU Collaborative Research Database (eICU-CRD), highlighting their forecasting capabilities in a critical care setting. We evaluate the performance of our models using mean squared error (MSE) and dynamic time warping (DTW) metrics. Our findings show that while TFT excels in capturing overall trends, N-HiTS is superior in retaining short-term fluctuations within a predefined range. This paper demonstrates the potential of deep learning in transforming the monitoring systems in ICUs, potentially leading to significant improvements in patient care and outcomes by accurately forecasting vital signs to assist healthcare providers in detecting early signs of physiological instability and anticipating septic shock.

Understanding Why Generalized Reweighting Does Not Improve Over ERM

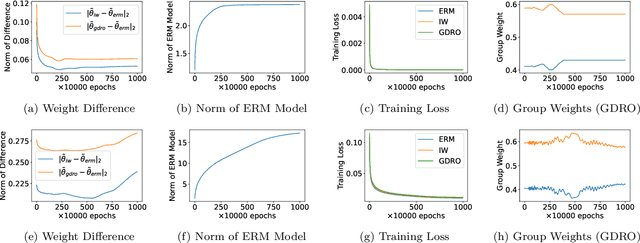
Empirical risk minimization (ERM) is known in practice to be non-robust to distributional shift where the training and the test distributions are different. A suite of approaches, such as importance weighting, and variants of distributionally robust optimization (DRO), have been proposed to solve this problem. But a line of recent work has empirically shown that these approaches do not significantly improve over ERM in real applications with distribution shift. The goal of this work is to obtain a comprehensive theoretical understanding of this intriguing phenomenon. We first posit the class of Generalized Reweighting (GRW) algorithms, as a broad category of approaches that iteratively update model parameters based on iterative reweighting of the training samples. We show that when overparameterized models are trained under GRW, the resulting models are close to that obtained by ERM. We also show that adding small regularization which does not greatly affect the empirical training accuracy does not help. Together, our results show that a broad category of what we term GRW approaches are not able to achieve distributionally robust generalization. Our work thus has the following sobering takeaway: to make progress towards distributionally robust generalization, we either have to develop non-GRW approaches, or perhaps devise novel classification/regression loss functions that are adapted to the class of GRW approaches.

Boosted CVaR Classification

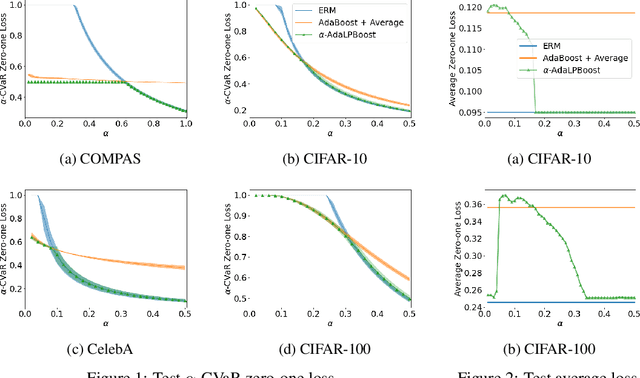
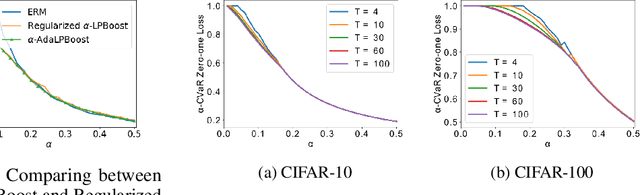
Many modern machine learning tasks require models with high tail performance, i.e. high performance over the worst-off samples in the dataset. This problem has been widely studied in fields such as algorithmic fairness, class imbalance, and risk-sensitive decision making. A popular approach to maximize the model's tail performance is to minimize the CVaR (Conditional Value at Risk) loss, which computes the average risk over the tails of the loss. However, for classification tasks where models are evaluated by the zero-one loss, we show that if the classifiers are deterministic, then the minimizer of the average zero-one loss also minimizes the CVaR zero-one loss, suggesting that CVaR loss minimization is not helpful without additional assumptions. We circumvent this negative result by minimizing the CVaR loss over randomized classifiers, for which the minimizers of the average zero-one loss and the CVaR zero-one loss are no longer the same, so minimizing the latter can lead to better tail performance. To learn such randomized classifiers, we propose the Boosted CVaR Classification framework which is motivated by a direct relationship between CVaR and a classical boosting algorithm called LPBoost. Based on this framework, we design an algorithm called $\alpha$-AdaLPBoost. We empirically evaluate our proposed algorithm on four benchmark datasets and show that it achieves higher tail performance than deterministic model training methods.

DORO: Distributional and Outlier Robust Optimization

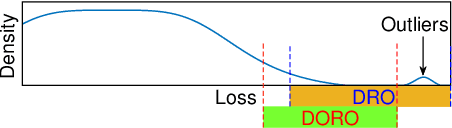
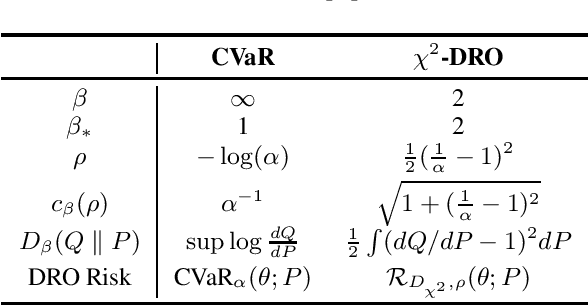
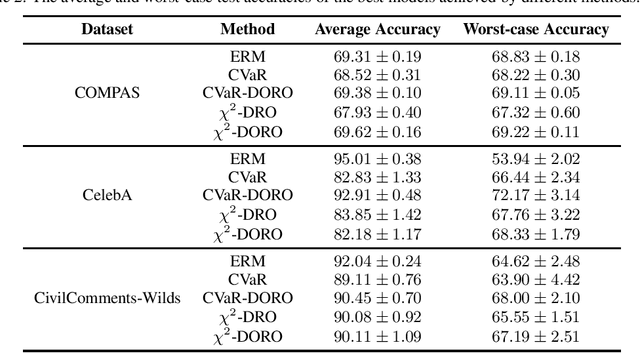
Many machine learning tasks involve subpopulation shift where the testing data distribution is a subpopulation of the training distribution. For such settings, a line of recent work has proposed the use of a variant of empirical risk minimization(ERM) known as distributionally robust optimization (DRO). In this work, we apply DRO to real, large-scale tasks with subpopulation shift, and observe that DRO performs relatively poorly, and moreover has severe instability. We identify one direct cause of this phenomenon: sensitivity of DRO to outliers in the datasets. To resolve this issue, we propose the framework of DORO, for Distributional and Outlier Robust Optimization. At the core of this approach is a refined risk function which prevents DRO from overfitting to potential outliers. We instantiate DORO for the Cressie-Read family of R\'enyi divergence, and delve into two specific instances of this family: CVaR and $\chi^2$-DRO. We theoretically prove the effectiveness of the proposed method, and empirically show that DORO improves the performance and stability of DRO with experiments on large modern datasets, thereby positively addressing the open question raised by Hashimoto et al., 2018.

Fundamental Limits and Tradeoffs in Invariant Representation Learning

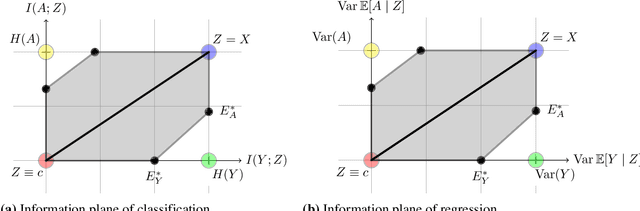
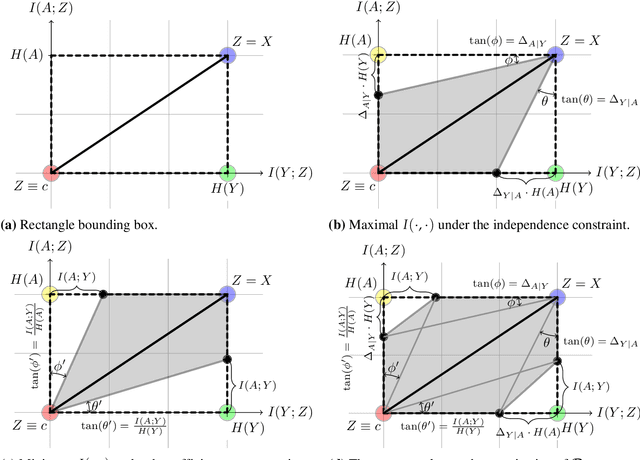
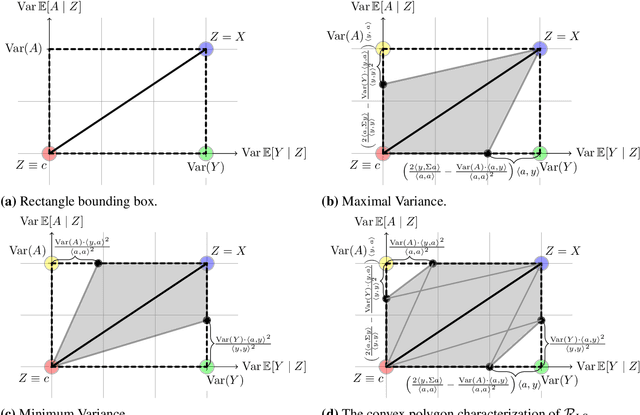
Many machine learning applications involve learning representations that achieve two competing goals: To maximize information or accuracy with respect to a subset of features (e.g.\ for prediction) while simultaneously maximizing invariance or independence with respect to another, potentially overlapping, subset of features (e.g.\ for fairness, privacy, etc). Typical examples include privacy-preserving learning, domain adaptation, and algorithmic fairness, just to name a few. In fact, all of the above problems admit a common minimax game-theoretic formulation, whose equilibrium represents a fundamental tradeoff between accuracy and invariance. Despite its abundant applications in the aforementioned domains, theoretical understanding on the limits and tradeoffs of invariant representations is severely lacking. In this paper, we provide an information-theoretic analysis of this general and important problem under both classification and regression settings. In both cases, we analyze the inherent tradeoffs between accuracy and invariance by providing a geometric characterization of the feasible region in the information plane, where we connect the geometric properties of this feasible region to the fundamental limitations of the tradeoff problem. In the regression setting, we also derive a tight lower bound on the Lagrangian objective that quantifies the tradeoff between accuracy and invariance. This lower bound leads to a better understanding of the tradeoff via the spectral properties of the joint distribution. In both cases, our results shed new light on this fundamental problem by providing insights on the interplay between accuracy and invariance. These results deepen our understanding of this fundamental problem and may be useful in guiding the design of adversarial representation learning algorithms.

Sharp Statistical Guarantees for Adversarially Robust Gaussian Classification

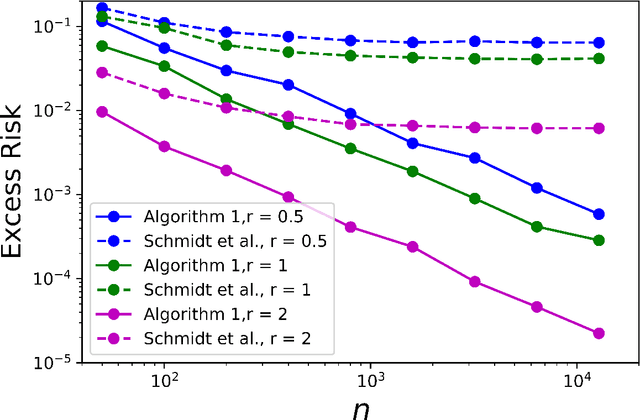
Adversarial robustness has become a fundamental requirement in modern machine learning applications. Yet, there has been surprisingly little statistical understanding so far. In this paper, we provide the first result of the optimal minimax guarantees for the excess risk for adversarially robust classification, under Gaussian mixture model proposed by \cite{schmidt2018adversarially}. The results are stated in terms of the Adversarial Signal-to-Noise Ratio (AdvSNR), which generalizes a similar notion for standard linear classification to the adversarial setting. For the Gaussian mixtures with AdvSNR value of $r$, we establish an excess risk lower bound of order $\Theta(e^{-(\frac{1}{8}+o(1)) r^2} \frac{d}{n})$ and design a computationally efficient estimator that achieves this optimal rate. Our results built upon minimal set of assumptions while cover a wide spectrum of adversarial perturbations including $\ell_p$ balls for any $p \ge 1$.

Class-Weighted Classification: Trade-offs and Robust Approaches

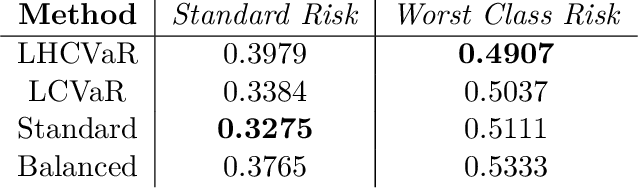
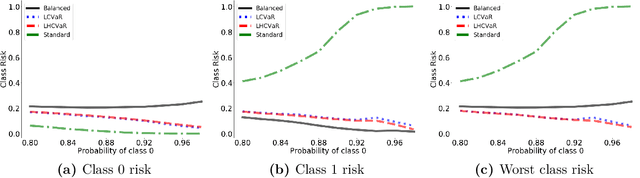
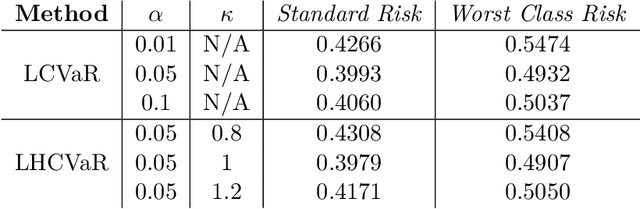
We address imbalanced classification, the problem in which a label may have low marginal probability relative to other labels, by weighting losses according to the correct class. First, we examine the convergence rates of the expected excess weighted risk of plug-in classifiers where the weighting for the plug-in classifier and the risk may be different. This leads to irreducible errors that do not converge to the weighted Bayes risk, which motivates our consideration of robust risks. We define a robust risk that minimizes risk over a set of weightings and show excess risk bounds for this problem. Finally, we show that particular choices of the weighting set leads to a special instance of conditional value at risk (CVaR) from stochastic programming, which we call label conditional value at risk (LCVaR). Additionally, we generalize this weighting to derive a new robust risk problem that we call label heterogeneous conditional value at risk (LHCVaR). Finally, we empirically demonstrate the efficacy of LCVaR and LHCVaR on improving class conditional risks.