Replicable Online Learning

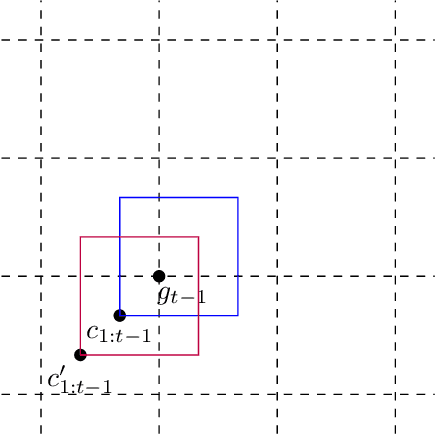
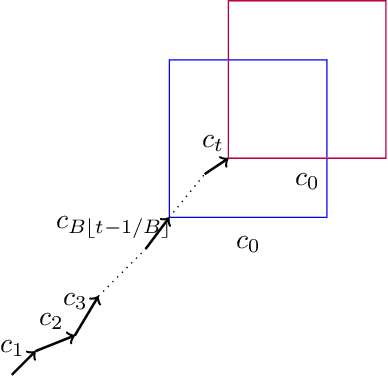
We investigate the concept of algorithmic replicability introduced by Impagliazzo et al. 2022, Ghazi et al. 2021, Ahn et al. 2024 in an online setting. In our model, the input sequence received by the online learner is generated from time-varying distributions chosen by an adversary (obliviously). Our objective is to design low-regret online algorithms that, with high probability, produce the exact same sequence of actions when run on two independently sampled input sequences generated as described above. We refer to such algorithms as adversarially replicable. Previous works (such as Esfandiari et al. 2022) explored replicability in the online setting under inputs generated independently from a fixed distribution; we term this notion as iid-replicability. Our model generalizes to capture both adversarial and iid input sequences, as well as their mixtures, which can be modeled by setting certain distributions as point-masses. We demonstrate adversarially replicable online learning algorithms for online linear optimization and the experts problem that achieve sub-linear regret. Additionally, we propose a general framework for converting an online learner into an adversarially replicable one within our setting, bounding the new regret in terms of the original algorithm's regret. We also present a nearly optimal (in terms of regret) iid-replicable online algorithm for the experts problem, highlighting the distinction between the iid and adversarial notions of replicability. Finally, we establish lower bounds on the regret (in terms of the replicability parameter and time) that any replicable online algorithm must incur.

Distributional Adversarial Loss

A major challenge in defending against adversarial attacks is the enormous space of possible attacks that even a simple adversary might perform. To address this, prior work has proposed a variety of defenses that effectively reduce the size of this space. These include randomized smoothing methods that add noise to the input to take away some of the adversary's impact. Another approach is input discretization which limits the adversary's possible number of actions. Motivated by these two approaches, we introduce a new notion of adversarial loss which we call distributional adversarial loss, to unify these two forms of effectively weakening an adversary. In this notion, we assume for each original example, the allowed adversarial perturbation set is a family of distributions (e.g., induced by a smoothing procedure), and the adversarial loss over each example is the maximum loss over all the associated distributions. The goal is to minimize the overall adversarial loss. We show generalization guarantees for our notion of adversarial loss in terms of the VC-dimension of the hypothesis class and the size of the set of allowed adversarial distributions associated with each input. We also investigate the role of randomness in achieving robustness against adversarial attacks in the methods described above. We show a general derandomization technique that preserves the extent of a randomized classifier's robustness against adversarial attacks. We corroborate the procedure experimentally via derandomizing the Random Projection Filters framework of \cite{dong2023adversarial}. Our procedure also improves the robustness of the model against various adversarial attacks.

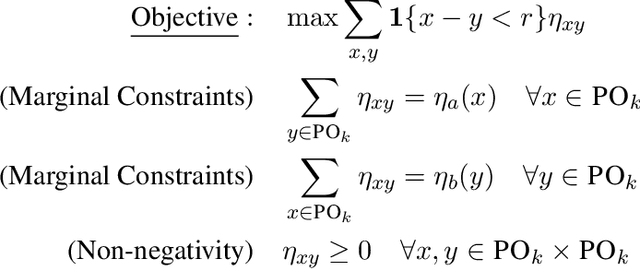
Limits of Approximating the Median Treatment Effect

Average Treatment Effect (ATE) estimation is a well-studied problem in causal inference. However, it does not necessarily capture the heterogeneity in the data, and several approaches have been proposed to tackle the issue, including estimating the Quantile Treatment Effects. In the finite population setting containing $n$ individuals, with treatment and control values denoted by the potential outcome vectors $\mathbf{a}, \mathbf{b}$, much of the prior work focused on estimating median$(\mathbf{a}) -$ median$(\mathbf{b})$, where median($\mathbf x$) denotes the median value in the sorted ordering of all the values in vector $\mathbf x$. It is known that estimating the difference of medians is easier than the desired estimand of median$(\mathbf{a-b})$, called the Median Treatment Effect (MTE). The fundamental problem of causal inference -- for every individual $i$, we can only observe one of the potential outcome values, i.e., either the value $a_i$ or $b_i$, but not both, makes estimating MTE particularly challenging. In this work, we argue that MTE is not estimable and detail a novel notion of approximation that relies on the sorted order of the values in $\mathbf{a-b}$. Next, we identify a quantity called variability that exactly captures the complexity of MTE estimation. By drawing connections to instance-optimality studied in theoretical computer science, we show that every algorithm for estimating the MTE obtains an approximation error that is no better than the error of an algorithm that computes variability. Finally, we provide a simple linear time algorithm for computing the variability exactly. Unlike much prior work, a particular highlight of our work is that we make no assumptions about how the potential outcome vectors are generated or how they are correlated, except that the potential outcome values are $k$-ary, i.e., take one of $k$ discrete values.