Revealing Positive and Negative Role Models to Help People Make Good Decisions

We consider a setting where agents take action by following their role models in a social network, and study strategies for a social planner to help agents by revealing whether the role models are positive or negative. Specifically, agents observe a local neighborhood of possible role models they can emulate, but do not know their true labels. Revealing a positive label encourages emulation, while revealing a negative one redirects agents toward alternative options. The social planner observes all labels, but operates under a limited disclosure budget that it selectively allocates to maximize social welfare (the expected number of agents who emulate adjacent positive role models). We consider both algorithms and hardness results for welfare maximization, and provide a sample-complexity guarantee when the planner observes a sampled subset of agents. We also consider fairness guarantees when agents belong to different groups. It is a technical challenge that the ability to reveal negative role models breaks submodularity. We thus introduce a proxy welfare function that remains submodular even when revealed targets include negative ones. When each agent has at most a constant number of negative target neighbors, we use this proxy to achieve a constant-factor approximation to the true optimal welfare gain. When agents belong to different groups, we also show that each group's welfare gain is within a constant factor of the optimum achievable if the full budget were allocated to that group. Beyond this basic model, we also propose an intervention model that directly connects high-risk agents to positive role models, and a coverage radius model that expands the visibility of selected positive role models. Lastly, we conduct extensive experiments on four real-world datasets to support our theoretical results and assess the effectiveness of the proposed algorithms.

Online Learnability of Chain-of-Thought Verifiers: Soundness and Completeness Trade-offs

Large language models with chain-of-thought generation have demonstrated great potential for producing complex mathematical proofs. However, their reasoning can often go astray, leading to increasing interest in formal and learned verifiers. A major challenge in learning verifiers, especially when their output will be used by the prover, is that this feedback loop may produce substantial distribution shift. Motivated by this challenge, we propose an online learning framework for learning chain-of-thought verifiers that, given a problem and a sequence of reasoning steps, check the correctness of the solution. Highlighting the asymmetric role of soundness (failure in catching errors in a proof) and completeness (flagging correct proofs as wrong) mistakes of the verifier, we introduce novel extensions of the Littlestone dimension which tightly characterize the mistake bounds for learning a verifier in the realizable setting. We provide optimal algorithms for finding the Pareto-frontier (the smallest total number of mistakes given a budget of soundness mistakes) as well as minimizing a linear combination of asymmetric costs. We further show how our learned verifiers can be used to boost the accuracy of a collection of weak provers, and enable generation of proofs beyond what they were trained on. With the mild assumption that one of the provers can generate the next reasoning step correctly with some minimal probability, we show how to learn a strong prover with small error and abstention rates.

Algorithm Design and Stronger Guarantees for the Improving Multi-Armed Bandits Problem

The improving multi-armed bandits problem is a formal model for allocating effort under uncertainty, motivated by scenarios such as investing research effort into new technologies, performing clinical trials, and hyperparameter selection from learning curves. Each pull of an arm provides reward that increases monotonically with diminishing returns. A growing line of work has designed algorithms for improving bandits, albeit with somewhat pessimistic worst-case guarantees. Indeed, strong lower bounds of $Ω(k)$ and $Ω(\sqrt{k})$ multiplicative approximation factors are known for both deterministic and randomized algorithms (respectively) relative to the optimal arm, where $k$ is the number of bandit arms. In this work, we propose two new parameterized families of bandit algorithms and bound the sample complexity of learning the near-optimal algorithm from each family using offline data. The first family we define includes the optimal randomized algorithm from prior work. We show that an appropriately chosen algorithm from this family can achieve stronger guarantees, with optimal dependence on $k$, when the arm reward curves satisfy additional properties related to the strength of concavity. Our second family contains algorithms that both guarantee best-arm identification on well-behaved instances and revert to worst case guarantees on poorly-behaved instances. Taking a statistical learning perspective on the bandit rewards optimization problem, we achieve stronger data-dependent guarantees without the need for actually verifying whether the assumptions are satisfied.

Strategic Filtering for Content Moderation: Free Speech or Free of Distortion?

User-generated content (UGC) on social media platforms is vulnerable to incitements and manipulations, necessitating effective regulations. To address these challenges, those platforms often deploy automated content moderators tasked with evaluating the harmfulness of UGC and filtering out content that violates established guidelines. However, such moderation inevitably gives rise to strategic responses from users, who strive to express themselves within the confines of guidelines. Such phenomena call for a careful balance between: 1. ensuring freedom of speech -- by minimizing the restriction of expression; and 2. reducing social distortion -- measured by the total amount of content manipulation. We tackle the problem of optimizing this balance through the lens of mechanism design, aiming at optimizing the trade-off between minimizing social distortion and maximizing free speech. Although determining the optimal trade-off is NP-hard, we propose practical methods to approximate the optimal solution. Additionally, we provide generalization guarantees determining the amount of finite offline data required to approximate the optimal moderator effectively.

On Learning Verifiers for Chain-of-Thought Reasoning

Chain-of-Thought reasoning has emerged as a powerful approach for solving complex mathematical and logical problems. However, it can often veer off track through incorrect or unsubstantiated inferences. Formal mathematical reasoning, which can be checked with a formal verifier, is one approach to addressing this issue. However, currently LLMs are simply not good enough to solve complex problems in a formal way, and even just formalizing an informal problem statement can be challenging. Motivated by this fact, in this work we consider the problem of learning reliable verifiers for natural language Chain-of-Thought reasoning. That is, given a problem statement and step-by-step solution in natural language, the aim of the verifier is to output [Yes] if the reasoning steps in the solution are all valid, and [No] otherwise. In this work we give a formal PAC-learning framework for studying this problem. We propose and analyze several natural verification goals, at different levels of strength, in this framework. We provide sample complexity upper-bounds for learning verifiers satisfying these goals, as well as lower-bound and impossibility results for learning other natural verification objectives without additional assumptions.

Proofs as Explanations: Short Certificates for Reliable Predictions

We consider a model for explainable AI in which an explanation for a prediction $h(x)=y$ consists of a subset $S'$ of the training data (if it exists) such that all classifiers $h' \in H$ that make at most $b$ mistakes on $S'$ predict $h'(x)=y$. Such a set $S'$ serves as a proof that $x$ indeed has label $y$ under the assumption that (1) the target function $h^\star$ belongs to $H$, and (2) the set $S$ contains at most $b$ corrupted points. For example, if $b=0$ and $H$ is the family of linear classifiers in $\mathbb{R}^d$, and if $x$ lies inside the convex hull of the positive data points in $S$ (and hence every consistent linear classifier labels $x$ as positive), then Carath\'eodory's theorem states that $x$ lies inside the convex hull of $d+1$ of those points. So, a set $S'$ of size $d+1$ could be released as an explanation for a positive prediction, and would serve as a short proof of correctness of the prediction under the assumption of realizability. In this work, we consider this problem more generally, for general hypothesis classes $H$ and general values $b\geq 0$. We define the notion of the robust hollow star number of $H$ (which generalizes the standard hollow star number), and show that it precisely characterizes the worst-case size of the smallest certificate achievable, and analyze its size for natural classes. We also consider worst-case distributional bounds on certificate size, as well as distribution-dependent bounds that we show tightly control the sample size needed to get a certificate for any given test example. In particular, we define a notion of the certificate coefficient $\varepsilon_x$ of an example $x$ with respect to a data distribution $D$ and target function $h^\star$, and prove matching upper and lower bounds on sample size as a function of $\varepsilon_x$, $b$, and the VC dimension $d$ of $H$.

PAC Learning with Improvements

One of the most basic lower bounds in machine learning is that in nearly any nontrivial setting, it takes $\textit{at least}$ $1/\epsilon$ samples to learn to error $\epsilon$ (and more, if the classifier being learned is complex). However, suppose that data points are agents who have the ability to improve by a small amount if doing so will allow them to receive a (desired) positive classification. In that case, we may actually be able to achieve $\textit{zero}$ error by just being "close enough". For example, imagine a hiring test used to measure an agent's skill at some job such that for some threshold $\theta$, agents who score above $\theta$ will be successful and those who score below $\theta$ will not (i.e., learning a threshold on the line). Suppose also that by putting in effort, agents can improve their skill level by some small amount $r$. In that case, if we learn an approximation $\hat{\theta}$ of $\theta$ such that $\theta \leq \hat{\theta} \leq \theta + r$ and use it for hiring, we can actually achieve error zero, in the sense that (a) any agent classified as positive is truly qualified, and (b) any agent who truly is qualified can be classified as positive by putting in effort. Thus, the ability for agents to improve has the potential to allow for a goal one could not hope to achieve in standard models, namely zero error. In this paper, we explore this phenomenon more broadly, giving general results and examining under what conditions the ability of agents to improve can allow for a reduction in the sample complexity of learning, or alternatively, can make learning harder. We also examine both theoretically and empirically what kinds of improvement-aware algorithms can take into account agents who have the ability to improve to a limited extent when it is in their interest to do so.

Replicable Online Learning

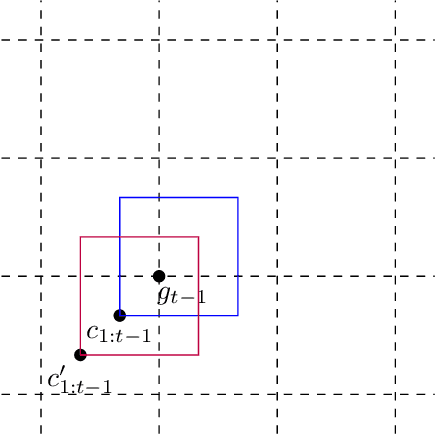
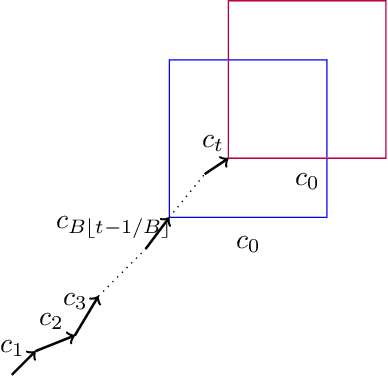
We investigate the concept of algorithmic replicability introduced by Impagliazzo et al. 2022, Ghazi et al. 2021, Ahn et al. 2024 in an online setting. In our model, the input sequence received by the online learner is generated from time-varying distributions chosen by an adversary (obliviously). Our objective is to design low-regret online algorithms that, with high probability, produce the exact same sequence of actions when run on two independently sampled input sequences generated as described above. We refer to such algorithms as adversarially replicable. Previous works (such as Esfandiari et al. 2022) explored replicability in the online setting under inputs generated independently from a fixed distribution; we term this notion as iid-replicability. Our model generalizes to capture both adversarial and iid input sequences, as well as their mixtures, which can be modeled by setting certain distributions as point-masses. We demonstrate adversarially replicable online learning algorithms for online linear optimization and the experts problem that achieve sub-linear regret. Additionally, we propose a general framework for converting an online learner into an adversarially replicable one within our setting, bounding the new regret in terms of the original algorithm's regret. We also present a nearly optimal (in terms of regret) iid-replicable online algorithm for the experts problem, highlighting the distinction between the iid and adversarial notions of replicability. Finally, we establish lower bounds on the regret (in terms of the replicability parameter and time) that any replicable online algorithm must incur.

Regularized Robustly Reliable Learners and Instance Targeted Attacks

Instance-targeted data poisoning attacks, where an adversary corrupts a training set to induce errors on specific test points, have raised significant concerns. Balcan et al (2022) proposed an approach to addressing this challenge by defining a notion of robustly-reliable learners that provide per-instance guarantees of correctness under well-defined assumptions, even in the presence of data poisoning attacks. They then give a generic optimal (but computationally inefficient) robustly reliable learner as well as a computationally efficient algorithm for the case of linear separators over log-concave distributions. In this work, we address two challenges left open by Balcan et al (2022). The first is that the definition of robustly-reliable learners in Balcan et al (2022) becomes vacuous for highly-flexible hypothesis classes: if there are two classifiers h_0, h_1 \in H both with zero error on the training set such that h_0(x) \neq h_1(x), then a robustly-reliable learner must abstain on x. We address this problem by defining a modified notion of regularized robustly-reliable learners that allows for nontrivial statements in this case. The second is that the generic algorithm of Balcan et al (2022) requires re-running an ERM oracle (essentially, retraining the classifier) on each test point x, which is generally impractical even if ERM can be implemented efficiently. To tackle this problem, we show that at least in certain interesting cases we can design algorithms that can produce their outputs in time sublinear in training time, by using techniques from dynamic algorithm design.

A Model for Combinatorial Dictionary Learning and Inference

We are often interested in decomposing complex, structured data into simple components that explain the data. The linear version of this problem is well-studied as dictionary learning and factor analysis. In this work, we propose a combinatorial model in which to study this question, motivated by the way objects occlude each other in a scene to form an image. First, we identify a property we call "well-structuredness" of a set of low-dimensional components which ensures that no two components in the set are too similar. We show how well-structuredness is sufficient for learning the set of latent components comprising a set of sample instances. We then consider the problem: given a set of components and an instance generated from some unknown subset of them, identify which parts of the instance arise from which components. We consider two variants: (1) determine the minimal number of components required to explain the instance; (2) determine the correct explanation for as many locations as possible. For the latter goal, we also devise a version that is robust to adversarial corruptions, with just a slightly stronger assumption on the components. Finally, we show that the learning problem is computationally infeasible in the absence of any assumptions.