DORO: Distributional and Outlier Robust Optimization
Paper and Code
Jun 11, 2021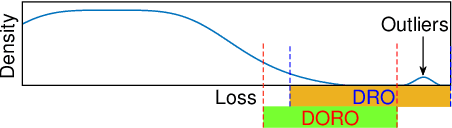
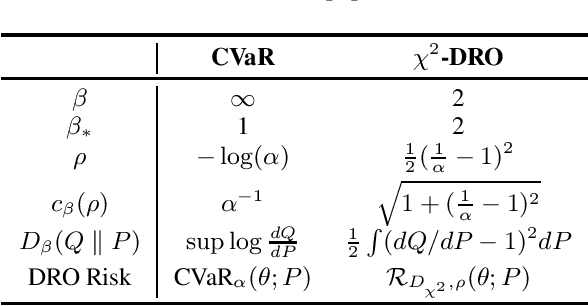
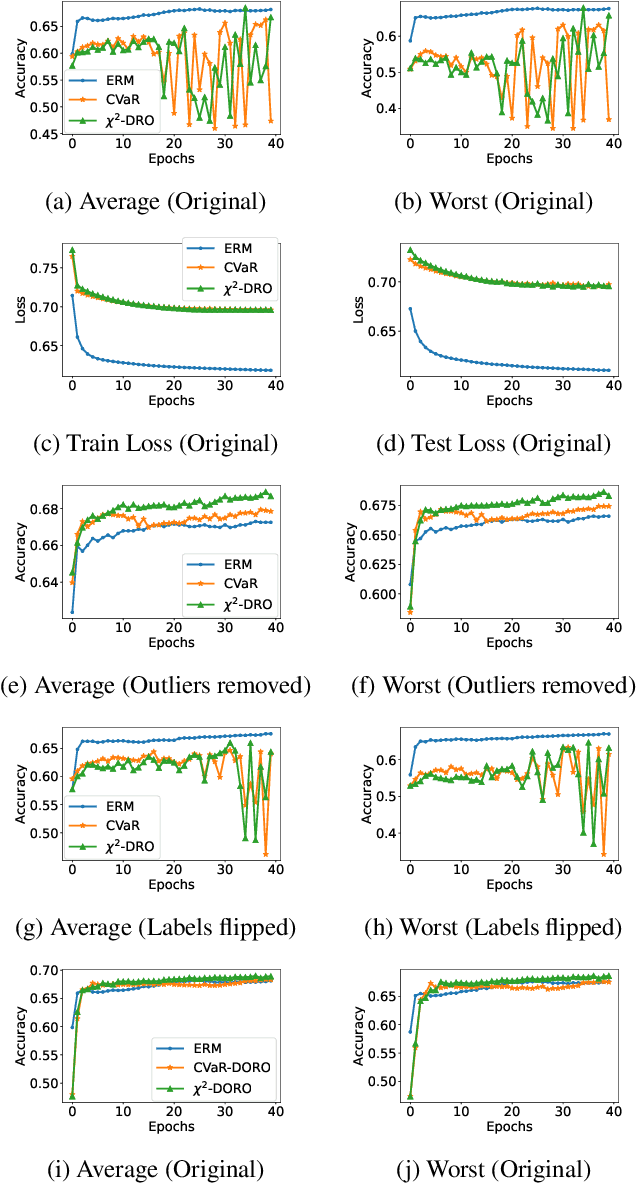
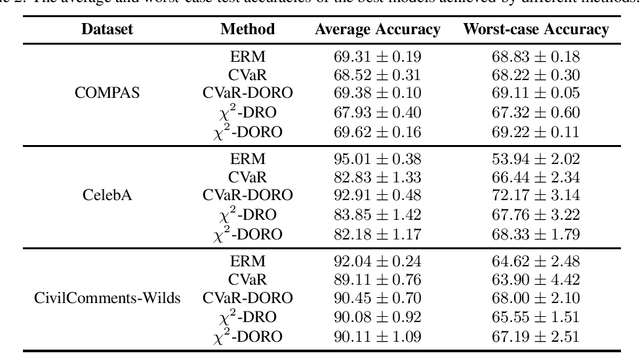
Many machine learning tasks involve subpopulation shift where the testing data distribution is a subpopulation of the training distribution. For such settings, a line of recent work has proposed the use of a variant of empirical risk minimization(ERM) known as distributionally robust optimization (DRO). In this work, we apply DRO to real, large-scale tasks with subpopulation shift, and observe that DRO performs relatively poorly, and moreover has severe instability. We identify one direct cause of this phenomenon: sensitivity of DRO to outliers in the datasets. To resolve this issue, we propose the framework of DORO, for Distributional and Outlier Robust Optimization. At the core of this approach is a refined risk function which prevents DRO from overfitting to potential outliers. We instantiate DORO for the Cressie-Read family of R\'enyi divergence, and delve into two specific instances of this family: CVaR and $\chi^2$-DRO. We theoretically prove the effectiveness of the proposed method, and empirically show that DORO improves the performance and stability of DRO with experiments on large modern datasets, thereby positively addressing the open question raised by Hashimoto et al., 2018.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge