Yuting Wei
Transformers Meet In-Context Learning: A Universal Approximation Theory
Jun 05, 2025Abstract:Modern large language models are capable of in-context learning, the ability to perform new tasks at inference time using only a handful of input-output examples in the prompt, without any fine-tuning or parameter updates. We develop a universal approximation theory to better understand how transformers enable in-context learning. For any class of functions (each representing a distinct task), we demonstrate how to construct a transformer that, without any further weight updates, can perform reliable prediction given only a few in-context examples. In contrast to much of the recent literature that frames transformers as algorithm approximators -- i.e., constructing transformers to emulate the iterations of optimization algorithms as a means to approximate solutions of learning problems -- our work adopts a fundamentally different approach rooted in universal function approximation. This alternative approach offers approximation guarantees that are not constrained by the effectiveness of the optimization algorithms being approximated, thereby extending far beyond convex problems and linear function classes. Our construction sheds light on how transformers can simultaneously learn general-purpose representations and adapt dynamically to in-context examples.
Actor-Critics Can Achieve Optimal Sample Efficiency
May 06, 2025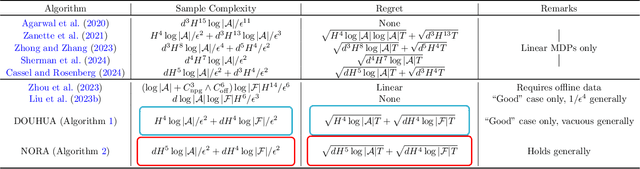
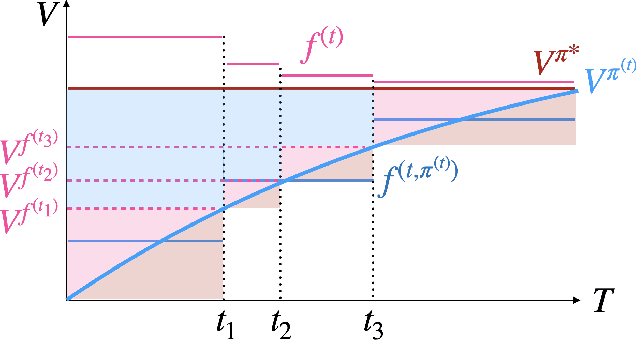
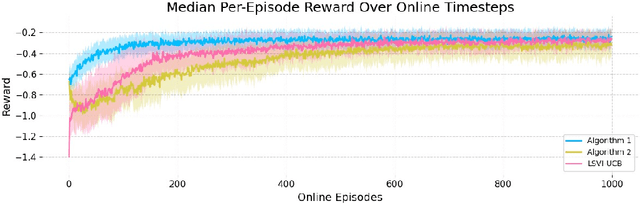
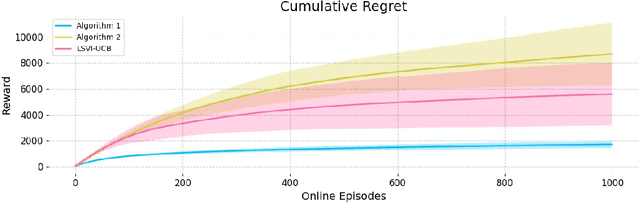
Abstract:Actor-critic algorithms have become a cornerstone in reinforcement learning (RL), leveraging the strengths of both policy-based and value-based methods. Despite recent progress in understanding their statistical efficiency, no existing work has successfully learned an $\epsilon$-optimal policy with a sample complexity of $O(1/\epsilon^2)$ trajectories with general function approximation when strategic exploration is necessary. We address this open problem by introducing a novel actor-critic algorithm that attains a sample-complexity of $O(dH^5 \log|\mathcal{A}|/\epsilon^2 + d H^4 \log|\mathcal{F}|/ \epsilon^2)$ trajectories, and accompanying $\sqrt{T}$ regret when the Bellman eluder dimension $d$ does not increase with $T$ at more than a $\log T$ rate. Here, $\mathcal{F}$ is the critic function class, $\mathcal{A}$ is the action space, and $H$ is the horizon in the finite horizon MDP setting. Our algorithm integrates optimism, off-policy critic estimation targeting the optimal Q-function, and rare-switching policy resets. We extend this to the setting of Hybrid RL, showing that initializing the critic with offline data yields sample efficiency gains compared to purely offline or online RL. Further, utilizing access to offline data, we provide a \textit{non-optimistic} provably efficient actor-critic algorithm that only additionally requires $N_{\text{off}} \geq c_{\text{off}}^*dH^4/\epsilon^2$ in exchange for omitting optimism, where $c_{\text{off}}^*$ is the single-policy concentrability coefficient and $N_{\text{off}}$ is the number of offline samples. This addresses another open problem in the literature. We further provide numerical experiments to support our theoretical findings.
Dimension-Free Convergence of Diffusion Models for Approximate Gaussian Mixtures
Apr 07, 2025Abstract:Diffusion models are distinguished by their exceptional generative performance, particularly in producing high-quality samples through iterative denoising. While current theory suggests that the number of denoising steps required for accurate sample generation should scale linearly with data dimension, this does not reflect the practical efficiency of widely used algorithms like Denoising Diffusion Probabilistic Models (DDPMs). This paper investigates the effectiveness of diffusion models in sampling from complex high-dimensional distributions that can be well-approximated by Gaussian Mixture Models (GMMs). For these distributions, our main result shows that DDPM takes at most $\widetilde{O}(1/\varepsilon)$ iterations to attain an $\varepsilon$-accurate distribution in total variation (TV) distance, independent of both the ambient dimension $d$ and the number of components $K$, up to logarithmic factors. Furthermore, this result remains robust to score estimation errors. These findings highlight the remarkable effectiveness of diffusion models in high-dimensional settings given the universal approximation capability of GMMs, and provide theoretical insights into their practical success.
Uncertainty quantification for Markov chains with application to temporal difference learning
Feb 19, 2025Abstract:Markov chains are fundamental to statistical machine learning, underpinning key methodologies such as Markov Chain Monte Carlo (MCMC) sampling and temporal difference (TD) learning in reinforcement learning (RL). Given their widespread use, it is crucial to establish rigorous probabilistic guarantees on their convergence, uncertainty, and stability. In this work, we develop novel, high-dimensional concentration inequalities and Berry-Esseen bounds for vector- and matrix-valued functions of Markov chains, addressing key limitations in existing theoretical tools for handling dependent data. We leverage these results to analyze the TD learning algorithm, a widely used method for policy evaluation in RL. Our analysis yields a sharp high-probability consistency guarantee that matches the asymptotic variance up to logarithmic factors. Furthermore, we establish a $O(T^{-\frac{1}{4}}\log T)$ distributional convergence rate for the Gaussian approximation of the TD estimator, measured in convex distance. These findings provide new insights into statistical inference for RL algorithms, bridging the gaps between classical stochastic approximation theory and modern reinforcement learning applications.
Denoising diffusion probabilistic models are optimally adaptive to unknown low dimensionality
Oct 24, 2024Abstract:The denoising diffusion probabilistic model (DDPM) has emerged as a mainstream generative model in generative AI. While sharp convergence guarantees have been established for the DDPM, the iteration complexity is, in general, proportional to the ambient data dimension, resulting in overly conservative theory that fails to explain its practical efficiency. This has motivated the recent work Li and Yan (2024a) to investigate how the DDPM can achieve sampling speed-ups through automatic exploitation of intrinsic low dimensionality of data. We strengthen this prior work by demonstrating, in some sense, optimal adaptivity to unknown low dimensionality. For a broad class of data distributions with intrinsic dimension $k$, we prove that the iteration complexity of the DDPM scales nearly linearly with $k$, which is optimal when using KL divergence to measure distributional discrepancy. Our theory is established based on a key observation: the DDPM update rule is equivalent to running a suitably parameterized SDE upon discretization, where the nonlinear component of the drift term is intrinsically low-dimensional.
Statistical Inference for Temporal Difference Learning with Linear Function Approximation
Oct 21, 2024Abstract:Statistical inference with finite-sample validity for the value function of a given policy in Markov decision processes (MDPs) is crucial for ensuring the reliability of reinforcement learning. Temporal Difference (TD) learning, arguably the most widely used algorithm for policy evaluation, serves as a natural framework for this purpose.In this paper, we study the consistency properties of TD learning with Polyak-Ruppert averaging and linear function approximation, and obtain three significant improvements over existing results. First, we derive a novel sharp high-dimensional probability convergence guarantee that depends explicitly on the asymptotic variance and holds under weak conditions. We further establish refined high-dimensional Berry-Esseen bounds over the class of convex sets that guarantee faster rates than those in the literature. Finally, we propose a plug-in estimator for the asymptotic covariance matrix, designed for efficient online computation. These results enable the construction of confidence regions and simultaneous confidence intervals for the linear parameters of the value function, with guaranteed finite-sample coverage. We demonstrate the applicability of our theoretical findings through numerical experiments.
Stochastic Runge-Kutta Methods: Provable Acceleration of Diffusion Models
Oct 07, 2024Abstract:Diffusion models play a pivotal role in contemporary generative modeling, claiming state-of-the-art performance across various domains. Despite their superior sample quality, mainstream diffusion-based stochastic samplers like DDPM often require a large number of score function evaluations, incurring considerably higher computational cost compared to single-step generators like generative adversarial networks. While several acceleration methods have been proposed in practice, the theoretical foundations for accelerating diffusion models remain underexplored. In this paper, we propose and analyze a training-free acceleration algorithm for SDE-style diffusion samplers, based on the stochastic Runge-Kutta method. The proposed sampler provably attains $\varepsilon^2$ error -- measured in KL divergence -- using $\widetilde O(d^{3/2} / \varepsilon)$ score function evaluations (for sufficiently small $\varepsilon$), strengthening the state-of-the-art guarantees $\widetilde O(d^{3} / \varepsilon)$ in terms of dimensional dependency. Numerical experiments validate the efficiency of the proposed method.
Hybrid Reinforcement Learning Breaks Sample Size Barriers in Linear MDPs
Aug 08, 2024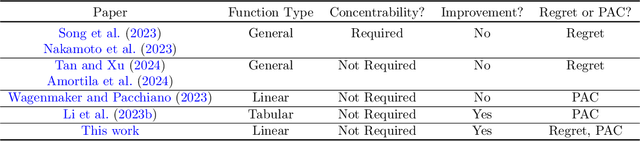
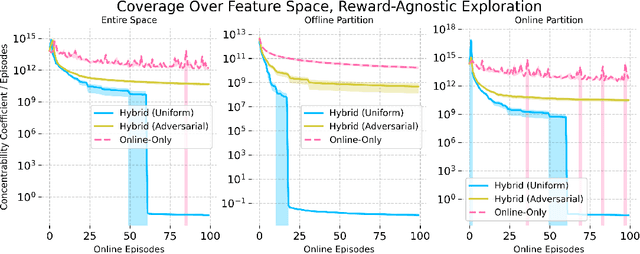

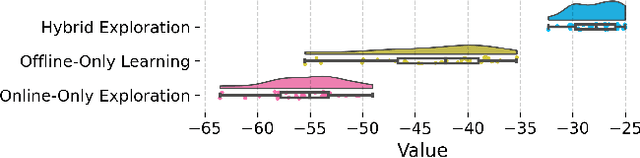
Abstract:Hybrid Reinforcement Learning (RL), where an agent learns from both an offline dataset and online explorations in an unknown environment, has garnered significant recent interest. A crucial question posed by Xie et al. (2022) is whether hybrid RL can improve upon the existing lower bounds established in purely offline and purely online RL without relying on the single-policy concentrability assumption. While Li et al. (2023) provided an affirmative answer to this question in the tabular PAC RL case, the question remains unsettled for both the regret-minimizing RL case and the non-tabular case. In this work, building upon recent advancements in offline RL and reward-agnostic exploration, we develop computationally efficient algorithms for both PAC and regret-minimizing RL with linear function approximation, without single-policy concentrability. We demonstrate that these algorithms achieve sharper error or regret bounds that are no worse than, and can improve on, the optimal sample complexity in offline RL (the first algorithm, for PAC RL) and online RL (the second algorithm, for regret-minimizing RL) in linear Markov decision processes (MDPs), regardless of the quality of the behavior policy. To our knowledge, this work establishes the tightest theoretical guarantees currently available for hybrid RL in linear MDPs.
A Sharp Convergence Theory for The Probability Flow ODEs of Diffusion Models
Aug 05, 2024Abstract:Diffusion models, which convert noise into new data instances by learning to reverse a diffusion process, have become a cornerstone in contemporary generative modeling. In this work, we develop non-asymptotic convergence theory for a popular diffusion-based sampler (i.e., the probability flow ODE sampler) in discrete time, assuming access to $\ell_2$-accurate estimates of the (Stein) score functions. For distributions in $\mathbb{R}^d$, we prove that $d/\varepsilon$ iterations -- modulo some logarithmic and lower-order terms -- are sufficient to approximate the target distribution to within $\varepsilon$ total-variation distance. This is the first result establishing nearly linear dimension-dependency (in $d$) for the probability flow ODE sampler. Imposing only minimal assumptions on the target data distribution (e.g., no smoothness assumption is imposed), our results also characterize how $\ell_2$ score estimation errors affect the quality of the data generation processes. In contrast to prior works, our theory is developed based on an elementary yet versatile non-asymptotic approach without the need of resorting to SDE and ODE toolboxes.
AC-EVAL: Evaluating Ancient Chinese Language Understanding in Large Language Models
Mar 11, 2024


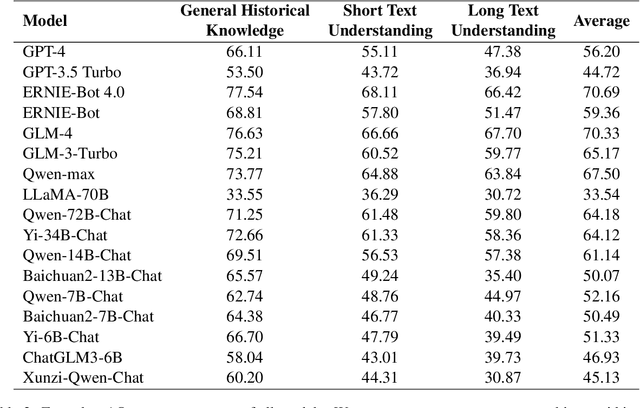
Abstract:Given the importance of ancient Chinese in capturing the essence of rich historical and cultural heritage, the rapid advancements in Large Language Models (LLMs) necessitate benchmarks that can effectively evaluate their understanding of ancient contexts. To meet this need, we present AC-EVAL, an innovative benchmark designed to assess the advanced knowledge and reasoning capabilities of LLMs within the context of ancient Chinese. AC-EVAL is structured across three levels of difficulty reflecting different facets of language comprehension: general historical knowledge, short text understanding, and long text comprehension. The benchmark comprises 13 tasks, spanning historical facts, geography, social customs, art, philosophy, classical poetry and prose, providing a comprehensive assessment framework. Our extensive evaluation of top-performing LLMs, tailored for both English and Chinese, reveals a substantial potential for enhancing ancient text comprehension. By highlighting the strengths and weaknesses of LLMs, AC-EVAL aims to promote their development and application forward in the realms of ancient Chinese language education and scholarly research. The AC-EVAL data and evaluation code are available at https://github.com/yuting-wei/AC-EVAL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge