Preconditioning Benefits of Spectral Orthogonalization in Muon

The Muon optimizer, a matrix-structured algorithm that leverages spectral orthogonalization of gradients, is a milestone in the pretraining of large language models. However, the underlying mechanisms of Muon -- particularly the role of gradient orthogonalization -- remain poorly understood, with very few works providing end-to-end analyses that rigorously explain its advantages in concrete applications. We take a step by studying the effectiveness of a simplified variant of Muon through two case studies: matrix factorization, and in-context learning of linear transformers. For both problems, we prove that simplified Muon converges linearly with iteration complexities independent of the relevant condition number, provably outperforming gradient descent and Adam. Our analysis reveals that the Muon dynamics decouple into a collection of independent scalar sequences in the spectral domain, each exhibiting similar convergence behavior. Our theory formalizes the preconditioning effect induced by spectral orthogonalization, offering insight into Muon's effectiveness in these matrix optimization problems and potentially beyond.

Sample Complexity of Average-Reward Q-Learning: From Single-agent to Federated Reinforcement Learning

Average-reward reinforcement learning offers a principled framework for long-term decision-making by maximizing the mean reward per time step. Although Q-learning is a widely used model-free algorithm with established sample complexity in discounted and finite-horizon Markov decision processes (MDPs), its theoretical guarantees for average-reward settings remain limited. This work studies a simple but effective Q-learning algorithm for average-reward MDPs with finite state and action spaces under the weakly communicating assumption, covering both single-agent and federated scenarios. For the single-agent case, we show that Q-learning with carefully chosen parameters achieves sample complexity $\widetilde{O}\left(\frac{|\mathcal{S}||\mathcal{A}|\|h^{\star}\|_{\mathsf{sp}}^3}{\varepsilon^3}\right)$, where $\|h^{\star}\|_{\mathsf{sp}}$ is the span norm of the bias function, improving previous results by at least a factor of $\frac{\|h^{\star}\|_{\mathsf{sp}}^2}{\varepsilon^2}$. In the federated setting with $M$ agents, we prove that collaboration reduces the per-agent sample complexity to $\widetilde{O}\left(\frac{|\mathcal{S}||\mathcal{A}|\|h^{\star}\|_{\mathsf{sp}}^3}{M\varepsilon^3}\right)$, with only $\widetilde{O}\left(\frac{\|h^{\star}\|_{\mathsf{sp}}}{\varepsilon}\right)$ communication rounds required. These results establish the first federated Q-learning algorithm for average-reward MDPs, with provable efficiency in both sample and communication complexity.

Polynomial Convergence of Riemannian Diffusion Models

Diffusion models have demonstrated remarkable empirical success in the recent years and are considered one of the state-of-the-art generative models in modern AI. These models consist of a forward process, which gradually diffuses the data distribution to a noise distribution spanning the whole space, and a backward process, which inverts this transformation to recover the data distribution from noise. Most of the existing literature assumes that the underlying space is Euclidean. However, in many practical applications, the data are constrained to lie on a submanifold of Euclidean space. Addressing this setting, De Bortoli et al. (2022) introduced Riemannian diffusion models and proved that using an exponentially small step size yields a small sampling error in the Wasserstein distance, provided the data distribution is smooth and strictly positive, and the score estimate is $L_\infty$-accurate. In this paper, we greatly strengthen this theory by establishing that, under $L_2$-accurate score estimate, a {\em polynomially small stepsize} suffices to guarantee small sampling error in the total variation distance, without requiring smoothness or positivity of the data distribution. Our analysis only requires mild and standard curvature assumptions on the underlying manifold. The main ingredients in our analysis are Li-Yau estimate for the log-gradient of heat kernel, and Minakshisundaram-Pleijel parametrix expansion of the perturbed heat equation. Our approach opens the door to a sharper analysis of diffusion models on non-Euclidean spaces.

Transformers Provably Learn Chain-of-Thought Reasoning with Length Generalization

The ability to reason lies at the core of artificial intelligence (AI), and challenging problems usually call for deeper and longer reasoning to tackle. A crucial question about AI reasoning is whether models can extrapolate learned reasoning patterns to solve harder tasks with longer chain-of-thought (CoT). In this work, we present a theoretical analysis of transformers learning on synthetic state-tracking tasks with gradient descent. We mathematically prove how the algebraic structure of state-tracking problems governs the degree of extrapolation of the learned CoT. Specifically, our theory characterizes the length generalization of transformers through the mechanism of attention concentration, linking the retrieval robustness of the attention layer to the state-tracking task structure of long-context reasoning. Moreover, for transformers with limited reasoning length, we prove that a recursive self-training scheme can progressively extend the range of solvable problem lengths. To our knowledge, we provide the first optimization guarantee that constant-depth transformers provably learn $\mathsf{NC}^1$-complete problems with CoT, significantly going beyond prior art confined in $\mathsf{TC}^0$, unless the widely held conjecture $\mathsf{TC}^0 \neq \mathsf{NC}^1$ fails. Finally, we present a broad set of experiments supporting our theoretical results, confirming the length generalization behaviors and the mechanism of attention concentration.

Multi-head Transformers Provably Learn Symbolic Multi-step Reasoning via Gradient Descent

Transformers have demonstrated remarkable capabilities in multi-step reasoning tasks. However, understandings of the underlying mechanisms by which they acquire these abilities through training remain limited, particularly from a theoretical standpoint. This work investigates how transformers learn to solve symbolic multi-step reasoning problems through chain-of-thought processes, focusing on path-finding in trees. We analyze two intertwined tasks: a backward reasoning task, where the model outputs a path from a goal node to the root, and a more complex forward reasoning task, where the model implements two-stage reasoning by first identifying the goal-to-root path and then reversing it to produce the root-to-goal path. Our theoretical analysis, grounded in the dynamics of gradient descent, shows that trained one-layer transformers can provably solve both tasks with generalization guarantees to unseen trees. In particular, our multi-phase training dynamics for forward reasoning elucidate how different attention heads learn to specialize and coordinate autonomously to solve the two subtasks in a single autoregressive path. These results provide a mechanistic explanation of how trained transformers can implement sequential algorithmic procedures. Moreover, they offer insights into the emergence of reasoning abilities, suggesting that when tasks are structured to take intermediate chain-of-thought steps, even shallow multi-head transformers can effectively solve problems that would otherwise require deeper architectures.

Scalable LLM Math Reasoning Acceleration with Low-rank Distillation

Due to long generations, large language model (LLM) math reasoning demands significant computational resources and time. While many existing efficient inference methods have been developed with excellent performance preservation on language tasks, they often severely degrade math performance. In this paper, we propose Caprese, a low-cost distillation method to recover lost capabilities from deploying efficient inference methods, focused primarily in feedforward blocks. With original weights unperturbed, roughly 1% of additional parameters, and only 20K synthetic training samples, we are able to recover much if not all of the math capabilities lost from efficient inference for thinking LLMs and without harm to language tasks for instruct LLMs. Moreover, Caprese slashes the number of active parameters (~2B cut for Gemma 2 9B and Llama 3.1 8B) and integrates cleanly into existing model layers to reduce latency (>11% reduction to generate 2048 tokens with Qwen 2.5 14B) while encouraging response brevity.

LoRe: Personalizing LLMs via Low-Rank Reward Modeling

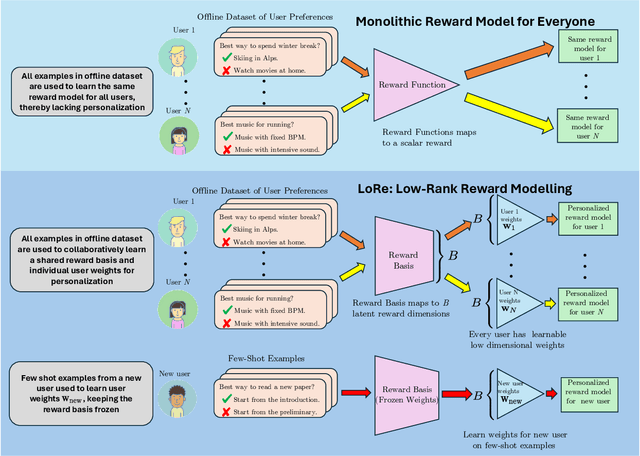
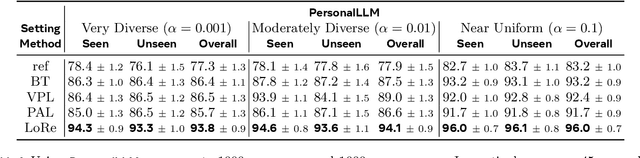
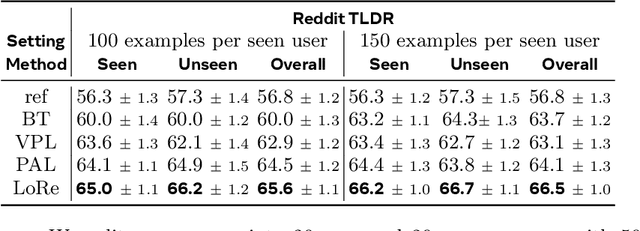
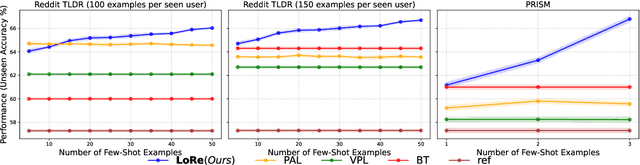
Personalizing large language models (LLMs) to accommodate diverse user preferences is essential for enhancing alignment and user satisfaction. Traditional reinforcement learning from human feedback (RLHF) approaches often rely on monolithic value representations, limiting their ability to adapt to individual preferences. We introduce a novel framework that leverages low-rank preference modeling to efficiently learn and generalize user-specific reward functions. By representing reward functions in a low-dimensional subspace and modeling individual preferences as weighted combinations of shared basis functions, our approach avoids rigid user categorization while enabling scalability and few-shot adaptation. We validate our method on multiple preference datasets, demonstrating superior generalization to unseen users and improved accuracy in preference prediction tasks.

Robust Gymnasium: A Unified Modular Benchmark for Robust Reinforcement Learning

Driven by inherent uncertainty and the sim-to-real gap, robust reinforcement learning (RL) seeks to improve resilience against the complexity and variability in agent-environment sequential interactions. Despite the existence of a large number of RL benchmarks, there is a lack of standardized benchmarks for robust RL. Current robust RL policies often focus on a specific type of uncertainty and are evaluated in distinct, one-off environments. In this work, we introduce Robust-Gymnasium, a unified modular benchmark designed for robust RL that supports a wide variety of disruptions across all key RL components-agents' observed state and reward, agents' actions, and the environment. Offering over sixty diverse task environments spanning control and robotics, safe RL, and multi-agent RL, it provides an open-source and user-friendly tool for the community to assess current methods and foster the development of robust RL algorithms. In addition, we benchmark existing standard and robust RL algorithms within this framework, uncovering significant deficiencies in each and offering new insights.

Characterizing the Accuracy-Communication-Privacy Trade-off in Distributed Stochastic Convex Optimization

We consider the problem of differentially private stochastic convex optimization (DP-SCO) in a distributed setting with $M$ clients, where each of them has a local dataset of $N$ i.i.d. data samples from an underlying data distribution. The objective is to design an algorithm to minimize a convex population loss using a collaborative effort across $M$ clients, while ensuring the privacy of the local datasets. In this work, we investigate the accuracy-communication-privacy trade-off for this problem. We establish matching converse and achievability results using a novel lower bound and a new algorithm for distributed DP-SCO based on Vaidya's plane cutting method. Thus, our results provide a complete characterization of the accuracy-communication-privacy trade-off for DP-SCO in the distributed setting.

Vertical Federated Learning with Missing Features During Training and Inference

Vertical federated learning trains models from feature-partitioned datasets across multiple clients, who collaborate without sharing their local data. Standard approaches assume that all feature partitions are available during both training and inference. Yet, in practice, this assumption rarely holds, as for many samples only a subset of the clients observe their partition. However, not utilizing incomplete samples during training harms generalization, and not supporting them during inference limits the utility of the model. Moreover, if any client leaves the federation after training, its partition becomes unavailable, rendering the learned model unusable. Missing feature blocks are therefore a key challenge limiting the applicability of vertical federated learning in real-world scenarios. To address this, we propose LASER-VFL, a vertical federated learning method for efficient training and inference of split neural network-based models that is capable of handling arbitrary sets of partitions. Our approach is simple yet effective, relying on the strategic sharing of model parameters and on task-sampling to train a family of predictors. We show that LASER-VFL achieves a $\mathcal{O}({1}/{\sqrt{T}})$ convergence rate for nonconvex objectives in general, $\mathcal{O}({1}/{T})$ for sufficiently large batch sizes, and linear convergence under the Polyak-{\L}ojasiewicz inequality. Numerical experiments show improved performance of LASER-VFL over the baselines. Remarkably, this is the case even in the absence of missing features. For example, for CIFAR-100, we see an improvement in accuracy of $21.4\%$ when each of four feature blocks is observed with a probability of 0.5 and of $12.2\%$ when all features are observed.