The Sample-Communication Complexity Trade-off in Federated Q-Learning

We consider the problem of federated Q-learning, where $M$ agents aim to collaboratively learn the optimal Q-function of an unknown infinite-horizon Markov decision process with finite state and action spaces. We investigate the trade-off between sample and communication complexities for the widely used class of intermittent communication algorithms. We first establish the converse result, where it is shown that a federated Q-learning algorithm that offers any speedup with respect to the number of agents in the per-agent sample complexity needs to incur a communication cost of at least an order of $\frac{1}{1-\gamma}$ up to logarithmic factors, where $\gamma$ is the discount factor. We also propose a new algorithm, called Fed-DVR-Q, which is the first federated Q-learning algorithm to simultaneously achieve order-optimal sample and communication complexities. Thus, together these results provide a complete characterization of the sample-communication complexity trade-off in federated Q-learning.

Order-Optimal Regret in Distributed Kernel Bandits using Uniform Sampling with Shared Randomness

We consider distributed kernel bandits where $N$ agents aim to collaboratively maximize an unknown reward function that lies in a reproducing kernel Hilbert space. Each agent sequentially queries the function to obtain noisy observations at the query points. Agents can share information through a central server, with the objective of minimizing regret that is accumulating over time $T$ and aggregating over agents. We develop the first algorithm that achieves the optimal regret order (as defined by centralized learning) with a communication cost that is sublinear in both $N$ and $T$. The key features of the proposed algorithm are the uniform exploration at the local agents and shared randomness with the central server. Working together with the sparse approximation of the GP model, these two key components make it possible to preserve the learning rate of the centralized setting at a diminishing rate of communication.

Random Exploration in Bayesian Optimization: Order-Optimal Regret and Computational Efficiency

We consider Bayesian optimization using Gaussian Process models, also referred to as kernel-based bandit optimization. We study the methodology of exploring the domain using random samples drawn from a distribution. We show that this random exploration approach achieves the optimal error rates. Our analysis is based on novel concentration bounds in an infinite dimensional Hilbert space established in this work, which may be of independent interest. We further develop an algorithm based on random exploration with domain shrinking and establish its order-optimal regret guarantees under both noise-free and noisy settings. In the noise-free setting, our analysis closes the existing gap in regret performance and thereby resolves a COLT open problem. The proposed algorithm also enjoys a computational advantage over prevailing methods due to the random exploration that obviates the expensive optimization of a non-convex acquisition function for choosing the query points at each iteration.

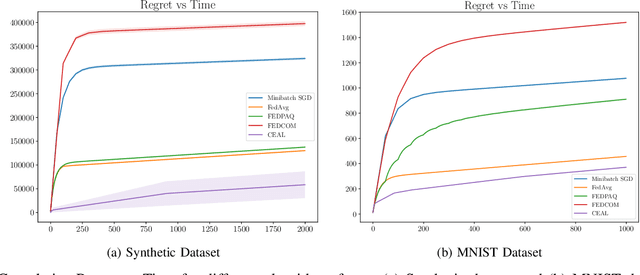
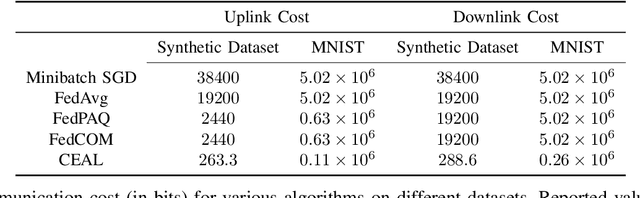
A Communication-Efficient Adaptive Algorithm for Federated Learning under Cumulative Regret

We consider the problem of online stochastic optimization in a distributed setting with $M$ clients connected through a central server. We develop a distributed online learning algorithm that achieves order-optimal cumulative regret with low communication cost measured in the total number of bits transmitted over the entire learning horizon. This is in contrast to existing studies which focus on the offline measure of simple regret for learning efficiency. The holistic measure for communication cost also departs from the prevailing approach that \emph{separately} tackles the communication frequency and the number of bits in each communication round.

Distributed Linear Bandits under Communication Constraints

We consider distributed linear bandits where $M$ agents learn collaboratively to minimize the overall cumulative regret incurred by all agents. Information exchange is facilitated by a central server, and both the uplink and downlink communications are carried over channels with fixed capacity, which limits the amount of information that can be transmitted in each use of the channels. We investigate the regret-communication trade-off by (i) establishing information-theoretic lower bounds on the required communications (in terms of bits) for achieving a sublinear regret order; (ii) developing an efficient algorithm that achieves the minimum sublinear regret order offered by centralized learning using the minimum order of communications dictated by the information-theoretic lower bounds. For sparse linear bandits, we show a variant of the proposed algorithm offers better regret-communication trade-off by leveraging the sparsity of the problem.

Kernel-based Federated Learning with Personalization

We consider federated learning with personalization, where in addition to a global objective, each client is also interested in maximizing a personalized local objective. We consider this problem under a general continuous action space setting where the objective functions belong to a reproducing kernel Hilbert space. We propose algorithms based on surrogate Gaussian process (GP) models that achieve the optimal regret order (up to polylogarithmic factors). Furthermore, we show that the sparse approximations of the GP models significantly reduce the communication cost across clients.

Provably and Practically Efficient Neural Contextual Bandits

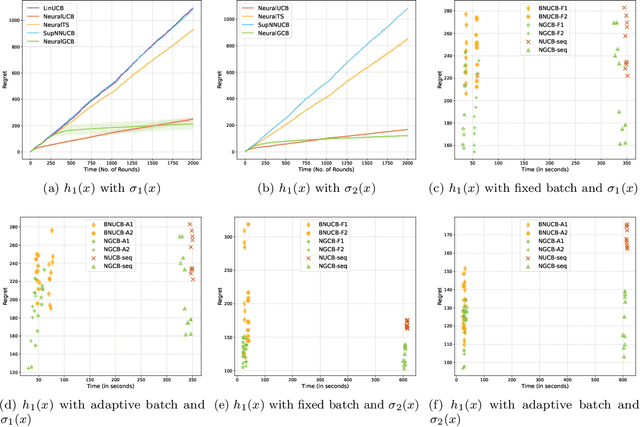
We consider the neural contextual bandit problem. In contrast to the existing work which primarily focuses on ReLU neural nets, we consider a general set of smooth activation functions. Under this more general setting, (i) we derive non-asymptotic error bounds on the difference between an overparameterized neural net and its corresponding neural tangent kernel, (ii) we propose an algorithm with a provably sublinear regret bound that is also efficient in the finite regime as demonstrated by empirical studies. The non-asymptotic error bounds may be of broader interest as a tool to establish the relation between the smoothness of the activation functions in neural contextual bandits and the smoothness of the kernels in kernel bandits.

As Easy as ABC: Adaptive Binning Coincidence Test for Uniformity Testing

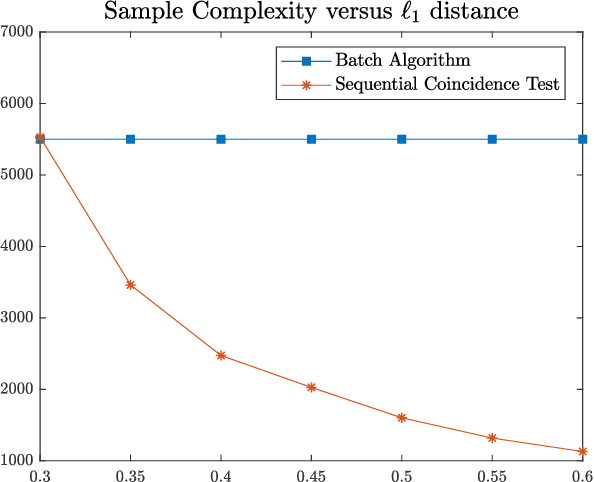
We consider the problem of uniformity testing of Lipschitz continuous distributions with bounded support. The alternative hypothesis is a composite set of Lipschitz continuous distributions that are at least $\varepsilon$ away in $\ell_1$ distance from the uniform distribution. We propose a sequential test that adapts to the unknown distribution under the alternative hypothesis. Referred to as the Adaptive Binning Coincidence (ABC) test, the proposed strategy adapts in two ways. First, it partitions the set of alternative distributions into layers based on their distances to the uniform distribution. It then sequentially eliminates the alternative distributions layer by layer in decreasing distance to the uniform, and subsequently takes advantage of favorable situations of a distant alternative by exiting early. Second, it adapts, across layers of the alternative distributions, the resolution level of the discretization for computing the coincidence statistic. The farther away the layer is from the uniform, the coarser the discretization is needed for eliminating/exiting this layer. It thus exits both early in the detection process and quickly by using a lower resolution to take advantage of favorable alternative distributions. The ABC test builds on a novel sequential coincidence test for discrete distributions, which is of independent interest. We establish the sample complexity of the proposed tests as well as a lower bound.

A Computationally Efficient Approach to Black-box Optimization using Gaussian Process Models

We consider the sequential optimization of an unknown function from noisy feedback using Gaussian process modeling. A prevailing approach to this problem involves choosing query points based on finding the maximum of an upper confidence bound (UCB) score over the entire domain of the function. Due to the multi-modal nature of the UCB, this maximization can only be approximated, usually using an increasingly fine sequence of discretizations of the entire domain, making such methods computationally prohibitive. We propose a general approach that reduces the computational complexity of this class of algorithms by a factor of $O(T^{2d-1})$ (where $T$ is the time horizon and $d$ the dimension of the function domain), while preserving the same regret order. The significant reduction in computational complexity results from two key features of the proposed approach: (i) a tree-based localized search strategy rooted in the methodology of domain shrinking to achieve increasing accuracy with a constant-size discretization; (ii) a localized optimization with the objective relaxed from a global maximizer to any point with value exceeding a given threshold, where the threshold is updated iteratively to approach the maximum as the search deepens. More succinctly, the proposed optimization strategy is a sequence of localized searches in the domain of the function guided by an iterative search in the range of the function to approach the maximum.

Stochastic Coordinate Minimization with Progressive Precision for Stochastic Convex Optimization

A framework based on iterative coordinate minimization (CM) is developed for stochastic convex optimization. Given that exact coordinate minimization is impossible due to the unknown stochastic nature of the objective function, the crux of the proposed optimization algorithm is an optimal control of the minimization precision in each iteration. We establish the optimal precision control and the resulting order-optimal regret performance for strongly convex and separably nonsmooth functions. An interesting finding is that the optimal progression of precision across iterations is independent of the low-dimensional CM routine employed, suggesting a general framework for extending low-dimensional optimization routines to high-dimensional problems. The proposed algorithm is amenable to online implementation and inherits the scalability and parallelizability properties of CM for large-scale optimization. Requiring only a sublinear order of message exchanges, it also lends itself well to distributed computing as compared with the alternative approach of coordinate gradient descent.