Grid Monitoring and Protection with Continuous Point-on-Wave Measurements and Generative AI

Purpose This article presents a case for a next-generation grid monitoring and control system, leveraging recent advances in generative artificial intelligence (AI), machine learning, and statistical inference. Advancing beyond earlier generations of wide-area monitoring systems built upon supervisory control and data acquisition (SCADA) and synchrophasor technologies, we argue for a monitoring and control framework based on the streaming of continuous point-on-wave (CPOW) measurements with AI-powered data compression and fault detection. Methods and Results: The architecture of the proposed design originates from the Wiener-Kallianpur innovation representation of a random process that transforms causally a stationary random process into an innovation sequence with independent and identically distributed random variables. This work presents a generative AI approach that (i) learns an innovation autoencoder that extracts innovation sequence from CPOW time series, (ii) compresses the CPOW streaming data with innovation autoencoder and subband coding, and (iii) detects unknown faults and novel trends via nonparametric sequential hypothesis testing. Conclusion: This work argues that conventional monitoring using SCADA and phasor measurement unit (PMU) technologies is ill-suited for a future grid with deep penetration of inverter-based renewable generations and distributed energy resources. A monitoring system based on CPOW data streaming and AI data analytics should be the basic building blocks for situational awareness of a highly dynamic future grid.

Generative Probabilistic Forecasting with Applications in Market Operations

This paper presents a novel generative probabilistic forecasting approach derived from the Wiener-Kallianpur innovation representation of nonparametric time series. Under the paradigm of generative artificial intelligence, the proposed forecasting architecture includes an autoencoder that transforms nonparametric multivariate random processes into canonical innovation sequences, from which future time series samples are generated according to their probability distributions conditioned on past samples. A novel deep-learning algorithm is proposed that constrains the latent process to be an independent and identically distributed sequence with matching autoencoder input-output conditional probability distributions. Asymptotic optimality and structural convergence properties of the proposed generative forecasting approach are established. Three applications involving highly dynamic and volatile time series in real-time market operations are considered: (i) locational marginal price forecasting for merchant storage participants, {(ii) interregional price spread forecasting for interchange markets,} and (iii) area control error forecasting for frequency regulations. Numerical studies based on market data from multiple independent system operators demonstrate superior performance against leading traditional and machine learning-based forecasting techniques under both probabilistic and point forecast metrics.

Generative Probabilistic Time Series Forecasting and Applications in Grid Operations

Generative probabilistic forecasting produces future time series samples according to the conditional probability distribution given past time series observations. Such techniques are essential in risk-based decision-making and planning under uncertainty with broad applications in grid operations, including electricity price forecasting, risk-based economic dispatch, and stochastic optimizations. Inspired by Wiener and Kallianpur's innovation representation, we propose a weak innovation autoencoder architecture and a learning algorithm to extract independent and identically distributed innovation sequences from nonparametric stationary time series. We show that the weak innovation sequence is Bayesian sufficient, which makes the proposed weak innovation autoencoder a canonical architecture for generative probabilistic forecasting. The proposed technique is applied to forecasting highly volatile real-time electricity prices, demonstrating superior performance across multiple forecasting measures over leading probabilistic and point forecasting techniques.

Non-parametric Probabilistic Time Series Forecasting via Innovations Representation

Probabilistic time series forecasting predicts the conditional probability distributions of the time series at a future time given past realizations. Such techniques are critical in risk-based decision-making and planning under uncertainties. Existing approaches are primarily based on parametric or semi-parametric time-series models that are restrictive, difficult to validate, and challenging to adapt to varying conditions. This paper proposes a nonparametric method based on the classic notion of {\em innovations} pioneered by Norbert Wiener and Gopinath Kallianpur that causally transforms a nonparametric random process to an independent and identical uniformly distributed {\em innovations process}. We present a machine-learning architecture and a learning algorithm that circumvent two limitations of the original Wiener-Kallianpur innovations representation: (i) the need for known probability distributions of the time series and (ii) the existence of a causal decoder that reproduces the original time series from the innovations representation. We develop a deep-learning approach and a Monte Carlo sampling technique to obtain a generative model for the predicted conditional probability distribution of the time series based on a weak notion of Wiener-Kallianpur innovations representation. The efficacy of the proposed probabilistic forecasting technique is demonstrated on a variety of electricity price datasets, showing marked improvement over leading benchmarks of probabilistic forecasting techniques.

Novelty Detection in Time Series via Weak Innovations Representation: A Deep Learning Approach

We consider novelty detection in time series with unknown and nonparametric probability structures. A deep learning approach is proposed to causally extract an innovations sequence consisting of novelty samples statistically independent of all past samples of the time series. A novelty detection algorithm is developed for the online detection of novel changes in the probability structure in the innovations sequence. A minimax optimality under a Bayes risk measure is established for the proposed novelty detection method, and its robustness and efficacy are demonstrated in experiments using real and synthetic datasets.

As Easy as ABC: Adaptive Binning Coincidence Test for Uniformity Testing

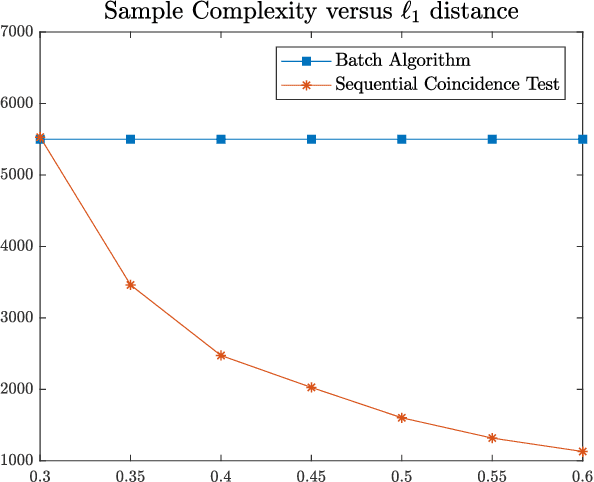
We consider the problem of uniformity testing of Lipschitz continuous distributions with bounded support. The alternative hypothesis is a composite set of Lipschitz continuous distributions that are at least $\varepsilon$ away in $\ell_1$ distance from the uniform distribution. We propose a sequential test that adapts to the unknown distribution under the alternative hypothesis. Referred to as the Adaptive Binning Coincidence (ABC) test, the proposed strategy adapts in two ways. First, it partitions the set of alternative distributions into layers based on their distances to the uniform distribution. It then sequentially eliminates the alternative distributions layer by layer in decreasing distance to the uniform, and subsequently takes advantage of favorable situations of a distant alternative by exiting early. Second, it adapts, across layers of the alternative distributions, the resolution level of the discretization for computing the coincidence statistic. The farther away the layer is from the uniform, the coarser the discretization is needed for eliminating/exiting this layer. It thus exits both early in the detection process and quickly by using a lower resolution to take advantage of favorable alternative distributions. The ABC test builds on a novel sequential coincidence test for discrete distributions, which is of independent interest. We establish the sample complexity of the proposed tests as well as a lower bound.

Innovations Autoencoder and its Application in One-class Anomalous Sequence Detection

An innovations sequence of a time series is a sequence of independent and identically distributed random variables with which the original time series has a causal representation. The innovation at a time is statistically independent of the history of the time series. As such, it represents the new information contained at present but not in the past. Because of its simple probability structure, an innovations sequence is the most efficient signature of the original. Unlike the principle or independent component analysis representations, an innovations sequence preserves not only the complete statistical properties but also the temporal order of the original time series. An long-standing open problem is to find a computationally tractable way to extract an innovations sequence of non-Gaussian processes. This paper presents a deep learning approach, referred to as Innovations Autoencoder (IAE), that extracts innovations sequences using a causal convolutional neural network. An application of IAE to the one-class anomalous sequence detection problem with unknown anomaly and anomaly-free models is also presented.

State and Topology Estimation for Unobservable Distribution Systems using Deep Neural Networks

Time-synchronized state estimation for reconfigurable distribution networks is challenging because of limited real-time observability. This paper addresses this challenge by formulating a deep learning (DL)-based approach for topology identification (TI) and unbalanced three-phase distribution system state estimation (DSSE). Two deep neural networks (DNNs) are trained to operate in a sequential manner for implementing DNN-based TI and DSSE for systems that are incompletely observed by synchrophasor measurement devices (SMDs). A data-driven approach for judicious measurement selection to facilitate reliable TI and DSSE is also provided. Robustness of the proposed methodology is demonstrated by considering realistic measurement error models for SMDs as well as presence of renewable energy. A comparative study of the DNN-based DSSE with classical linear state estimation (LSE) indicates that the DL-based approach gives better accuracy with a significantly smaller number of SMDs

Non-Bayesian Parametric Missing-Mass Estimation

We consider the classical problem of missing-mass estimation, which deals with estimating the total probability of unseen elements in a sample. The missing-mass estimation problem has various applications in machine learning, statistics, language processing, ecology, sensor networks, and others. The naive, constrained maximum likelihood (CML) estimator is inappropriate for this problem since it tends to overestimate the probability of the observed elements. Similarly, the conventional constrained Cramer-Rao bound (CCRB), which is a lower bound on the mean-squared-error (MSE) of unbiased estimators, does not provide a relevant bound on the performance for this problem. In this paper, we introduce a frequentist, non-Bayesian parametric model of the problem of missing-mass estimation. We introduce the concept of missing-mass unbiasedness by using the Lehmann unbiasedness definition. We derive a non-Bayesian CCRB-type lower bound on the missing-mass MSE (mmMSE), named the missing-mass CCRB (mmCCRB), based on the missing-mass unbiasedness. The missing-mass unbiasedness and the proposed mmCCRB can be used to evaluate the performance of existing estimators. Based on the new mmCCRB, we propose a new method to improve existing estimators by an iterative missing-mass Fisher scoring method. Finally, we demonstrate via numerical simulations that the proposed mmCCRB is a valid and informative lower bound on the mmMSE of state-of-the-art estimators for this problem: the CML, the Good-Turing, and Laplace estimators. We also show that the performance of the Laplace estimator is improved by using the new Fisher-scoring method.

Bad-Data Sequence Detection for Power System State Estimation via ICA-GAN

A deep learning approach to the detection of bad-data sequences in power systems is proposed. The bad-data model is nonparametric that includes arbitrary natural and adversarial data anomalies. No historical samples of data anomaly are assumed. The probability distribution of data in anomaly-free system operations is also non-parametric, unknown, but with historical training samples. A uniformity test is proposed based on a generative adversarial network (GAN) that extracts independent components of the measurement sequence via independent component analysis (ICA). Referred to as ICA-GAN, the developed approach to bad-data sequence detection can be applied at the individual sensor level or jointly at the system level. Numerical results demonstrate significant improvement over the state-of-the-art solutions for a variety of bad-data cases using PMU measurements from the EPFL smart grid testbed and that from the synthetic Northern Texas grid.