Learning Networks from Wide-Sense Stationary Stochastic Processes

Complex networked systems driven by latent inputs are common in fields like neuroscience, finance, and engineering. A key inference problem here is to learn edge connectivity from node outputs (potentials). We focus on systems governed by steady-state linear conservation laws: $X_t = {L^{\ast}}Y_{t}$, where $X_t, Y_t \in \mathbb{R}^p$ denote inputs and potentials, respectively, and the sparsity pattern of the $p \times p$ Laplacian $L^{\ast}$ encodes the edge structure. Assuming $X_t$ to be a wide-sense stationary stochastic process with a known spectral density matrix, we learn the support of $L^{\ast}$ from temporally correlated samples of $Y_t$ via an $\ell_1$-regularized Whittle's maximum likelihood estimator (MLE). The regularization is particularly useful for learning large-scale networks in the high-dimensional setting where the network size $p$ significantly exceeds the number of samples $n$. We show that the MLE problem is strictly convex, admitting a unique solution. Under a novel mutual incoherence condition and certain sufficient conditions on $(n, p, d)$, we show that the ML estimate recovers the sparsity pattern of $L^\ast$ with high probability, where $d$ is the maximum degree of the graph underlying $L^{\ast}$. We provide recovery guarantees for $L^\ast$ in element-wise maximum, Frobenius, and operator norms. Finally, we complement our theoretical results with several simulation studies on synthetic and benchmark datasets, including engineered systems (power and water networks), and real-world datasets from neural systems (such as the human brain).

Unraveling overoptimism and publication bias in ML-driven science

Machine Learning (ML) is increasingly used across many disciplines with impressive reported results across many domain areas. However, recent studies suggest that the published performance of ML models are often overoptimistic and not reflective of true accuracy were these models to be deployed. Validity concerns are underscored by findings of a concerning inverse relationship between sample size and reported accuracy in published ML models across several domains. This is in contrast with the theory of learning curves in ML, where we expect accuracy to improve or stay the same with increasing sample size. This paper investigates the factors contributing to overoptimistic accuracy reports in ML-based science, focusing on data leakage and publication bias. Our study introduces a novel stochastic model for observed accuracy, integrating parametric learning curves and the above biases. We then construct an estimator based on this model that corrects for these biases in observed data. Theoretical and empirical results demonstrate that this framework can estimate the underlying learning curve that gives rise to the observed overoptimistic results, thereby providing more realistic performance assessments of ML performance from a collection of published results. We apply the model to various meta-analyses in the digital health literature, including neuroimaging-based and speech-based classifications of several neurological conditions. Our results indicate prevalent overoptimism across these fields and we estimate the inherent limits of ML-based prediction in each domain.

Active Sequential Two-Sample Testing

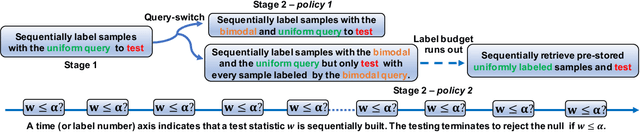
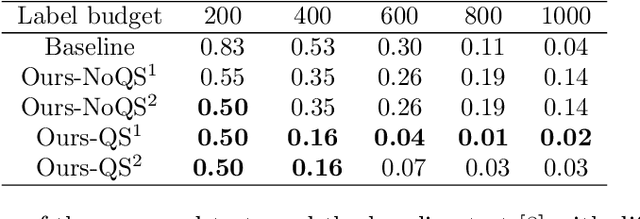
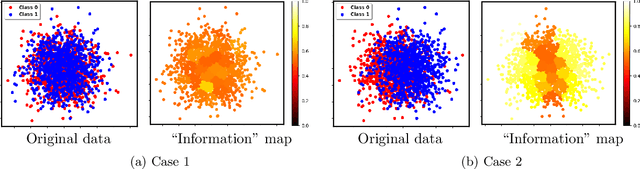
Two-sample testing tests whether the distributions generating two samples are identical. We pose the two-sample testing problem in a new scenario where the sample measurements (or sample features) are inexpensive to access, but their group memberships (or labels) are costly. We devise the first \emph{active sequential two-sample testing framework} that not only sequentially but also \emph{actively queries} sample labels to address the problem. Our test statistic is a likelihood ratio where one likelihood is found by maximization over all class priors, and the other is given by a classification model. The classification model is adaptively updated and then used to guide an active query scheme called bimodal query to label sample features in the regions with high dependency between the feature variables and the label variables. The theoretical contributions in the paper include proof that our framework produces an \emph{anytime-valid} $p$-value; and, under reachable conditions and a mild assumption, the framework asymptotically generates a minimum normalized log-likelihood ratio statistic that a passive query scheme can only achieve when the feature variable and the label variable have the highest dependence. Lastly, we provide a \emph{query-switching (QS)} algorithm to decide when to switch from passive query to active query and adapt bimodal query to increase the testing power of our test. Extensive experiments justify our theoretical contributions and the effectiveness of QS.

Robust Model Selection of Non Tree-Structured Gaussian Graphical Models

We consider the problem of learning the structure underlying a Gaussian graphical model when the variables (or subsets thereof) are corrupted by independent noise. A recent line of work establishes that even for tree-structured graphical models, only partial structure recovery is possible and goes on to devise algorithms to identify the structure up to an (unavoidable) equivalence class of trees. We extend these results beyond trees and consider the model selection problem under noise for non tree-structured graphs, as tree graphs cannot model several real-world scenarios. Although unidentifiable, we show that, like the tree-structured graphs, the ambiguity is limited to an equivalence class. This limited ambiguity can help provide meaningful clustering information (even with noise), which is helpful in computer and social networks, protein-protein interaction networks, and power networks. Furthermore, we devise an algorithm based on a novel ancestral testing method for recovering the equivalence class. We complement these results with finite sample guarantees for the algorithm in the high-dimensional regime.

Transmission Line Parameter Estimation Under Non-Gaussian Measurement Noise

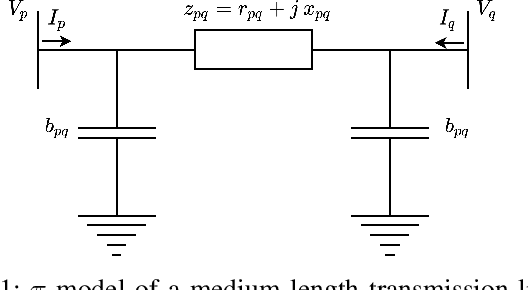
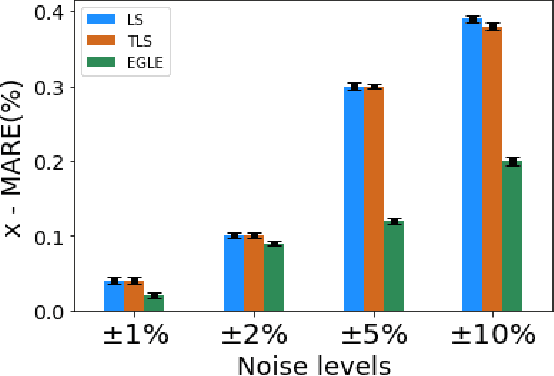
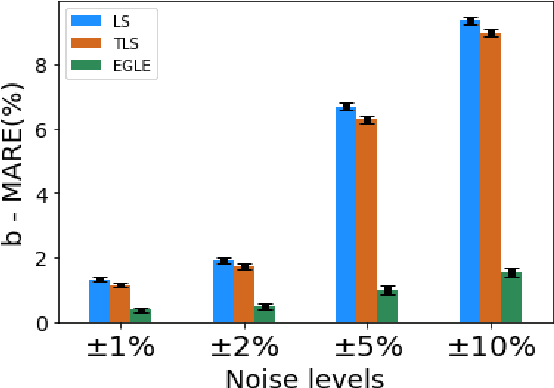
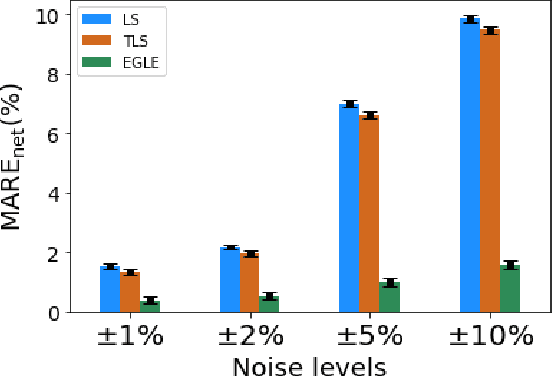
Accurate knowledge of transmission line parameters is essential for a variety of power system monitoring, protection, and control applications. The use of phasor measurement unit (PMU) data for transmission line parameter estimation (TLPE) is well-documented. However, existing literature on PMU-based TLPE implicitly assumes the measurement noise to be Gaussian. Recently, it has been shown that the noise in PMU measurements (especially in the current phasors) is better represented by Gaussian mixture models (GMMs), i.e., the noises are non-Gaussian. We present a novel approach for TLPE that can handle non-Gaussian noise in the PMU measurements. The measurement noise is expressed as a GMM, whose components are identified using the expectation-maximization (EM) algorithm. Subsequently, noise and parameter estimation is carried out by solving a maximum likelihood estimation problem iteratively until convergence. The superior performance of the proposed approach over traditional approaches such as least squares and total least squares as well as the more recently proposed minimum total error entropy approach is demonstrated by performing simulations using the IEEE 118-bus system as well as proprietary PMU data obtained from a U.S. power utility.

Controllability of Coarsely Measured Networked Linear Dynamical Systems (Extended Version)

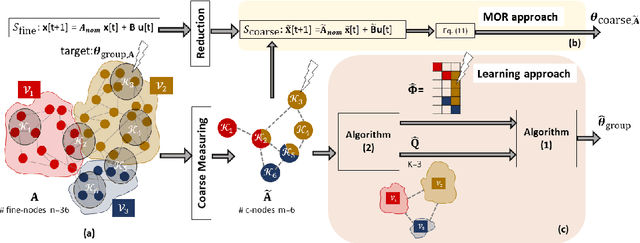
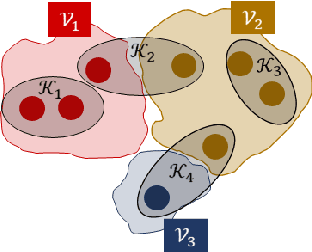
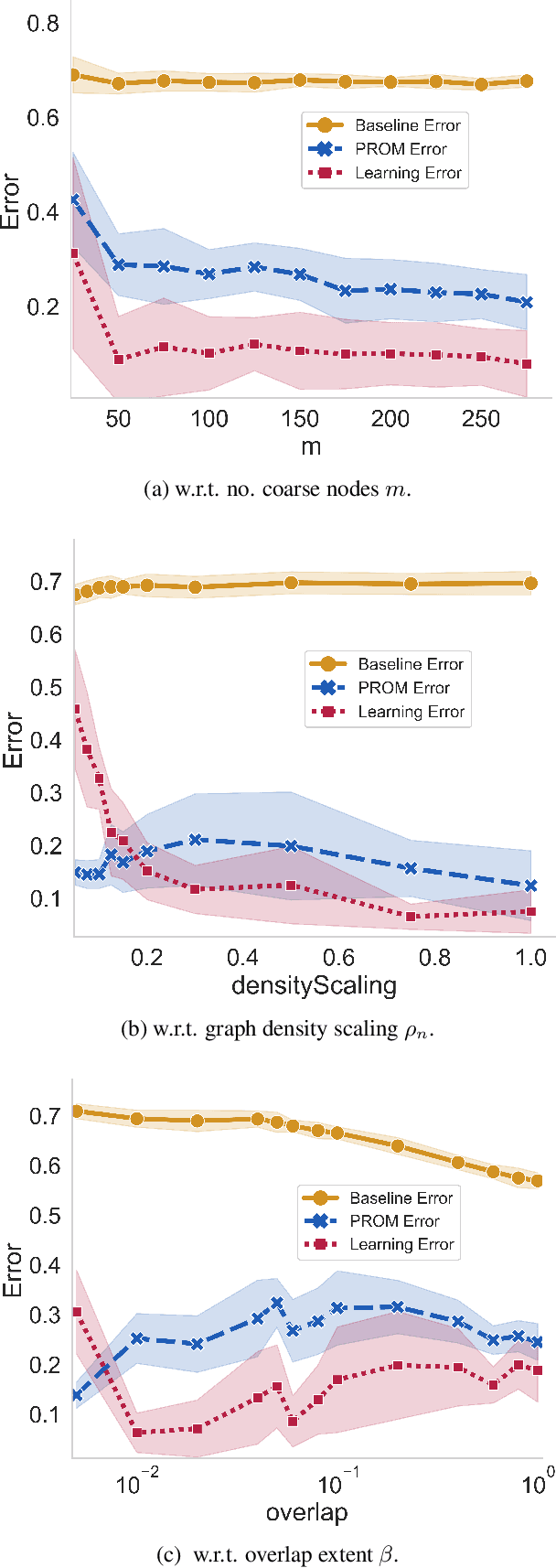
We consider the controllability of large-scale linear networked dynamical systems when complete knowledge of network structure is unavailable and knowledge is limited to coarse summaries. We provide conditions under which average controllability of the fine-scale system can be well approximated by average controllability of the (synthesized, reduced-order) coarse-scale system. To this end, we require knowledge of some inherent parametric structure of the fine-scale network that makes this type of approximation possible. Therefore, we assume that the underlying fine-scale network is generated by the stochastic block model (SBM) -- often studied in community detection. We then provide an algorithm that directly estimates the average controllability of the fine-scale system using a coarse summary of SBM. Our analysis indicates the necessity of underlying structure (e.g., in-built communities) to be able to quantify accurately the controllability from coarsely characterized networked dynamics. We also compare our method to that of the reduced-order method and highlight the regimes where both can outperform each other. Finally, we provide simulations to confirm our theoretical results for different scalings of network size and density, and the parameter that captures how much community-structure is retained in the coarse summary.

Learning the Structure of Large Networked Systems Obeying Conservation Laws

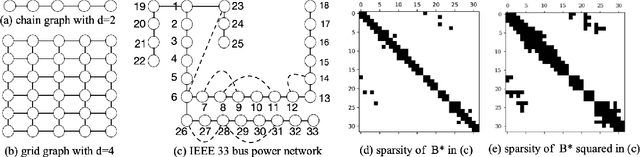
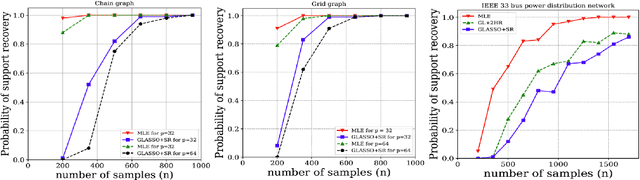
Many networked systems such as electric networks, the brain, and social networks of opinion dynamics are known to obey conservation laws. Examples of this phenomenon include the Kirchoff laws in electric networks and opinion consensus in social networks. Conservation laws in networked systems may be modeled as balance equations of the form $X = B^{*} Y$, where the sparsity pattern of $B^{*}$ captures the connectivity of the network, and $Y, X \in \mathbb{R}^p$ are vectors of "potentials" and "injected flows" at the nodes respectively. The node potentials $Y$ cause flows across edges and the flows $X$ injected at the nodes are extraneous to the network dynamics. In several practical systems, the network structure is often unknown and needs to be estimated from data. Towards this, one has access to samples of the node potentials $Y$, but only the statistics of the node injections $X$. Motivated by this important problem, we study the estimation of the sparsity structure of the matrix $B^{*}$ from $n$ samples of $Y$ under the assumption that the node injections $X$ follow a Gaussian distribution with a known covariance $\Sigma_X$. We propose a new $\ell_{1}$-regularized maximum likelihood estimator for this problem in the high-dimensional regime where the size of the network $p$ is larger than sample size $n$. We show that this optimization problem is convex in the objective and admits a unique solution. Under a new mutual incoherence condition, we establish sufficient conditions on the triple $(n,p,d)$ for which exact sparsity recovery of $B^{*}$ is possible with high probability; $d$ is the degree of the graph. We also establish guarantees for the recovery of $B^{*}$ in the element-wise maximum, Frobenius, and operator norms. Finally, we complement these theoretical results with experimental validation of the performance of the proposed estimator on synthetic and real-world data.

A Machine Learning Framework for Event Identification via Modal Analysis of PMU Data

Power systems are prone to a variety of events (e.g. line trips and generation loss) and real-time identification of such events is crucial in terms of situational awareness, reliability, and security. Using measurements from multiple synchrophasors, i.e., phasor measurement units (PMUs), we propose to identify events by extracting features based on modal dynamics. We combine such traditional physics-based feature extraction methods with machine learning to distinguish different event types. Including all measurement channels at each PMU allows exploiting diverse features but also requires learning classification models over a high-dimensional space. To address this issue, various feature selection methods are implemented to choose the best subset of features. Using the obtained subset of features, we investigate the performance of two well-known classification models, namely, logistic regression (LR) and support vector machines (SVM) to identify generation loss and line trip events in two datasets. The first dataset is obtained from simulated generation loss and line trip events in the Texas 2000-bus synthetic grid. The second is a proprietary dataset with labeled events obtained from a large utility in the USA involving measurements from nearly 500 PMUs. Our results indicate that the proposed framework is promising for identifying the two types of events.

A label efficient two-sample test

Two-sample tests evaluate whether two samples are realizations of the same distribution (the null hypothesis) or two different distributions (the alternative hypothesis). In the traditional formulation of this problem, the statistician has access to both the measurements (feature variables) and the group variable (label variable). However, in several important applications, feature variables can be easily measured but the binary label variable is unknown and costly to obtain. In this paper, we consider this important variation on the classical two-sample test problem and pose it as a problem of obtaining the labels of only a small number of samples in service of performing a two-sample test. We devise a label efficient three-stage framework: firstly, a classifier is trained with samples uniformly labeled to model the posterior probabilities of the labels; secondly, a novel query scheme dubbed \emph{bimodal query} is used to query labels of samples from both classes with maximum posterior probabilities, and lastly, the classical Friedman-Rafsky (FR) two-sample test is performed on the queried samples. Our theoretical analysis shows that bimodal query is optimal for two-sample testing using the FR statistic under reasonable conditions and that the three-stage framework controls the Type I error. Extensive experiments performed on synthetic, benchmark, and application-specific datasets demonstrate that the three-stage framework has decreased Type II error over uniform querying and certainty-based querying with same number of labels while controlling the Type I error. Source code for our algorithms and experimental results is available at https://github.com/wayne0908/Label-Efficient-Two-Sample.

Pure Exploration in Multi-armed Bandits with Graph Side Information

We study pure exploration in multi-armed bandits with graph side-information. In particular, we consider the best arm (and near-best arm) identification problem in the fixed confidence setting under the assumption that the arm rewards are smooth with respect to a given arbitrary graph. This captures a range of real world pure-exploration scenarios where one often has information about the similarity of the options or actions under consideration. We propose a novel algorithm GRUB (GRaph based UcB) for this problem and provide a theoretical characterization of its performance that elicits the benefit of the graph-side information. We complement our theory with experimental results that show that capitalizing on available graph side information yields significant improvements over pure exploration methods that are unable to use this information.