Learning Networks from Wide-Sense Stationary Stochastic Processes

Complex networked systems driven by latent inputs are common in fields like neuroscience, finance, and engineering. A key inference problem here is to learn edge connectivity from node outputs (potentials). We focus on systems governed by steady-state linear conservation laws: $X_t = {L^{\ast}}Y_{t}$, where $X_t, Y_t \in \mathbb{R}^p$ denote inputs and potentials, respectively, and the sparsity pattern of the $p \times p$ Laplacian $L^{\ast}$ encodes the edge structure. Assuming $X_t$ to be a wide-sense stationary stochastic process with a known spectral density matrix, we learn the support of $L^{\ast}$ from temporally correlated samples of $Y_t$ via an $\ell_1$-regularized Whittle's maximum likelihood estimator (MLE). The regularization is particularly useful for learning large-scale networks in the high-dimensional setting where the network size $p$ significantly exceeds the number of samples $n$. We show that the MLE problem is strictly convex, admitting a unique solution. Under a novel mutual incoherence condition and certain sufficient conditions on $(n, p, d)$, we show that the ML estimate recovers the sparsity pattern of $L^\ast$ with high probability, where $d$ is the maximum degree of the graph underlying $L^{\ast}$. We provide recovery guarantees for $L^\ast$ in element-wise maximum, Frobenius, and operator norms. Finally, we complement our theoretical results with several simulation studies on synthetic and benchmark datasets, including engineered systems (power and water networks), and real-world datasets from neural systems (such as the human brain).

Optimization Proxies using Limited Labeled Data and Training Time -- A Semi-Supervised Bayesian Neural Network Approach

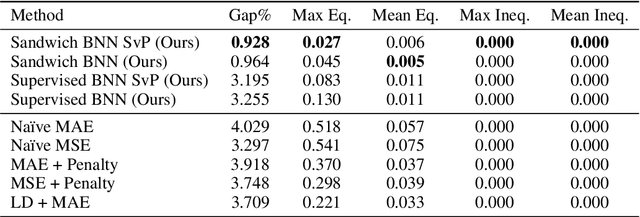
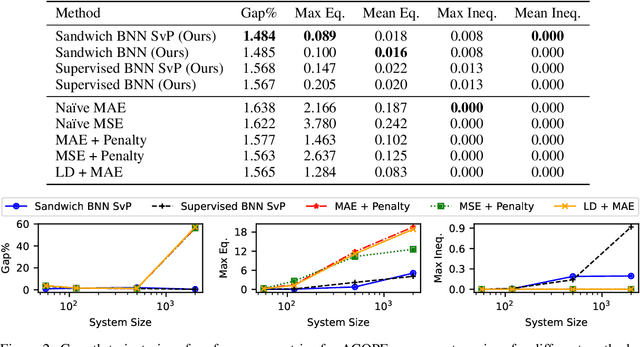
Constrained optimization problems arise in various engineering system operations such as inventory management and electric power grids. However, the requirement to repeatedly solve such optimization problems with uncertain parameters poses a significant computational challenge. This work introduces a learning scheme using Bayesian Neural Networks (BNNs) to solve constrained optimization problems under limited labeled data and restricted model training times. We propose a semi-supervised BNN for this practical but complex regime, wherein training commences in a sandwiched fashion, alternating between a supervised learning step (using labeled data) for minimizing cost, and an unsupervised learning step (using unlabeled data) for enforcing constraint feasibility. Both supervised and unsupervised steps use a Bayesian approach, where Stochastic Variational Inference is employed for approximate Bayesian inference. We show that the proposed semi-supervised learning method outperforms conventional BNN and deep neural network (DNN) architectures on important non-convex constrained optimization problems from energy network operations, achieving up to a tenfold reduction in expected maximum equality gap and halving the optimality and inequality (feasibility) gaps, without requiring any correction or projection step. By leveraging the BNN's ability to provide posterior samples at minimal computational cost, we demonstrate that a Selection via Posterior (SvP) scheme can further reduce equality gaps by more than 10%. We also provide tight and practically meaningful probabilistic confidence bounds that can be constructed using a low number of labeled testing data and readily adapted to other applications.

Equitable Routing -- Rethinking the Multiple Traveling Salesman Problem

The Multiple Traveling Salesman Problem (MTSP) with a single depot is a generalization of the well-known Traveling Salesman Problem (TSP) that involves an additional parameter, namely, the number of salesmen. In the MTSP, several salesmen at the depot need to visit a set of interconnected targets, such that each target is visited precisely once by at most one salesman while minimizing the total length of their tours. An equally important variant of the MTSP, the min-max MTSP, aims to distribute the workload (length of the individual tours) among salesmen by requiring the longest tour of all the salesmen to be as short as possible, i.e., minimizing the maximum tour length among all salesmen. The min-max MTSP appears in real-life applications to ensure a good balance of workloads for the salesmen. It is known in the literature that the min-max MTSP is notoriously difficult to solve to optimality due to the poor lower bounds its linear relaxations provide. In this paper, we formulate two novel parametric variants of the MTSP called the "fair-MTSP". One variant is formulated as a Mixed-Integer Second Order Cone Program (MISOCP), and the other as a Mixed Integer Linear Program (MILP). Both focus on enforcing the workloads for the salesmen to be equitable, i.e., the distribution of tour lengths for the salesmen to be fair while minimizing the total cost of their tours. We present algorithms to solve the two variants of the fair-MTSP to global optimality and computational results on benchmark and real-world test instances that make a case for fair-MTSP as a viable alternative to the min-max MTSP.

Data-Efficient Power Flow Learning for Network Contingencies

This work presents an efficient data-driven method to learn power flows in grids with network contingencies and to estimate corresponding probabilistic voltage envelopes (PVE). First, a network-aware Gaussian process (GP) termed Vertex-Degree Kernel (VDK-GP), developed in prior work, is used to estimate voltage-power functions for a few network configurations. The paper introduces a novel multi-task vertex degree kernel (MT-VDK) that amalgamates the learned VDK-GPs to determine power flows for unseen networks, with a significant reduction in the computational complexity and hyperparameter requirements compared to alternate approaches. Simulations on the IEEE 30-Bus network demonstrate the retention and transfer of power flow knowledge in both N-1 and N-2 contingency scenarios. The MT-VDK-GP approach achieves over 50% reduction in mean prediction error for novel N-1 contingency network configurations in low training data regimes (50-250 samples) over VDK-GP. Additionally, MT-VDK-GP outperforms a hyper-parameter based transfer learning approach in over 75% of N-2 contingency network structures, even without historical N-2 outage data. The proposed method demonstrates the ability to achieve PVEs using sixteen times fewer power flow solutions compared to Monte-Carlo sampling-based methods.

Information Theoretically Optimal Sample Complexity of Learning Dynamical Directed Acyclic Graphs

In this article, the optimal sample complexity of learning the underlying interaction/dependencies of a Linear Dynamical System (LDS) over a Directed Acyclic Graph (DAG) is studied. The sample complexity of learning a DAG's structure is well-studied for static systems, where the samples of nodal states are independent and identically distributed (i.i.d.). However, such a study is less explored for DAGs with dynamical systems, where the nodal states are temporally correlated. We call such a DAG underlying an LDS as \emph{dynamical} DAG (DDAG). In particular, we consider a DDAG where the nodal dynamics are driven by unobserved exogenous noise sources that are wide-sense stationary (WSS) in time but are mutually uncorrelated, and have the same {power spectral density (PSD)}. Inspired by the static settings, a metric and an algorithm based on the PSD matrix of the observed time series are proposed to reconstruct the DDAG. The equal noise PSD assumption can be relaxed such that identifiability conditions for DDAG reconstruction are not violated. For the LDS with WSS (sub) Gaussian exogenous noise sources, it is shown that the optimal sample complexity (or length of state trajectory) needed to learn the DDAG is $n=\Theta(q\log(p/q))$, where $p$ is the number of nodes and $q$ is the maximum number of parents per node. To prove the sample complexity upper bound, a concentration bound for the PSD estimation is derived, under two different sampling strategies. A matching min-max lower bound using generalized Fano's inequality also is provided, thus showing the order optimality of the proposed algorithm.

Graph-Structured Kernel Design for Power Flow Learning using Gaussian Processes

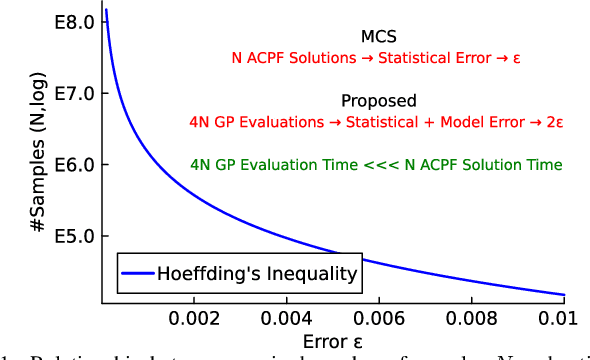
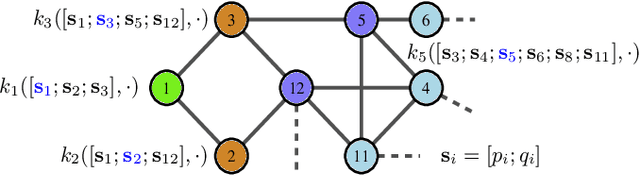
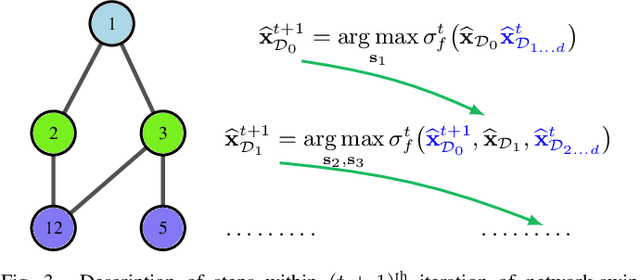
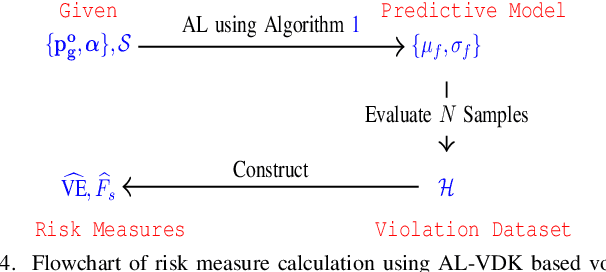
This paper presents a physics-inspired graph-structured kernel designed for power flow learning using Gaussian Process (GP). The kernel, named the vertex-degree kernel (VDK), relies on latent decomposition of voltage-injection relationship based on the network graph or topology. Notably, VDK design avoids the need to solve optimization problems for kernel search. To enhance efficiency, we also explore a graph-reduction approach to obtain a VDK representation with lesser terms. Additionally, we propose a novel network-swipe active learning scheme, which intelligently selects sequential training inputs to accelerate the learning of VDK. Leveraging the additive structure of VDK, the active learning algorithm performs a block-descent type procedure on GP's predictive variance, serving as a proxy for information gain. Simulations demonstrate that the proposed VDK-GP achieves more than two fold sample complexity reduction, compared to full GP on medium scale 500-Bus and large scale 1354-Bus power systems. The network-swipe algorithm outperforms mean performance of 500 random trials on test predictions by two fold for medium-sized 500-Bus systems and best performance of 25 random trials for large-scale 1354-Bus systems by 10%. Moreover, we demonstrate that the proposed method's performance for uncertainty quantification applications with distributionally shifted testing data sets.

GP CC-OPF: Gaussian Process based optimization tool for Chance-Constrained Optimal Power Flow

The Gaussian Process (GP) based Chance-Constrained Optimal Power Flow (CC-OPF) is an open-source Python code developed for solving economic dispatch (ED) problem in modern power grids. In recent years, integrating a significant amount of renewables into a power grid causes high fluctuations and thus brings a lot of uncertainty to power grid operations. This fact makes the conventional model-based CC-OPF problem non-convex and computationally complex to solve. The developed tool presents a novel data-driven approach based on the GP regression model for solving the CC-OPF problem with a trade-off between complexity and accuracy. The proposed approach and developed software can help system operators to effectively perform ED optimization in the presence of large uncertainties in the power grid.

Data-Driven Chance Constrained AC-OPF using Hybrid Sparse Gaussian Processes

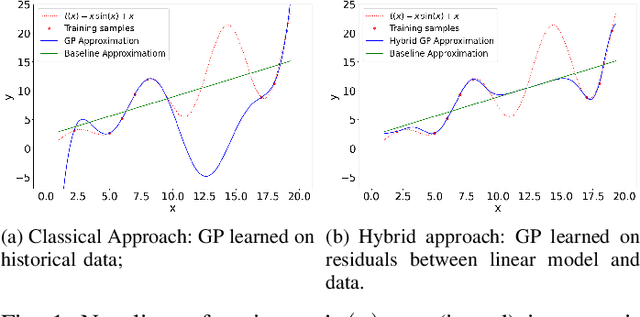
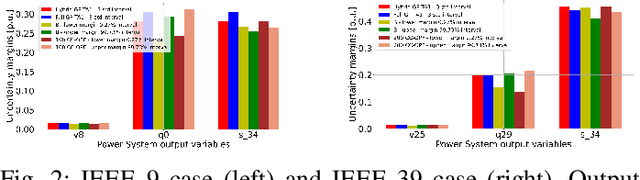
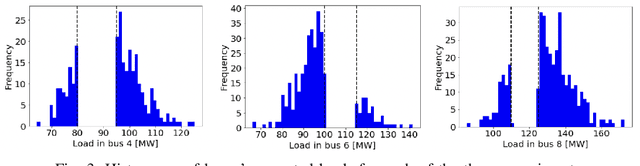
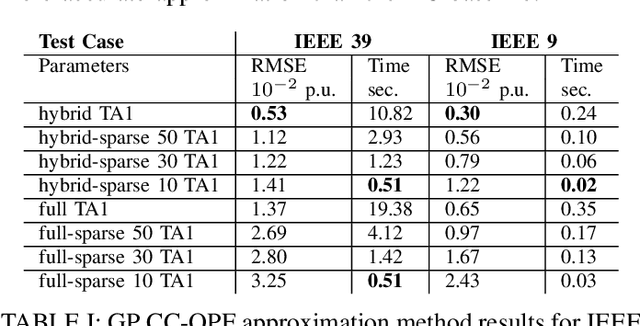
The alternating current (AC) chance-constrained optimal power flow (CC-OPF) problem addresses the economic efficiency of electricity generation and delivery under generation uncertainty. The latter is intrinsic to modern power grids because of the high amount of renewables. Despite its academic success, the AC CC-OPF problem is highly nonlinear and computationally demanding, which limits its practical impact. For improving the AC-OPF problem complexity/accuracy trade-off, the paper proposes a fast data-driven setup that uses the sparse and hybrid Gaussian processes (GP) framework to model the power flow equations with input uncertainty. We advocate the efficiency of the proposed approach by a numerical study over multiple IEEE test cases showing up to two times faster and more accurate solutions compared to the state-of-the-art methods.

Learning Distribution Grid Topologies: A Tutorial

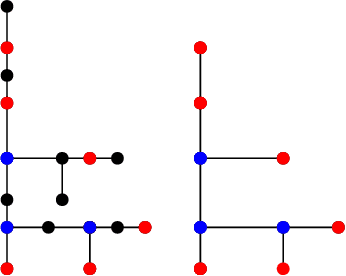
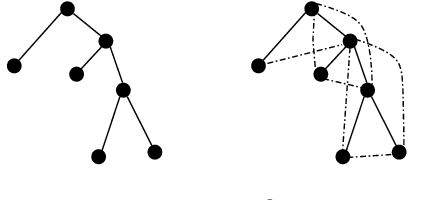
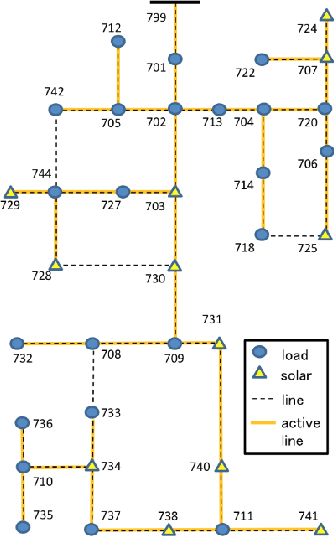
Unveiling feeder topologies from data is of paramount importance to advance situational awareness and proper utilization of smart resources in power distribution grids. This tutorial summarizes, contrasts, and establishes useful links between recent works on topology identification and detection schemes that have been proposed for power distribution grids.% under different regimes of measurement type, observability, and sampling. The primary focus is to highlight methods that overcome the limited availability of measurement devices in distribution grids, while enhancing topology estimates using conservation laws of power-flow physics and structural properties of feeders. Grid data from phasor measurement units or smart meters can be collected either passively in the traditional way, or actively, upon actuating grid resources and measuring the feeder's voltage response. Analytical claims on feeder identifiability and detectability are reviewed under disparate meter placement scenarios. Such topology learning claims can be attained exactly or approximately so via algorithmic solutions with various levels of computational complexity, ranging from least-squares fits to convex optimization problems, and from polynomial-time searches over graphs to mixed-integer programs. This tutorial aspires to provide researchers and engineers with knowledge of the current state-of-the-art in tractable distribution grid learning and insights into future directions of work.

Detecting Anomalies using Overlapping Electrical Measurements in Smart Power Grids

As cyber-attacks against critical infrastructure become more frequent, it is increasingly important to be able to rapidly identify and respond to these threats. This work investigates two independent systems with overlapping electrical measurements with the goal to more rapidly identify anomalies. The independent systems include HIST, a SCADA historian, and ION, an automatic meter reading system (AMR). While prior research has explored the benefits of fusing measurements, the possibility of overlapping measurements from an existing electrical system has not been investigated. To that end, we explore the potential benefits of combining overlapping measurements both to improve the speed/accuracy of anomaly detection and to provide additional validation of the collected measurements. In this paper, we show that merging overlapping measurements provide a more holistic picture of the observed systems. By applying Dynamic Time Warping more anomalies were found -- specifically, an average of 349 times more anomalies, when considering anomalies from both overlapping measurements. When merging the overlapping measurements, a percent change of anomalies of up to 785\% can be achieved compared to a non-merge of the data as reflected by experimental results.