Optimization Proxies using Limited Labeled Data and Training Time -- A Semi-Supervised Bayesian Neural Network Approach

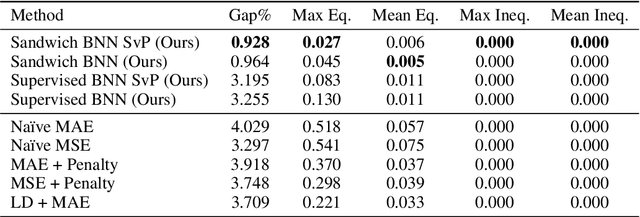
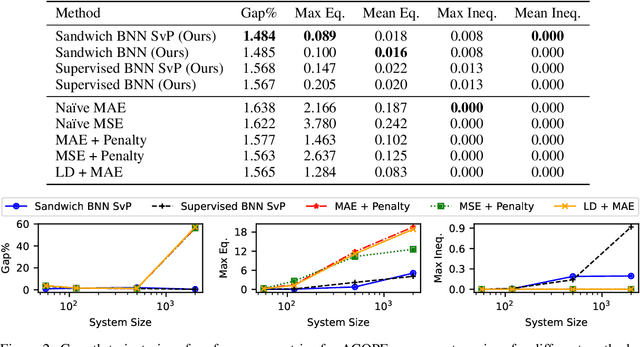
Constrained optimization problems arise in various engineering system operations such as inventory management and electric power grids. However, the requirement to repeatedly solve such optimization problems with uncertain parameters poses a significant computational challenge. This work introduces a learning scheme using Bayesian Neural Networks (BNNs) to solve constrained optimization problems under limited labeled data and restricted model training times. We propose a semi-supervised BNN for this practical but complex regime, wherein training commences in a sandwiched fashion, alternating between a supervised learning step (using labeled data) for minimizing cost, and an unsupervised learning step (using unlabeled data) for enforcing constraint feasibility. Both supervised and unsupervised steps use a Bayesian approach, where Stochastic Variational Inference is employed for approximate Bayesian inference. We show that the proposed semi-supervised learning method outperforms conventional BNN and deep neural network (DNN) architectures on important non-convex constrained optimization problems from energy network operations, achieving up to a tenfold reduction in expected maximum equality gap and halving the optimality and inequality (feasibility) gaps, without requiring any correction or projection step. By leveraging the BNN's ability to provide posterior samples at minimal computational cost, we demonstrate that a Selection via Posterior (SvP) scheme can further reduce equality gaps by more than 10%. We also provide tight and practically meaningful probabilistic confidence bounds that can be constructed using a low number of labeled testing data and readily adapted to other applications.

$A^*$ for Graphs of Convex Sets

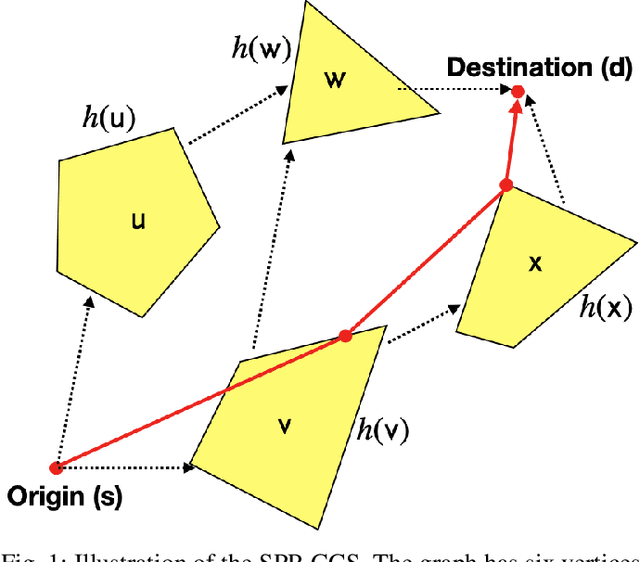
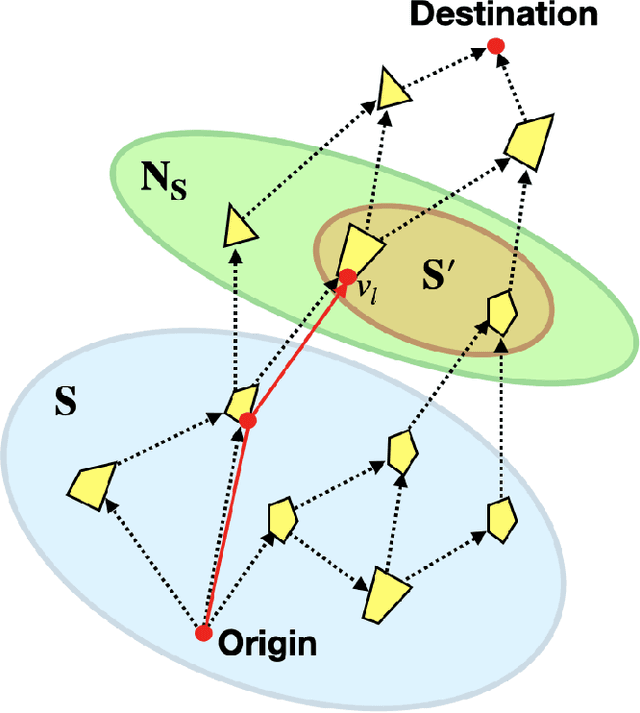
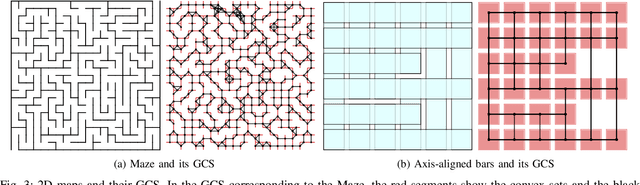
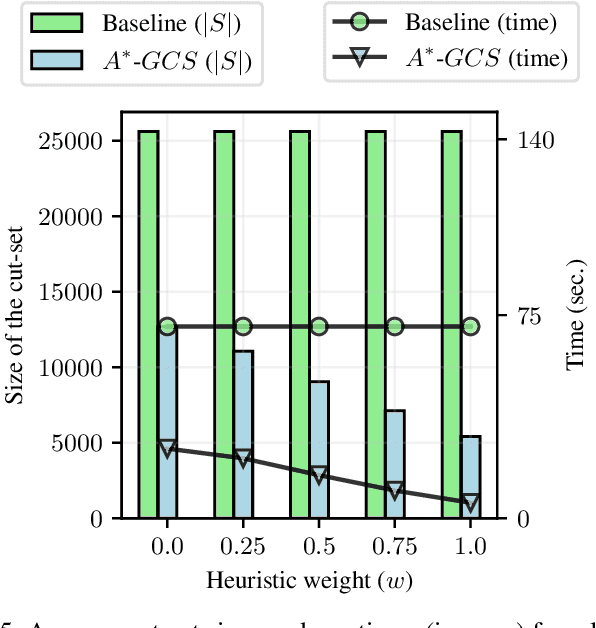
We present a novel algorithm that fuses the existing convex-programming based approach with heuristic information to find optimality guarantees and near-optimal paths for the Shortest Path Problem in the Graph of Convex Sets (SPP-GCS). Our method, inspired by $A^*$, initiates a best-first-like procedure from a designated subset of vertices and iteratively expands it until further growth is neither possible nor beneficial. Traditionally, obtaining solutions with bounds for an optimization problem involves solving a relaxation, modifying the relaxed solution to a feasible one, and then comparing the two solutions to establish bounds. However, for SPP-GCS, we demonstrate that reversing this process can be more advantageous, especially with Euclidean travel costs. In other words, we initially employ $A^*$ to find a feasible solution for SPP-GCS, then solve a convex relaxation restricted to the vertices explored by $A^*$ to obtain a relaxed solution, and finally, compare the solutions to derive bounds. We present numerical results to highlight the advantages of our algorithm over the existing approach in terms of the sizes of the convex programs solved and computation time.

Equitable Routing -- Rethinking the Multiple Traveling Salesman Problem

The Multiple Traveling Salesman Problem (MTSP) with a single depot is a generalization of the well-known Traveling Salesman Problem (TSP) that involves an additional parameter, namely, the number of salesmen. In the MTSP, several salesmen at the depot need to visit a set of interconnected targets, such that each target is visited precisely once by at most one salesman while minimizing the total length of their tours. An equally important variant of the MTSP, the min-max MTSP, aims to distribute the workload (length of the individual tours) among salesmen by requiring the longest tour of all the salesmen to be as short as possible, i.e., minimizing the maximum tour length among all salesmen. The min-max MTSP appears in real-life applications to ensure a good balance of workloads for the salesmen. It is known in the literature that the min-max MTSP is notoriously difficult to solve to optimality due to the poor lower bounds its linear relaxations provide. In this paper, we formulate two novel parametric variants of the MTSP called the "fair-MTSP". One variant is formulated as a Mixed-Integer Second Order Cone Program (MISOCP), and the other as a Mixed Integer Linear Program (MILP). Both focus on enforcing the workloads for the salesmen to be equitable, i.e., the distribution of tour lengths for the salesmen to be fair while minimizing the total cost of their tours. We present algorithms to solve the two variants of the fair-MTSP to global optimality and computational results on benchmark and real-world test instances that make a case for fair-MTSP as a viable alternative to the min-max MTSP.

Deep Reinforcement Learning-Based Approach for a Single Vehicle Persistent Surveillance Problem with Fuel Constraints

This article presents a deep reinforcement learning-based approach to tackle a persistent surveillance mission requiring a single unmanned aerial vehicle initially stationed at a depot with fuel or time-of-flight constraints to repeatedly visit a set of targets with equal priority. Owing to the vehicle's fuel or time-of-flight constraints, the vehicle must be regularly refueled, or its battery must be recharged at the depot. The objective of the problem is to determine an optimal sequence of visits to the targets that minimizes the maximum time elapsed between successive visits to any target while ensuring that the vehicle never runs out of fuel or charge. We present a deep reinforcement learning algorithm to solve this problem and present the results of numerical experiments that corroborate the effectiveness of this approach in comparison with common-sense greedy heuristics.

Deployable, Data-Driven Unmanned Vehicle Navigation System in GPS-Denied, Feature-Deficient Environments

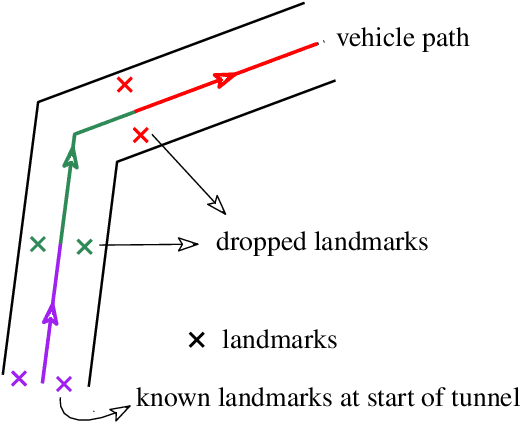
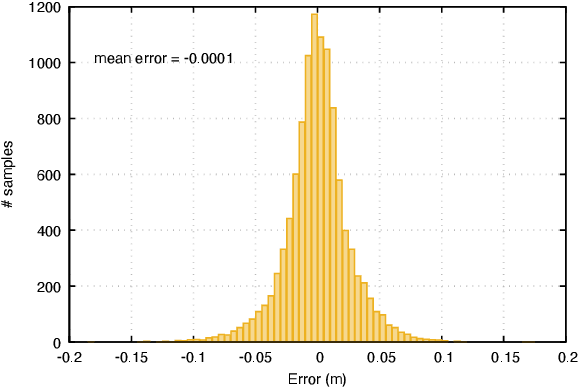
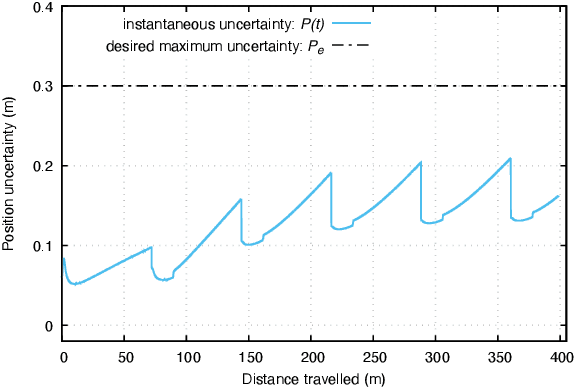
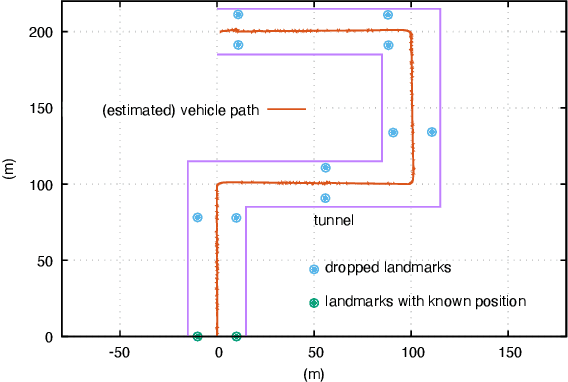
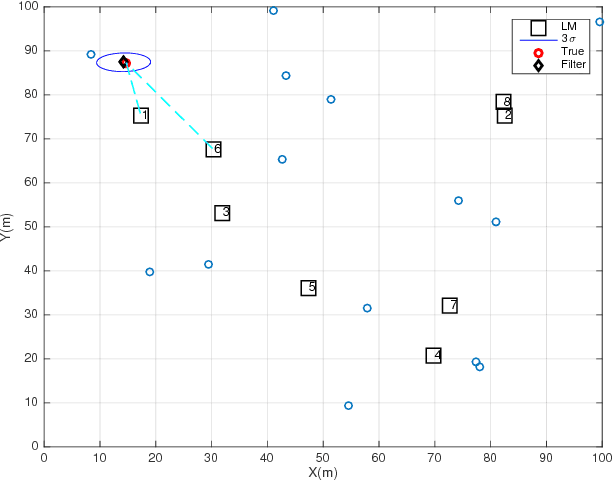
This paper presents a novel data-driven navigation system to navigate an Unmanned Vehicle (UV) in GPS-denied, feature-deficient environments such as tunnels, or mines. The method utilizes Radio Frequency Identification (RFID) tags, also referred to as landmarks, as range sensors that are carried by the vehicle and are deployed in the environment to enable localization as the vehicle traverses its pre-defined path through the tunnel. A key question that arises in such scenario is to estimate and reduce the number of landmarks required for localization before the start of the mission, given some information about the environment. The main constraint of the problem is to keep the maximum uncertainty in the position estimate near a desired value. In this article, we combine techniques from estimation, machine learning, and mixed-integer convex optimization to develop a systematic method to perform localization and navigate the UV through the environment while ensuring minimum number of landmarks are used and all the mission constraints are satisfied.

Cooperative Planning for Fuel-constrained Aerial Vehicles and Ground-based Refueling Vehicles for Large-Scale Coverage

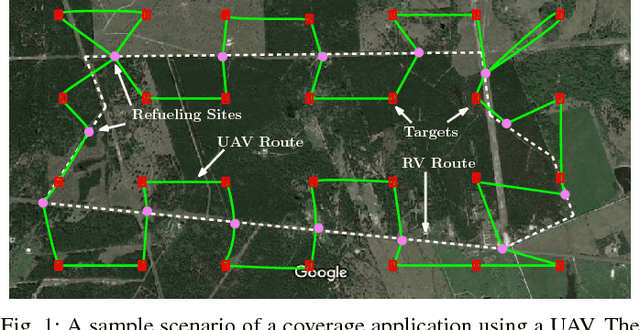
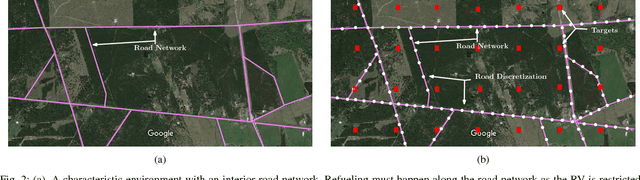
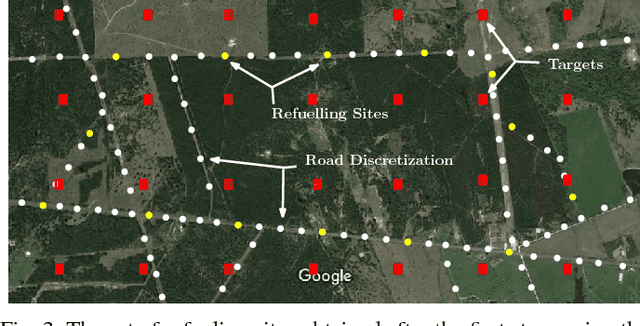
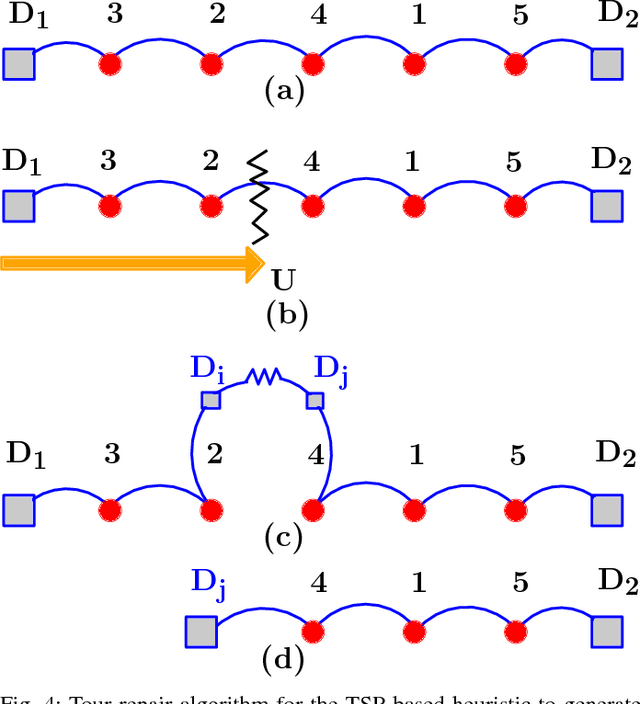
Low cost Unmanned Aerial Vehicles (UAVs) need multiple refuels to accomplish large area coverage. The number of refueling stations and their placement plays a vital role in determining coverage efficiency. In this paper, we propose the use of a ground-based refueling vehicle (RV) to increase the operational range of a UAV in both spatial and temporal domains. Determining optimal routes for the UAV and RV, and selecting optimized locations for refueling to aid in minimizing coverage time is a challenging problem due to different vehicle speeds, coupling between refueling location placement, and the coverage area at each location. We develop a two-stage strategy for coupled route planning for UAV and RV to perform a coverage mission. The first stage computes a minimal set of refueling sites that permit a feasible UAV route. In the second stage, multiple Mixed-Integer Linear Programming (MILP) formulations are developed to plan optimal routes for the UAV and the refueling vehicle taking into account the feasible set of refueling sites generated in stage one. The performance of different formulations is compared empirically. In addition, computationally efficient heuristics are developed to solve the routing problem. Extensive simulations are conducted to corroborate the effectiveness of proposed approaches.

Routing Unmanned Vehicles in GPS-Denied Environments

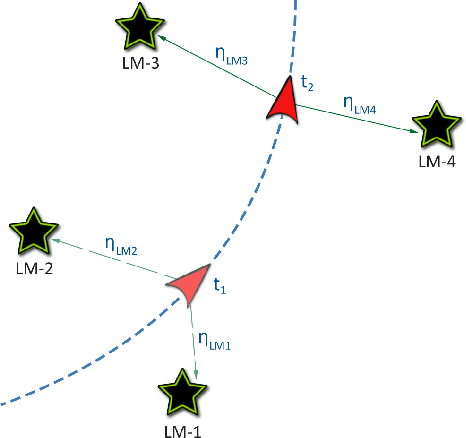
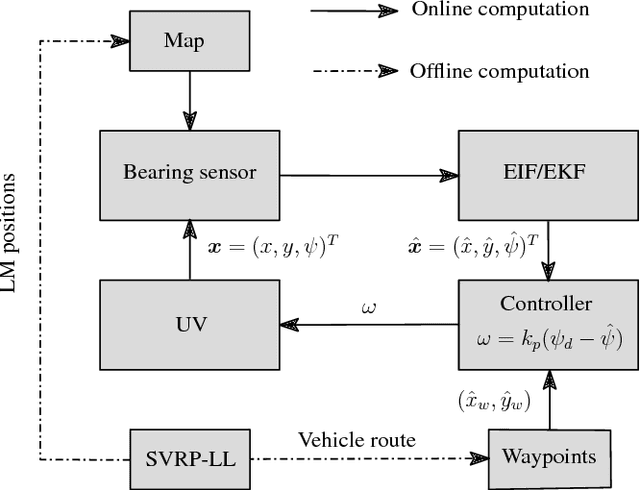
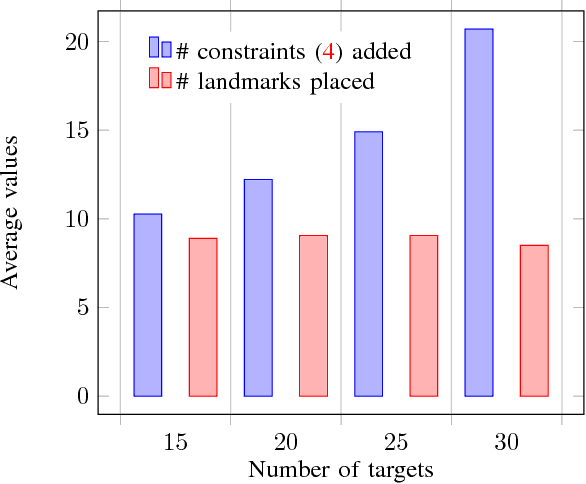
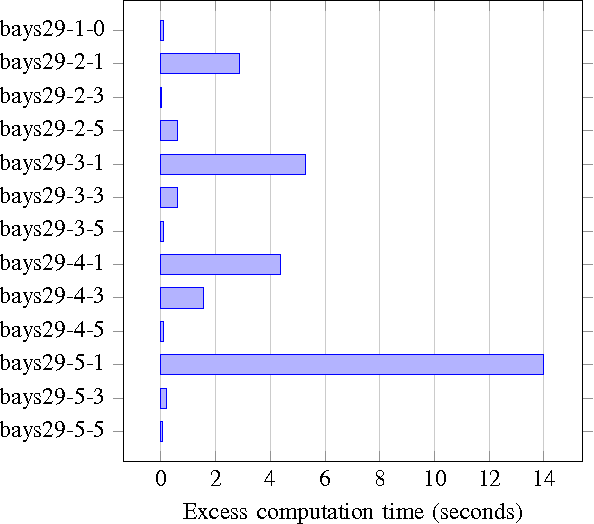
Most of the routing algorithms for unmanned vehicles, that arise in data gathering and monitoring applications in the literature, rely on the Global Positioning System (GPS) information for localization. However, disruption of GPS signals either intentionally or unintentionally could potentially render these algorithms not applicable. In this article, we present a novel method to address this difficulty by combining methods from cooperative localization and routing. In particular, the article formulates a fundamental combinatorial optimization problem to plan routes for an unmanned vehicle in a GPS-restricted environment while enabling localization for the vehicle. We also develop algorithms to compute optimal paths for the vehicle using the proposed formulation. Extensive simulation results are also presented to corroborate the effectiveness and performance of the proposed formulation and algorithms.

Path Planning for Multiple Heterogeneous Unmanned Vehicles with Uncertain Service Times

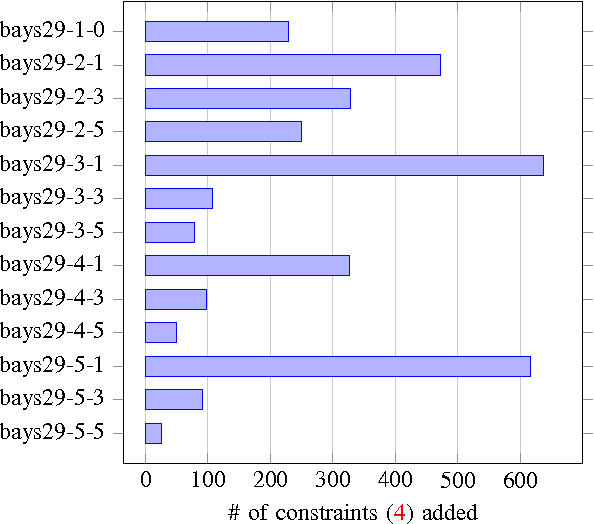
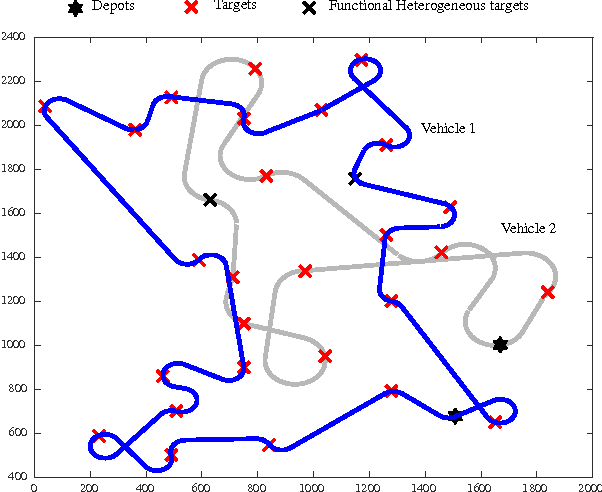
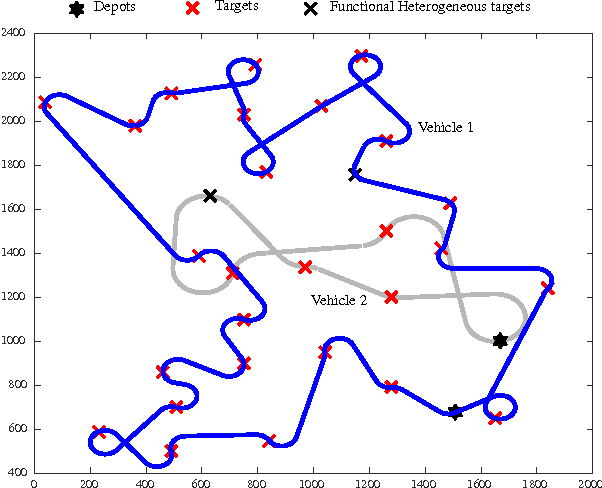
This article presents a framework and develops a formulation to solve a path planning problem for multiple heterogeneous Unmanned Vehicles (UVs) with uncertain service times for each vehicle--target pair. The vehicles incur a penalty proportional to the duration of their total service time in excess of a preset constant. The vehicles differ in their motion constraints and are located at distinct depots at the start of the mission. The vehicles may also be equipped with disparate sensors. The objective is to find a tour for each vehicle that starts and ends at its respective depot such that every target is visited and serviced by some vehicle while minimizing the sum of the total travel distance and the expected penalty incurred by all the vehicles. We formulate the problem as a two-stage stochastic program with recourse, present the theoretical properties of the formulation and advantages of using such a formulation, as opposed to a deterministic expected value formulation, to solve the problem. Extensive numerical simulations also corroborate the effectiveness of the proposed approach.