COLREGs Compliant Collision Avoidance and Grounding Prevention for Autonomous Marine Navigation

Maritime Autonomous Surface Ships (MASS) are increasingly regarded as a promising solution to address crew shortages, improve navigational safety, and improve operational efficiency in the maritime industry. Nevertheless, the reliable deployment of MASS in real-world environments remains a significant challenge, particularly in congested waters where the majority of maritime accidents occur. This emphasizes the need for safe and regulation-aware motion planning strategies for MASS that are capable of operating under dynamic maritime conditions. This paper presents a unified motion planning method for MASS that achieves real time collision avoidance, compliance with International Regulations for Preventing Collisions at Sea (COLREGs), and grounding prevention. The proposed work introduces a convex optimization method that integrates velocity obstacle-based (VO) collision constraints, COLREGs-based directional constraints, and bathymetry-based grounding constraints to generate computationally efficient, rule-compliant optimal velocity selection. To enhance robustness, the classical VO method is extended to consider uncertainty in the position and velocity estimates of the target vessel. Unnavigable shallow water regions obtained from bathymetric data, which are inherently nonconvex, are approximated via convex geometries using a integer linear programming (ILP), allowing grounding constraints to be incorporated into the motion planning. The resulting optimization generates optimal and dynamically feasible input velocities that meet collision avoidance, regulatory compliance, kinodynamic limits, and grounding prevention requirements. Simulation results involving multi-vessel encounters demonstrate the effectiveness of the proposed method in producing safe and regulation-compliant maneuvers, highlighting the suitability of the proposed approach for real time autonomous maritime navigation.

A Robust Simulation Framework for Verification and Validation of Autonomous Maritime Navigation in Adverse Weather and Constrained Environments

Maritime Autonomous Surface Ships (MASS) have emerged as a promising solution to enhance navigational safety, operational efficiency, and long-term cost effectiveness. However, their reliable deployment requires rigorous verification and validation (V\&V) under various environmental conditions, including extreme and safety-critical scenarios. This paper presents an enhanced virtual simulation framework to support the V\&V of MASS in realistic maritime environments, with particular emphasis on the influence of weather and bathymetry on autonomous navigation performance. The framework incorporates a high-fidelity environmental modeling suite capable of simulating adverse weather conditions such as rain, fog, and wave dynamics. The key factors that affect weather, such as rain and visibility, are parameterized to affect sea-state characteristics, perception, and sensing systems, resulting in position and velocity uncertainty, reduced visibility, and degraded situational awareness. Furthermore, high-resolution bathymetric data from major U.S. ports are integrated to enable depth-aware navigation, grounding prevention capabilities, and evaluation of vessel controllability in shallow or confined waterways. The proposed framework offers extensive configurability, enabling systematic testing in a wide spectrum of maritime conditions, including scenarios that are impractical or unsafe to replicate in real-world trials, thus supporting the V\&V of MASS.

Optimal Solutions for the Moving Target Vehicle Routing Problem via Branch-and-Price with Relaxed Continuity

The Moving Target Vehicle Routing Problem (MT-VRP) seeks trajectories for several agents that intercept a set of moving targets, subject to speed, time window, and capacity constraints. We introduce an exact algorithm, Branch-and-Price with Relaxed Continuity (BPRC), for the MT-VRP. The main challenge in a branch-and-price approach for the MT-VRP is the pricing subproblem, which is complicated by moving targets and time-dependent travel costs between targets. Our key contribution is a new labeling algorithm that solves this subproblem by means of a novel dominance criterion tailored for problems with moving targets. Numerical results on instances with up to 25 targets show that our algorithm finds optimal solutions more than an order of magnitude faster than a baseline based on previous work, showing particular strength in scenarios with limited agent capacities.

Parallel, Asymptotically Optimal Algorithms for Moving Target Traveling Salesman Problems

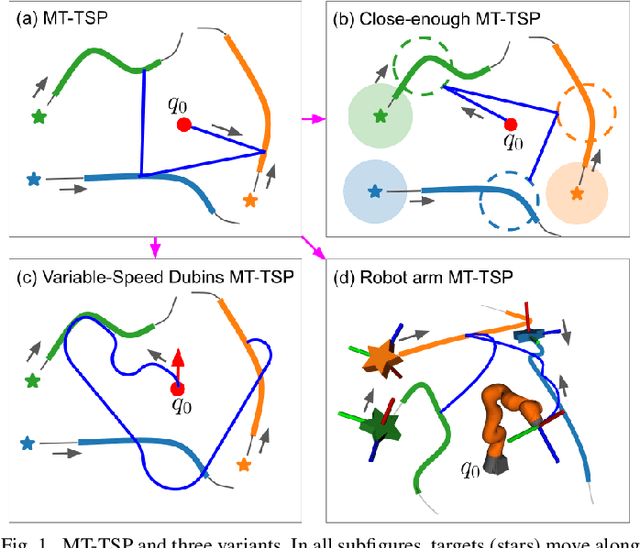
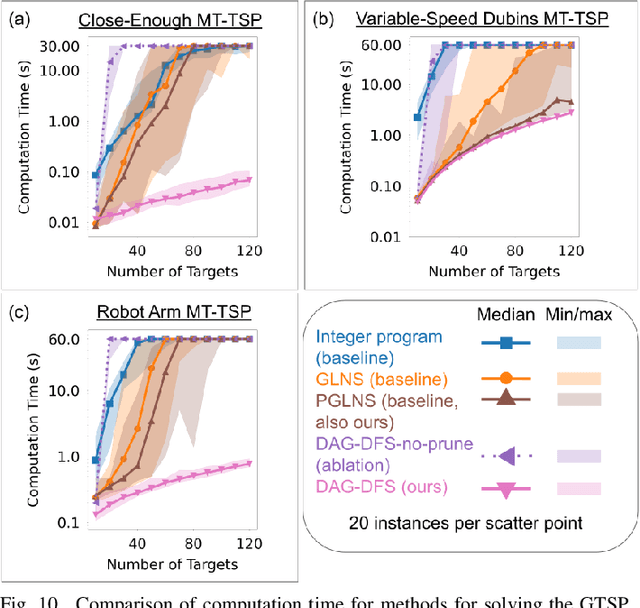
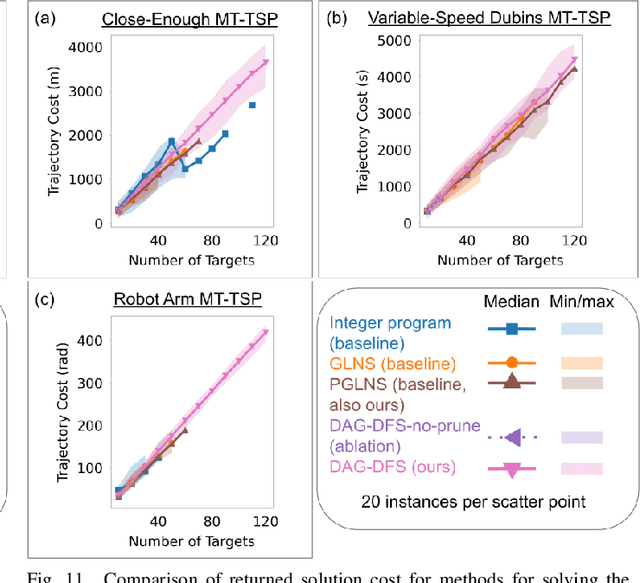
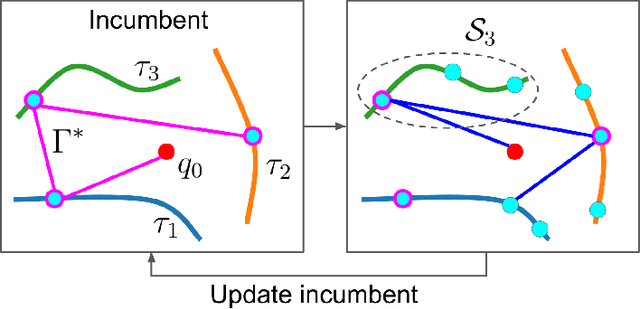
The Moving Target Traveling Salesman Problem (MT-TSP) seeks an agent trajectory that intercepts several moving targets, within a particular time window for each target. In the presence of generic nonlinear target trajectories or kinematic constraints on the agent, no prior algorithm guarantees convergence to an optimal MT-TSP solution. Therefore, we introduce the Iterated Random Generalized (IRG) TSP framework. The key idea behind IRG is to alternate between randomly sampling a set of agent configuration-time points, corresponding to interceptions of targets, and finding a sequence of interception points by solving a generalized TSP (GTSP). This alternation enables asymptotic convergence to the optimum. We introduce two parallel algorithms within the IRG framework. The first algorithm, IRG-PGLNS, solves GTSPs using PGLNS, our parallelized extension of the state-of-the-art solver GLNS. The second algorithm, Parallel Communicating GTSPs (PCG), solves GTSPs corresponding to several sets of points simultaneously. We present numerical results for three variants of the MT-TSP: one where intercepting a target only requires coming within a particular distance, another where the agent is a variable-speed Dubins car, and a third where the agent is a redundant robot arm. We show that IRG-PGLNS and PCG both converge faster than a baseline based on prior work.

A Complete and Bounded-Suboptimal Algorithm for a Moving Target Traveling Salesman Problem with Obstacles in 3D

The moving target traveling salesman problem with obstacles (MT-TSP-O) seeks an obstacle-free trajectory for an agent that intercepts a given set of moving targets, each within specified time windows, and returns to the agent's starting position. Each target moves with a constant velocity within its time windows, and the agent has a speed limit no smaller than any target's speed. We present FMC*-TSP, the first complete and bounded-suboptimal algorithm for the MT-TSP-O, and results for an agent whose configuration space is $\mathbb{R}^3$. Our algorithm interleaves a high-level search and a low-level search, where the high-level search solves a generalized traveling salesman problem with time windows (GTSP-TW) to find a sequence of targets and corresponding time windows for the agent to visit. Given such a sequence, the low-level search then finds an associated agent trajectory. To solve the low-level planning problem, we develop a new algorithm called FMC*, which finds a shortest path on a graph of convex sets (GCS) via implicit graph search and pruning techniques specialized for problems with moving targets. We test FMC*-TSP on 280 problem instances with up to 40 targets and demonstrate its smaller median runtime than a baseline based on prior work.

A Mixed-Integer Conic Program for the Multi-Agent Moving-Target Traveling Salesman Problem

The Moving-Target Traveling Salesman Problem (MT-TSP) aims to find a shortest path for an agent that starts at a stationary depot, visits a set of moving targets exactly once, each within one of their respective time windows, and then returns to the depot. In this paper, we introduce a new Mixed-Integer Conic Program (MICP) formulation that finds the optimum for the Multi-Agent Moving-Target Traveling Salesman Problem (MA-MT-TSP), a generalization of the MT-TSP involving multiple agents. We obtain our formulation by first restating the current state-of-the-art MICP formulation for MA-MT-TSP as a Mixed-Integer Nonlinear Nonconvex Program, and then reformulating it as a new MICP. We present computational results to demonstrate the performance of our approach. The results show that our formulation significantly outperforms the state-of-the-art, with up to a two-order-of-magnitude reduction in runtime, and up to over 90% tighter optimality gap.

A Complete Algorithm for a Moving Target Traveling Salesman Problem with Obstacles

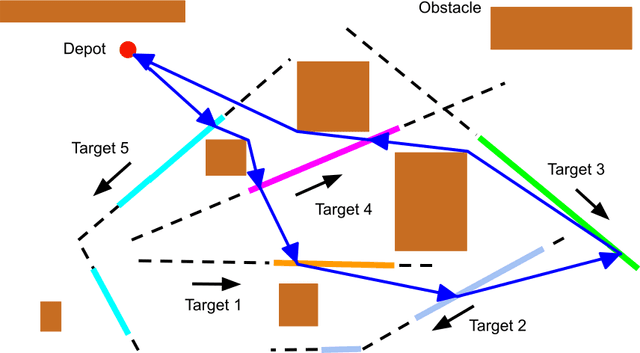
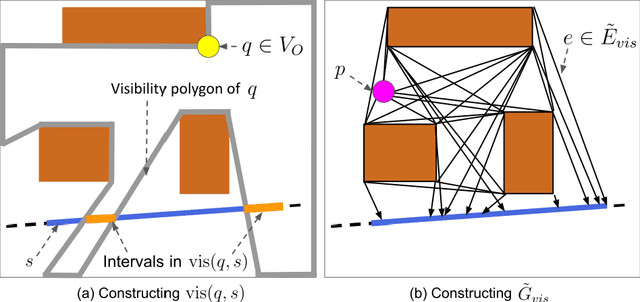
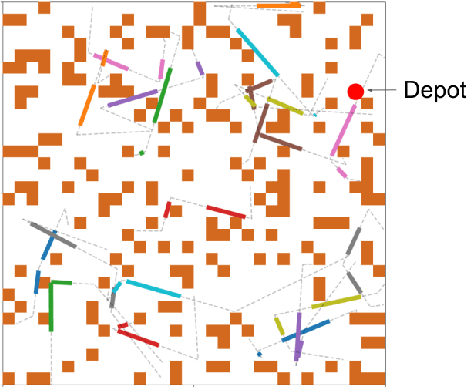
The moving target traveling salesman problem with obstacles (MT-TSP-O) is a generalization of the traveling salesman problem (TSP) where, as its name suggests, the targets are moving. A solution to the MT-TSP-O is a trajectory that visits each moving target during a certain time window(s), and this trajectory avoids stationary obstacles. We assume each target moves at a constant velocity during each of its time windows. The agent has a speed limit, and this speed limit is no smaller than any target's speed. This paper presents the first complete algorithm for finding feasible solutions to the MT-TSP-O. Our algorithm builds a tree where the nodes are agent trajectories intercepting a unique sequence of targets within a unique sequence of time windows. We generate each of a parent node's children by extending the parent's trajectory to intercept one additional target, each child corresponding to a different choice of target and time window. This extension consists of planning a trajectory from the parent trajectory's final point in space-time to a moving target. To solve this point-to-moving-target subproblem, we define a novel generalization of a visibility graph called a moving target visibility graph (MTVG). Our overall algorithm is called MTVG-TSP. To validate MTVG-TSP, we test it on 570 instances with up to 30 targets. We implement a baseline method that samples trajectories of targets into points, based on prior work on special cases of the MT-TSP-O. MTVG-TSP finds feasible solutions in all cases where the baseline does, and when the sum of the targets' time window lengths enters a critical range, MTVG-TSP finds a feasible solution with up to 38 times less computation time.

The Persistent Robot Charging Problem for Long-Duration Autonomy

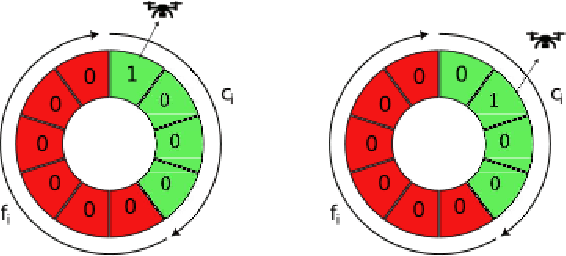
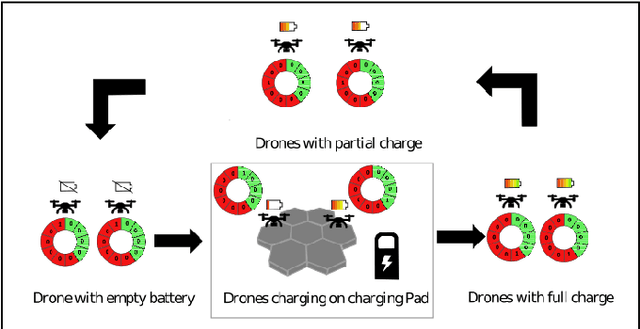
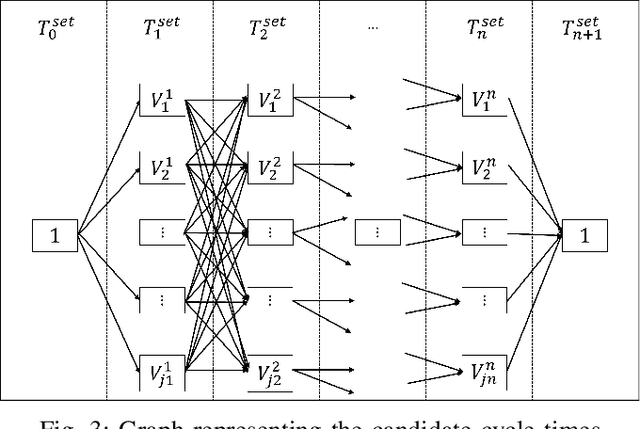
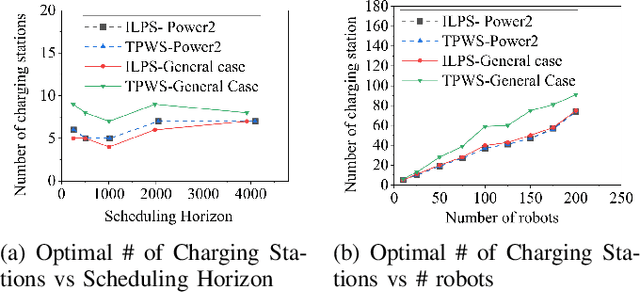
This paper introduces a novel formulation aimed at determining the optimal schedule for recharging a fleet of $n$ heterogeneous robots, with the primary objective of minimizing resource utilization. This study provides a foundational framework applicable to Multi-Robot Mission Planning, particularly in scenarios demanding Long-Duration Autonomy (LDA) or other contexts that necessitate periodic recharging of multiple robots. A novel Integer Linear Programming (ILP) model is proposed to calculate the optimal initial conditions (partial charge) for individual robots, leading to the minimal utilization of charging stations. This formulation was further generalized to maximize the servicing time for robots given adequate charging stations. The efficacy of the proposed formulation is evaluated through a comparative analysis, measuring its performance against the thrift price scheduling algorithm documented in the existing literature. The findings not only validate the effectiveness of the proposed approach but also underscore its potential as a valuable tool in optimizing resource allocation for a range of robotic and engineering applications.

$A^*$ for Graphs of Convex Sets

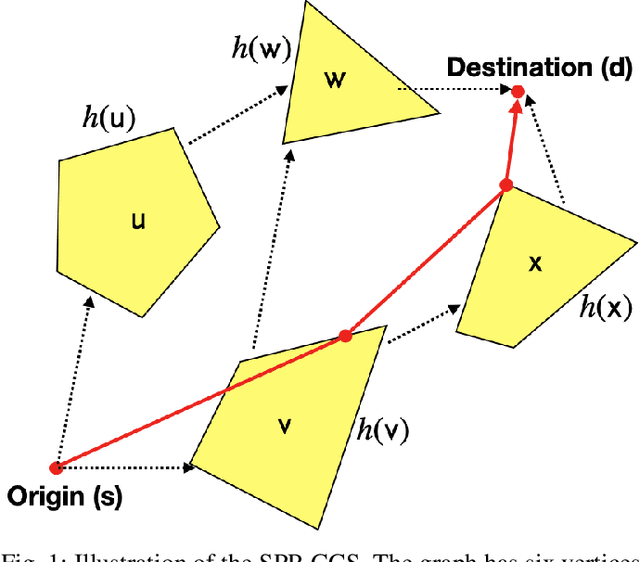
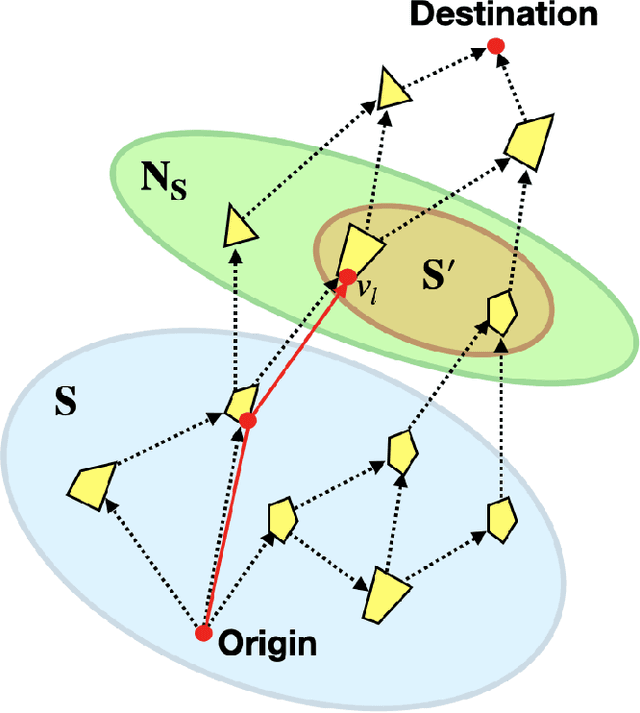
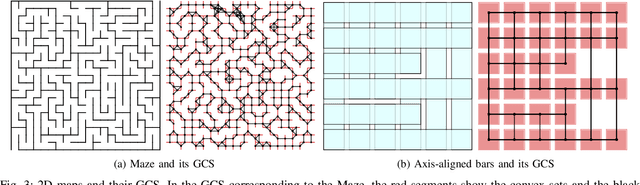
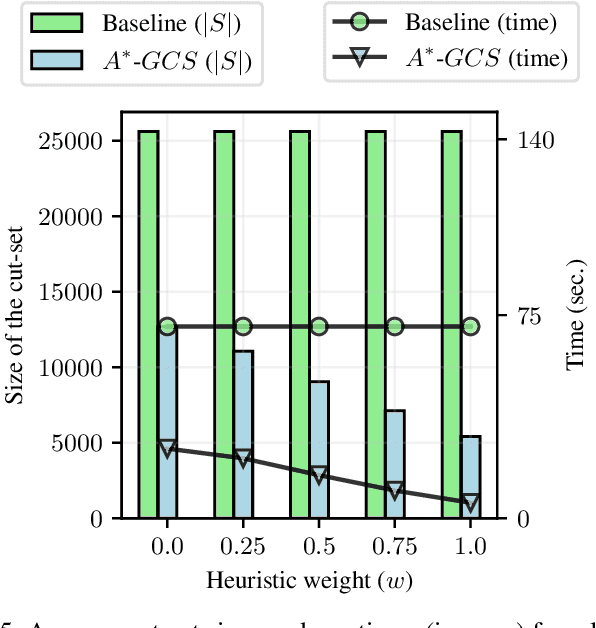
We present a novel algorithm that fuses the existing convex-programming based approach with heuristic information to find optimality guarantees and near-optimal paths for the Shortest Path Problem in the Graph of Convex Sets (SPP-GCS). Our method, inspired by $A^*$, initiates a best-first-like procedure from a designated subset of vertices and iteratively expands it until further growth is neither possible nor beneficial. Traditionally, obtaining solutions with bounds for an optimization problem involves solving a relaxation, modifying the relaxed solution to a feasible one, and then comparing the two solutions to establish bounds. However, for SPP-GCS, we demonstrate that reversing this process can be more advantageous, especially with Euclidean travel costs. In other words, we initially employ $A^*$ to find a feasible solution for SPP-GCS, then solve a convex relaxation restricted to the vertices explored by $A^*$ to obtain a relaxed solution, and finally, compare the solutions to derive bounds. We present numerical results to highlight the advantages of our algorithm over the existing approach in terms of the sizes of the convex programs solved and computation time.

A Mixed-Integer Conic Program for the Moving-Target Traveling Salesman Problem based on a Graph of Convex Sets

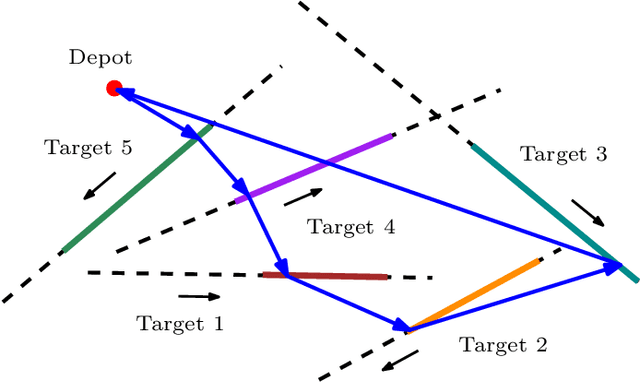
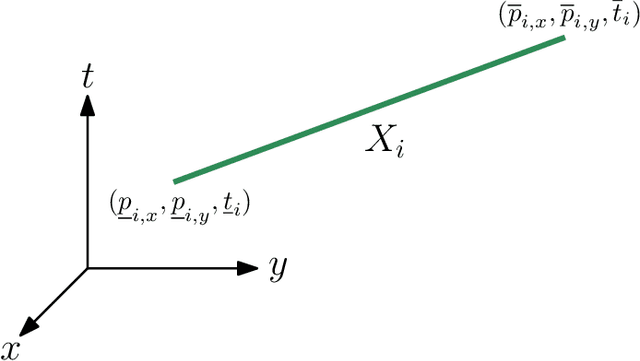
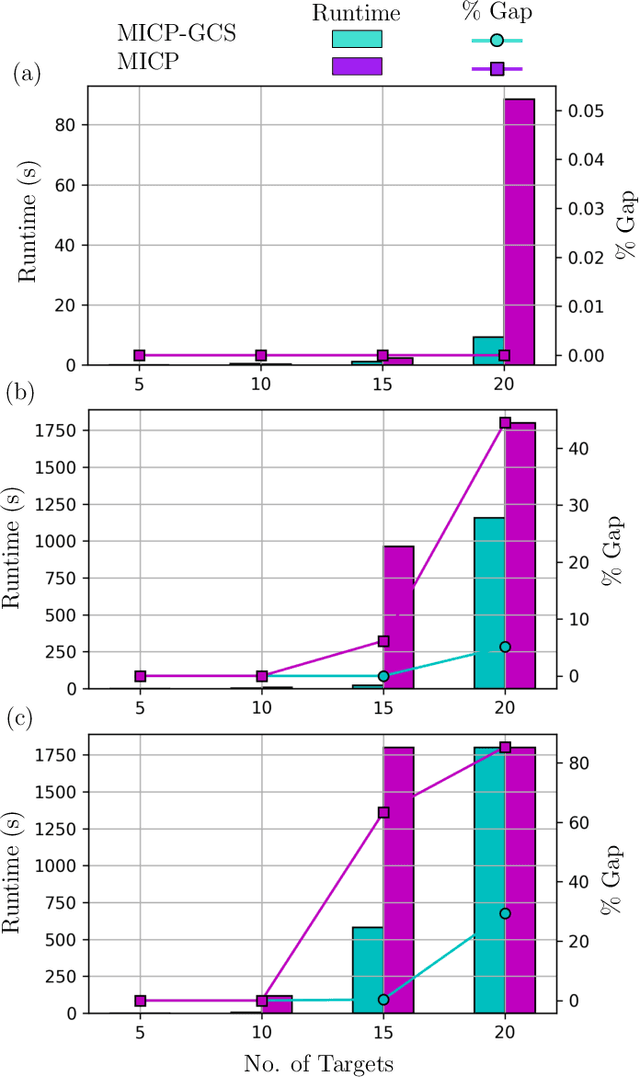
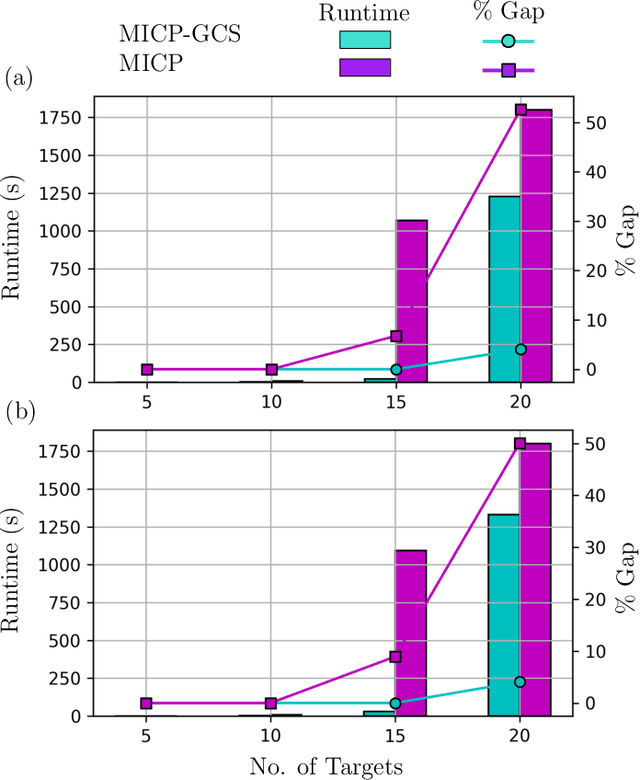
This paper introduces a new formulation that finds the optimum for the Moving-Target Traveling Salesman Problem (MT-TSP), which seeks to find a shortest path for an agent, that starts at a depot, visits a set of moving targets exactly once within their assigned time-windows, and returns to the depot. The formulation relies on the key idea that when the targets move along lines, their trajectories become convex sets within the space-time coordinate system. The problem then reduces to finding the shortest path within a graph of convex sets, subject to some speed constraints. We compare our formulation with the current state-of-the-art Mixed Integer Conic Program (MICP) solver for the MT-TSP. The experimental results show that our formulation outperforms the MICP for instances with up to 20 targets, with up to two orders of magnitude reduction in runtime, and up to a 60\% tighter optimality gap. We also show that the solution cost from the convex relaxation of our formulation provides significantly tighter lower bounds for the MT-TSP than the ones from the MICP.