A Mixed-Integer Conic Program for the Multi-Agent Moving-Target Traveling Salesman Problem

The Moving-Target Traveling Salesman Problem (MT-TSP) aims to find a shortest path for an agent that starts at a stationary depot, visits a set of moving targets exactly once, each within one of their respective time windows, and then returns to the depot. In this paper, we introduce a new Mixed-Integer Conic Program (MICP) formulation that finds the optimum for the Multi-Agent Moving-Target Traveling Salesman Problem (MA-MT-TSP), a generalization of the MT-TSP involving multiple agents. We obtain our formulation by first restating the current state-of-the-art MICP formulation for MA-MT-TSP as a Mixed-Integer Nonlinear Nonconvex Program, and then reformulating it as a new MICP. We present computational results to demonstrate the performance of our approach. The results show that our formulation significantly outperforms the state-of-the-art, with up to a two-order-of-magnitude reduction in runtime, and up to over 90% tighter optimality gap.

A Mixed-Integer Conic Program for the Moving-Target Traveling Salesman Problem based on a Graph of Convex Sets

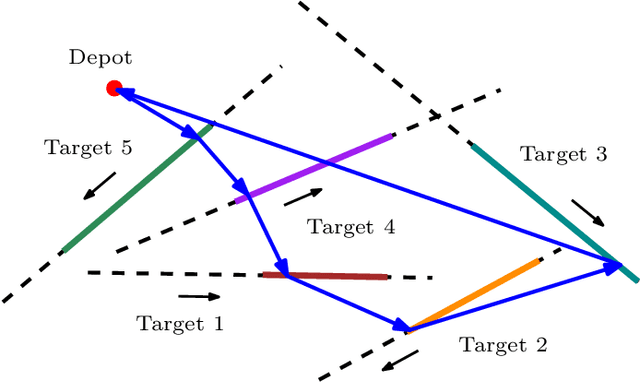
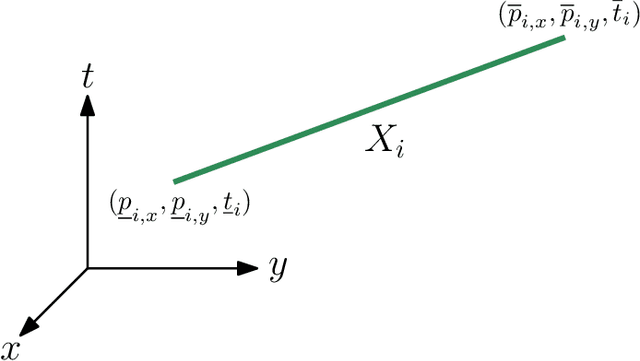
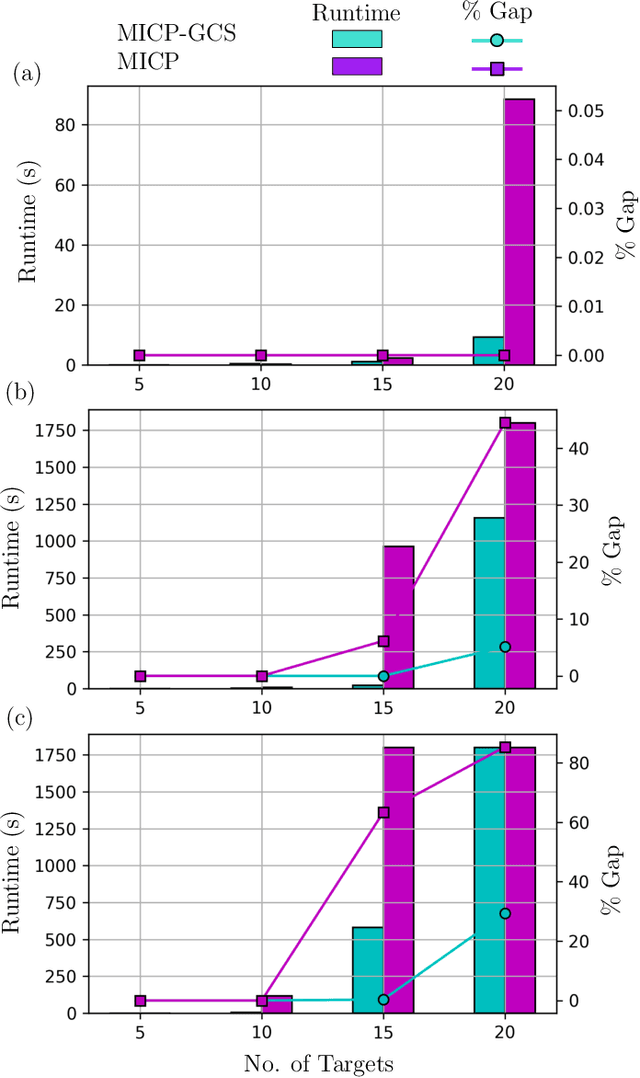
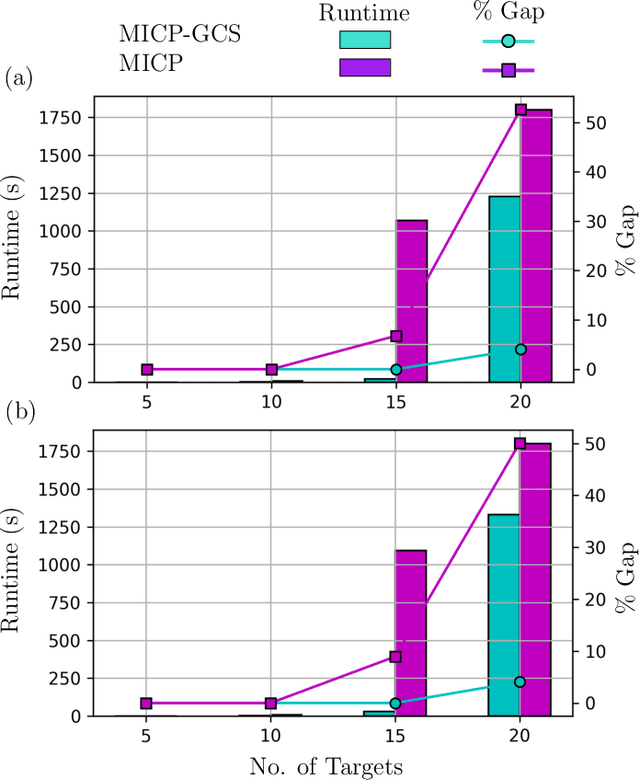
This paper introduces a new formulation that finds the optimum for the Moving-Target Traveling Salesman Problem (MT-TSP), which seeks to find a shortest path for an agent, that starts at a depot, visits a set of moving targets exactly once within their assigned time-windows, and returns to the depot. The formulation relies on the key idea that when the targets move along lines, their trajectories become convex sets within the space-time coordinate system. The problem then reduces to finding the shortest path within a graph of convex sets, subject to some speed constraints. We compare our formulation with the current state-of-the-art Mixed Integer Conic Program (MICP) solver for the MT-TSP. The experimental results show that our formulation outperforms the MICP for instances with up to 20 targets, with up to two orders of magnitude reduction in runtime, and up to a 60\% tighter optimality gap. We also show that the solution cost from the convex relaxation of our formulation provides significantly tighter lower bounds for the MT-TSP than the ones from the MICP.

C*: A New Bounding Approach for the Moving-Target Traveling Salesman Problem

We introduce a new bounding approach called Continuity* (C*) that provides optimality guarantees to the Moving-Target Traveling Salesman Problem (MT-TSP). Our approach relies on relaxing the continuity constraints on the agent's tour. This is done by partitioning the targets' trajectories into small sub-segments and allowing the agent to arrive at any point in one of the sub-segments and depart from any point in the same sub-segment when visiting each target. This lets us pose the bounding problem as a Generalized Traveling Salesman Problem (GTSP) in a graph where the cost of traveling an edge requires us to solve a new problem called the Shortest Feasible Travel (SFT). We also introduce C*-lite, which follows the same approach as C*, but uses simple and easy to compute lower-bounds to the SFT. We first prove that the proposed algorithms provide lower bounds to the MT-TSP. We also provide computational results to corroborate the performance of C* and C*-lite for instances with up to 15 targets. For the special case where targets travel along lines, we compare our C* variants with the SOCP based method, which is the current state-of-the-art solver for MT-TSP. While the SOCP based method performs well for instances with 5 and 10 targets, C* outperforms the SOCP based method for instances with 15 targets. For the general case, on average, our approaches find feasible solutions within ~4% of the lower bounds for the tested instances.