A Mixed-Integer Conic Program for the Moving-Target Traveling Salesman Problem based on a Graph of Convex Sets
Paper and Code
Mar 11, 2024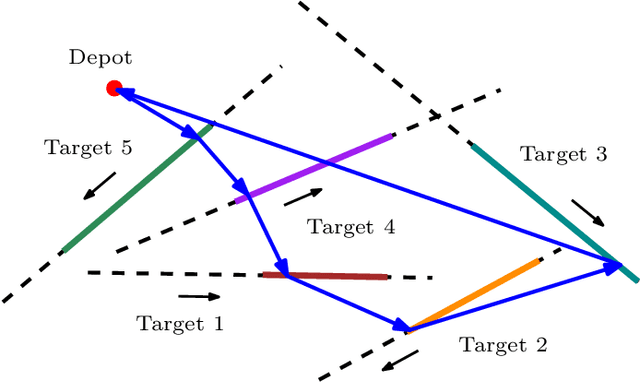
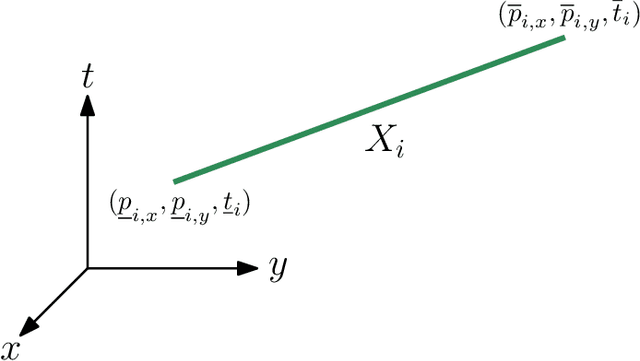
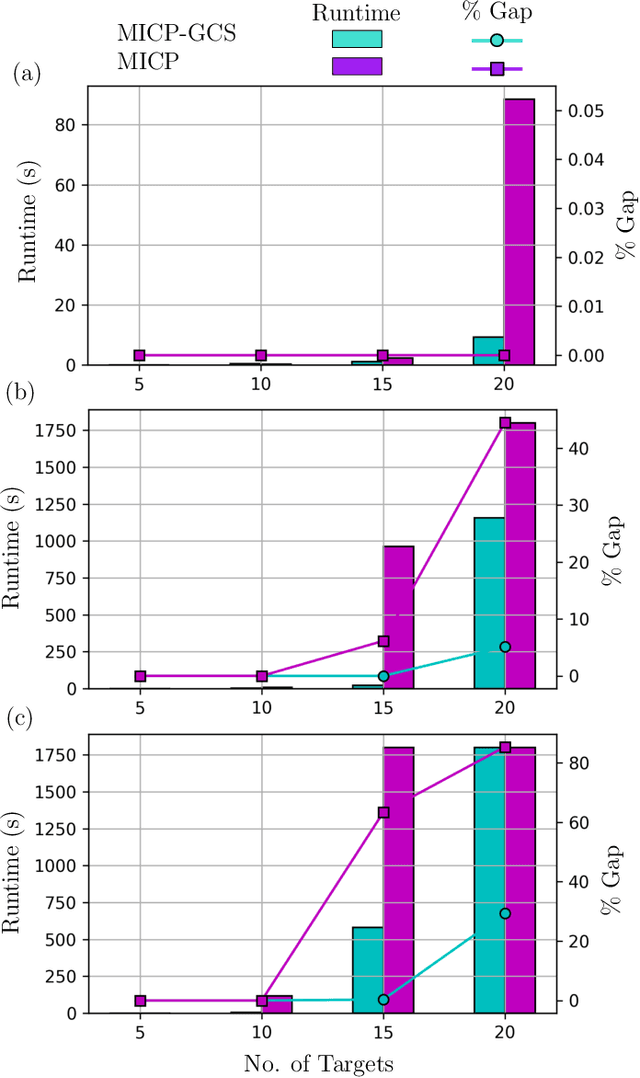
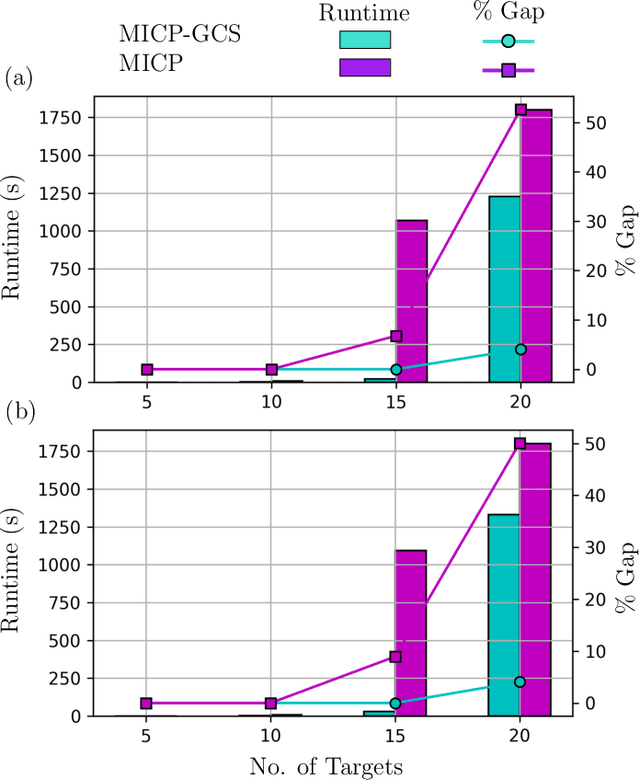
This paper introduces a new formulation that finds the optimum for the Moving-Target Traveling Salesman Problem (MT-TSP), which seeks to find a shortest path for an agent, that starts at a depot, visits a set of moving targets exactly once within their assigned time-windows, and returns to the depot. The formulation relies on the key idea that when the targets move along lines, their trajectories become convex sets within the space-time coordinate system. The problem then reduces to finding the shortest path within a graph of convex sets, subject to some speed constraints. We compare our formulation with the current state-of-the-art Mixed Integer Conic Program (MICP) solver for the MT-TSP. The experimental results show that our formulation outperforms the MICP for instances with up to 20 targets, with up to two orders of magnitude reduction in runtime, and up to a 60\% tighter optimality gap. We also show that the solution cost from the convex relaxation of our formulation provides significantly tighter lower bounds for the MT-TSP than the ones from the MICP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge