Ergodic Trajectory Planning with Dynamic Sensor Footprints

This paper addresses the problem of trajectory planning for information gathering with a dynamic and resolution-varying sensor footprint. Ergodic planning offers a principled framework that balances exploration (visiting all areas) and exploitation (focusing on high-information regions) by planning trajectories such that the time spent in a region is proportional to the amount of information in that region. Existing ergodic planning often oversimplifies the sensing model by assuming a point sensor or a footprint with constant shape and resolution. In practice, the sensor footprint can drastically change over time as the robot moves, such as aerial robots equipped with downward-facing cameras, whose field of view depends on the orientation and altitude. To overcome this limitation, we propose a new metric that accounts for dynamic sensor footprints, analyze the theoretic local optimality conditions, and propose numerical trajectory optimization algorithms. Experimental results show that the proposed approach can simultaneously optimize both the trajectories and sensor footprints, with up to an order of magnitude better ergodicity than conventional methods. We also deploy our approach in a multi-drone system to ergodically cover an object in 3D space.

Parallel, Asymptotically Optimal Algorithms for Moving Target Traveling Salesman Problems

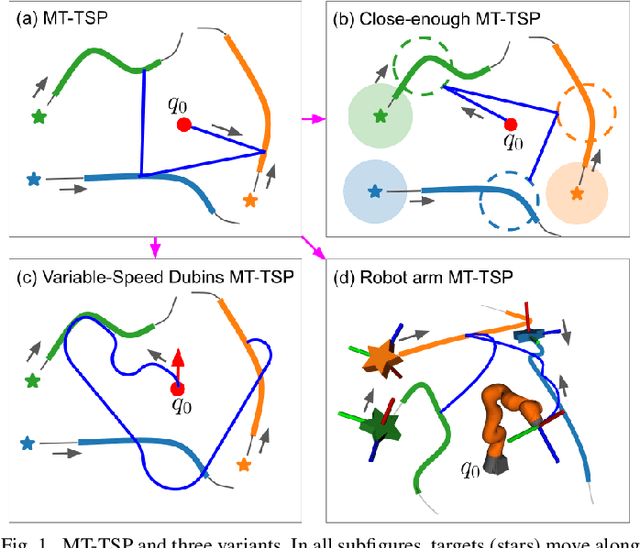
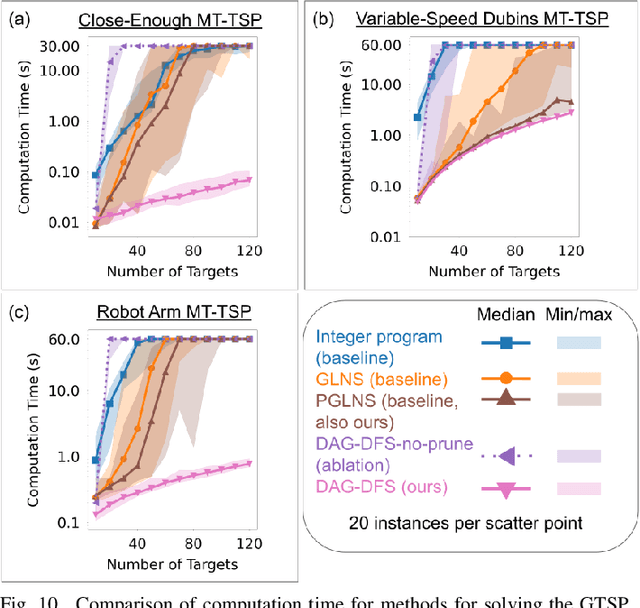
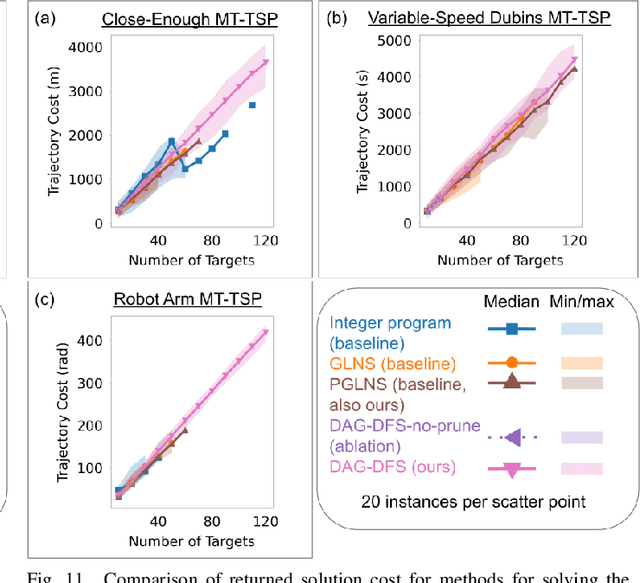
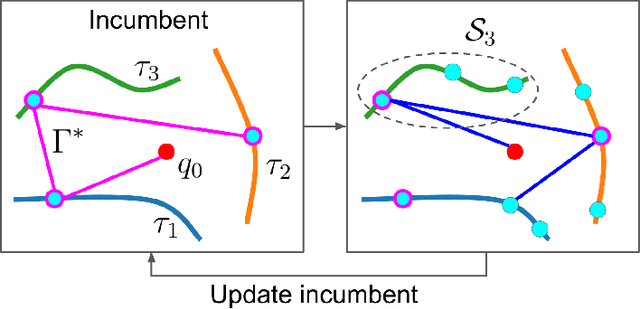
The Moving Target Traveling Salesman Problem (MT-TSP) seeks an agent trajectory that intercepts several moving targets, within a particular time window for each target. In the presence of generic nonlinear target trajectories or kinematic constraints on the agent, no prior algorithm guarantees convergence to an optimal MT-TSP solution. Therefore, we introduce the Iterated Random Generalized (IRG) TSP framework. The key idea behind IRG is to alternate between randomly sampling a set of agent configuration-time points, corresponding to interceptions of targets, and finding a sequence of interception points by solving a generalized TSP (GTSP). This alternation enables asymptotic convergence to the optimum. We introduce two parallel algorithms within the IRG framework. The first algorithm, IRG-PGLNS, solves GTSPs using PGLNS, our parallelized extension of the state-of-the-art solver GLNS. The second algorithm, Parallel Communicating GTSPs (PCG), solves GTSPs corresponding to several sets of points simultaneously. We present numerical results for three variants of the MT-TSP: one where intercepting a target only requires coming within a particular distance, another where the agent is a variable-speed Dubins car, and a third where the agent is a redundant robot arm. We show that IRG-PGLNS and PCG both converge faster than a baseline based on prior work.

A Complete and Bounded-Suboptimal Algorithm for a Moving Target Traveling Salesman Problem with Obstacles in 3D

The moving target traveling salesman problem with obstacles (MT-TSP-O) seeks an obstacle-free trajectory for an agent that intercepts a given set of moving targets, each within specified time windows, and returns to the agent's starting position. Each target moves with a constant velocity within its time windows, and the agent has a speed limit no smaller than any target's speed. We present FMC*-TSP, the first complete and bounded-suboptimal algorithm for the MT-TSP-O, and results for an agent whose configuration space is $\mathbb{R}^3$. Our algorithm interleaves a high-level search and a low-level search, where the high-level search solves a generalized traveling salesman problem with time windows (GTSP-TW) to find a sequence of targets and corresponding time windows for the agent to visit. Given such a sequence, the low-level search then finds an associated agent trajectory. To solve the low-level planning problem, we develop a new algorithm called FMC*, which finds a shortest path on a graph of convex sets (GCS) via implicit graph search and pruning techniques specialized for problems with moving targets. We test FMC*-TSP on 280 problem instances with up to 40 targets and demonstrate its smaller median runtime than a baseline based on prior work.

A Mixed-Integer Conic Program for the Multi-Agent Moving-Target Traveling Salesman Problem

The Moving-Target Traveling Salesman Problem (MT-TSP) aims to find a shortest path for an agent that starts at a stationary depot, visits a set of moving targets exactly once, each within one of their respective time windows, and then returns to the depot. In this paper, we introduce a new Mixed-Integer Conic Program (MICP) formulation that finds the optimum for the Multi-Agent Moving-Target Traveling Salesman Problem (MA-MT-TSP), a generalization of the MT-TSP involving multiple agents. We obtain our formulation by first restating the current state-of-the-art MICP formulation for MA-MT-TSP as a Mixed-Integer Nonlinear Nonconvex Program, and then reformulating it as a new MICP. We present computational results to demonstrate the performance of our approach. The results show that our formulation significantly outperforms the state-of-the-art, with up to a two-order-of-magnitude reduction in runtime, and up to over 90% tighter optimality gap.

Loosely Synchronized Rule-Based Planning for Multi-Agent Path Finding with Asynchronous Actions

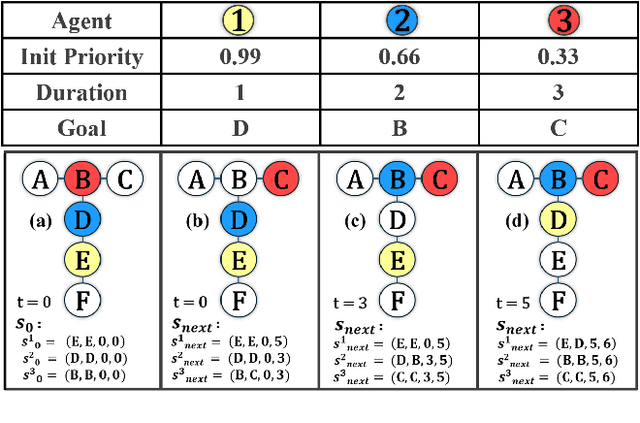
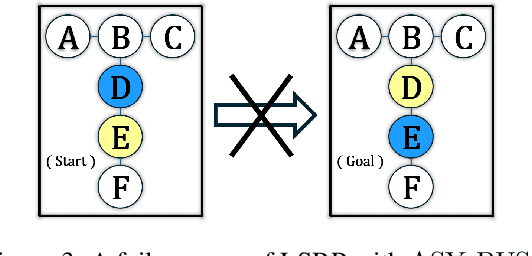
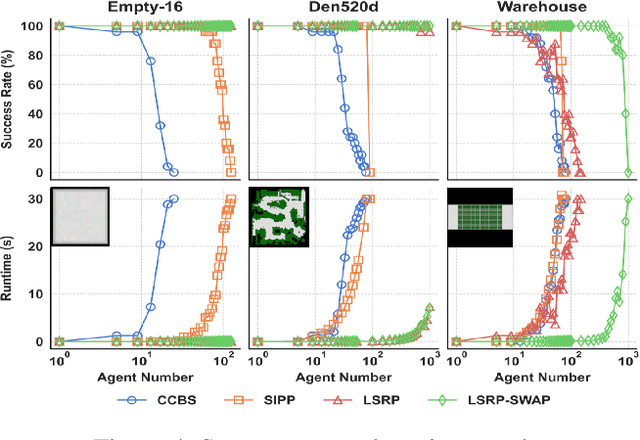
Multi-Agent Path Finding (MAPF) seeks collision-free paths for multiple agents from their respective starting locations to their respective goal locations while minimizing path costs. Although many MAPF algorithms were developed and can handle up to thousands of agents, they usually rely on the assumption that each action of the agent takes a time unit, and the actions of all agents are synchronized in a sense that the actions of agents start at the same discrete time step, which may limit their use in practice. Only a few algorithms were developed to address asynchronous actions, and they all lie on one end of the spectrum, focusing on finding optimal solutions with limited scalability. This paper develops new planners that lie on the other end of the spectrum, trading off solution quality for scalability, by finding an unbounded sub-optimal solution for many agents. Our method leverages both search methods (LSS) in handling asynchronous actions and rule-based planning methods (PIBT) for MAPF. We analyze the properties of our method and test it against several baselines with up to 1000 agents in various maps. Given a runtime limit, our method can handle an order of magnitude more agents than the baselines with about 25% longer makespan.

Search-Based Path Planning among Movable Obstacles

This paper investigates Path planning Among Movable Obstacles (PAMO), which seeks a minimum cost collision-free path among static obstacles from start to goal while allowing the robot to push away movable obstacles (i.e., objects) along its path when needed. To develop planners that are complete and optimal for PAMO, the planner has to search a giant state space involving both the location of the robot as well as the locations of the objects, which grows exponentially with respect to the number of objects. The main idea in this paper is that, only a small fraction of this giant state space needs to be explored during planning as guided by a heuristic, and most of the objects far away from the robot are intact, which thus leads to runtime efficient algorithms. Based on this idea, this paper introduces two PAMO formulations, i.e., bi-objective and resource constrained problems in an occupancy grid, and develops PAMO*, a search method with completeness and solution optimality guarantees, to solve the two problems. We then further extend PAMO* to hybrid-state PAMO* to plan in continuous spaces with high-fidelity interaction between the robot and the objects. Our results show that, PAMO* can often find optimal solutions within a second in cluttered environments with up to 400 objects.

A Complete Algorithm for a Moving Target Traveling Salesman Problem with Obstacles

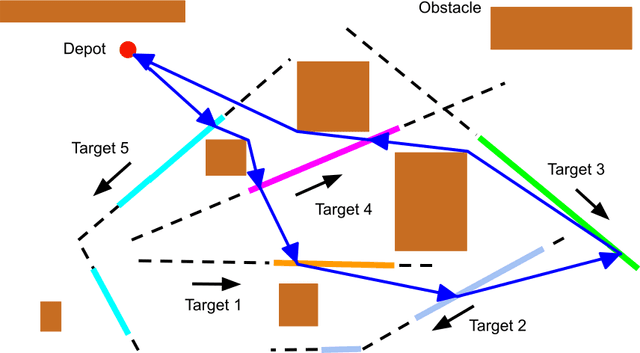
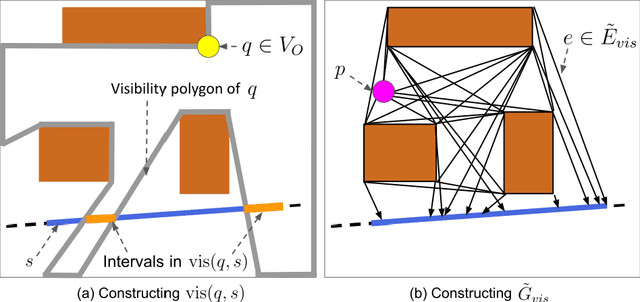
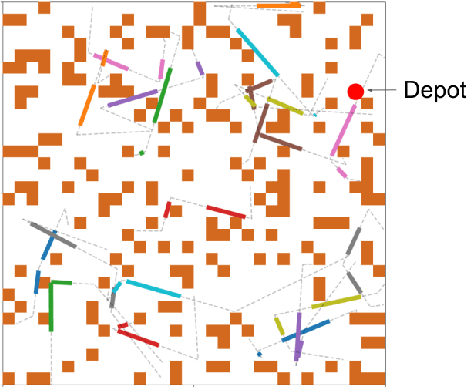
The moving target traveling salesman problem with obstacles (MT-TSP-O) is a generalization of the traveling salesman problem (TSP) where, as its name suggests, the targets are moving. A solution to the MT-TSP-O is a trajectory that visits each moving target during a certain time window(s), and this trajectory avoids stationary obstacles. We assume each target moves at a constant velocity during each of its time windows. The agent has a speed limit, and this speed limit is no smaller than any target's speed. This paper presents the first complete algorithm for finding feasible solutions to the MT-TSP-O. Our algorithm builds a tree where the nodes are agent trajectories intercepting a unique sequence of targets within a unique sequence of time windows. We generate each of a parent node's children by extending the parent's trajectory to intercept one additional target, each child corresponding to a different choice of target and time window. This extension consists of planning a trajectory from the parent trajectory's final point in space-time to a moving target. To solve this point-to-moving-target subproblem, we define a novel generalization of a visibility graph called a moving target visibility graph (MTVG). Our overall algorithm is called MTVG-TSP. To validate MTVG-TSP, we test it on 570 instances with up to 30 targets. We implement a baseline method that samples trajectories of targets into points, based on prior work on special cases of the MT-TSP-O. MTVG-TSP finds feasible solutions in all cases where the baseline does, and when the sum of the targets' time window lengths enters a critical range, MTVG-TSP finds a feasible solution with up to 38 times less computation time.

PWTO: A Heuristic Approach for Trajectory Optimization in Complex Terrains

This paper considers a trajectory planning problem for a robot navigating complex terrains, which arises in applications ranging from autonomous mining vehicles to planetary rovers. The problem seeks to find a low-cost dynamically feasible trajectory for the robot. The problem is challenging as it requires solving a non-linear optimization problem that often has many local minima due to the complex terrain. To address the challenge, we propose a method called Pareto-optimal Warm-started Trajectory Optimization (PWTO) that attempts to combine the benefits of graph search and trajectory optimization, two very different approaches to planning. PWTO first creates a state lattice using simplified dynamics of the robot and leverages a multi-objective graph search method to obtain a set of paths. Each of the paths is then used to warm-start a local trajectory optimization process, so that different local minima are explored to find a globally low-cost solution. In our tests, the solution cost computed by PWTO is often less than half of the costs computed by the baselines. In addition, we verify the trajectories generated by PWTO in Gazebo simulation in complex terrains with both wheeled and quadruped robots. The code of this paper is open sourced and can be found at https://github.com/rap-lab-org/public_pwto.

Imperative Learning: A Self-supervised Neural-Symbolic Learning Framework for Robot Autonomy

Data-driven methods such as reinforcement and imitation learning have achieved remarkable success in robot autonomy. However, their data-centric nature still hinders them from generalizing well to ever-changing environments. Moreover, collecting large datasets for robotic tasks is often impractical and expensive. To overcome these challenges, we introduce a new self-supervised neural-symbolic (NeSy) computational framework, imperative learning (IL), for robot autonomy, leveraging the generalization abilities of symbolic reasoning. The framework of IL consists of three primary components: a neural module, a reasoning engine, and a memory system. We formulate IL as a special bilevel optimization (BLO), which enables reciprocal learning over the three modules. This overcomes the label-intensive obstacles associated with data-driven approaches and takes advantage of symbolic reasoning concerning logical reasoning, physical principles, geometric analysis, etc. We discuss several optimization techniques for IL and verify their effectiveness in five distinct robot autonomy tasks including path planning, rule induction, optimal control, visual odometry, and multi-robot routing. Through various experiments, we show that IL can significantly enhance robot autonomy capabilities and we anticipate that it will catalyze further research across diverse domains.

Propagative Distance Optimization for Constrained Inverse Kinematics

This paper investigates a constrained inverse kinematic (IK) problem that seeks a feasible configuration of an articulated robot under various constraints such as joint limits and obstacle collision avoidance. Due to the high-dimensionality and complex constraints, this problem is often solved numerically via iterative local optimization. Classic local optimization methods take joint angles as the decision variable, which suffers from non-linearity caused by the trigonometric constraints. Recently, distance-based IK methods have been developed as an alternative approach that formulates IK as an optimization over the distances among points attached to the robot and the obstacles. Although distance-based methods have demonstrated unique advantages, they still suffer from low computational efficiency, since these approaches usually ignore the chain structure in the kinematics of serial robots. This paper proposes a new method called propagative distance optimization for constrained inverse kinematics (PDO-IK), which captures and leverages the chain structure in the distance-based formulation and expedites the optimization by computing forward kinematics and the Jacobian propagatively along the kinematic chain. Test results show that PDO-IK runs up to two orders of magnitude faster than the existing distance-based methods under joint limits constraints and obstacle avoidance constraints. It also achieves up to three times higher success rates than the conventional joint-angle-based optimization methods for IK problems. The high runtime efficiency of PDO-IK allows the real-time computation (10$-$1500 Hz) and enables a simulated humanoid robot with 19 degrees of freedom (DoFs) to avoid moving obstacles, which is otherwise hard to achieve with the baselines.