Loosely Synchronized Rule-Based Planning for Multi-Agent Path Finding with Asynchronous Actions

Multi-Agent Path Finding (MAPF) seeks collision-free paths for multiple agents from their respective starting locations to their respective goal locations while minimizing path costs. Although many MAPF algorithms were developed and can handle up to thousands of agents, they usually rely on the assumption that each action of the agent takes a time unit, and the actions of all agents are synchronized in a sense that the actions of agents start at the same discrete time step, which may limit their use in practice. Only a few algorithms were developed to address asynchronous actions, and they all lie on one end of the spectrum, focusing on finding optimal solutions with limited scalability. This paper develops new planners that lie on the other end of the spectrum, trading off solution quality for scalability, by finding an unbounded sub-optimal solution for many agents. Our method leverages both search methods (LSS) in handling asynchronous actions and rule-based planning methods (PIBT) for MAPF. We analyze the properties of our method and test it against several baselines with up to 1000 agents in various maps. Given a runtime limit, our method can handle an order of magnitude more agents than the baselines with about 25% longer makespan.

Reducing Redundant Work in Jump Point Search

JPS (Jump Point Search) is a state-of-the-art optimal algorithm for online grid-based pathfinding. Widely used in games and other navigation scenarios, JPS nevertheless can exhibit pathological behaviours which are not well studied: (i) it may repeatedly scan the same area of the map to find successors; (ii) it may generate and expand suboptimal search nodes. In this work, we examine the source of these pathological behaviours, show how they can occur in practice, and propose a purely online approach, called Constrained JPS (CJPS), to tackle them efficiently. Experimental results show that CJPS has low overheads and is often faster than JPS in dynamically changing grid environments: by up to 7x in large game maps and up to 14x in pathological scenarios.

Faster and More Robust Mesh-based Algorithms for Obstacle k-Nearest Neighbour

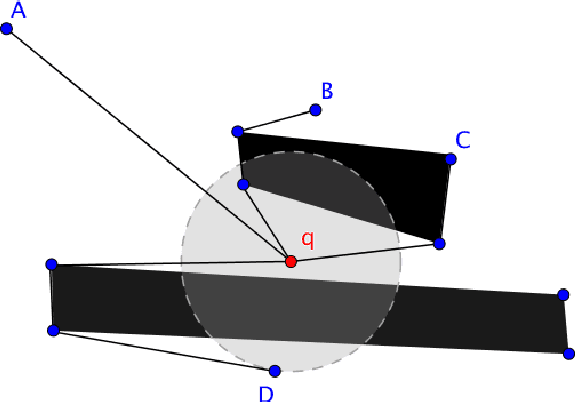
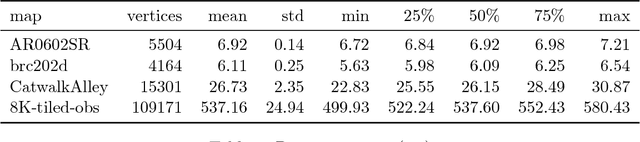
We are interested in the problem of finding $k$ nearest neighbours in the plane and in the presence of polygonal obstacles ($\textit{OkNN}$). Widely used algorithms for OkNN are based on incremental visibility graphs, which means they require costly and online visibility checking and have worst-case quadratic running time. Recently $\mathbf{Polyanya}$, a fast point-to-point pathfinding algorithm was proposed which avoids the disadvantages of visibility graphs by searching over an alternative data structure known as a navigation mesh. Previously, we adapted $\mathbf{Polyanya}$ to multi-target scenarios by developing two specialised heuristic functions: the $\mathbf{Interval heuristic}$ $h_v$ and the $\mathbf{Target heuristic}$ $h_t$. Though these methods outperform visibility graph algorithms by orders of magnitude in all our experiments they are not robust: $h_v$ expands many redundant nodes when the set of neighbours is small while $h_t$ performs poorly when the set of neighbours is large. In this paper, we propose new algorithms and heuristics for OkNN which perform well regardless of neighbour density.