Faster and More Robust Mesh-based Algorithms for Obstacle k-Nearest Neighbour
Paper and Code
Aug 13, 2018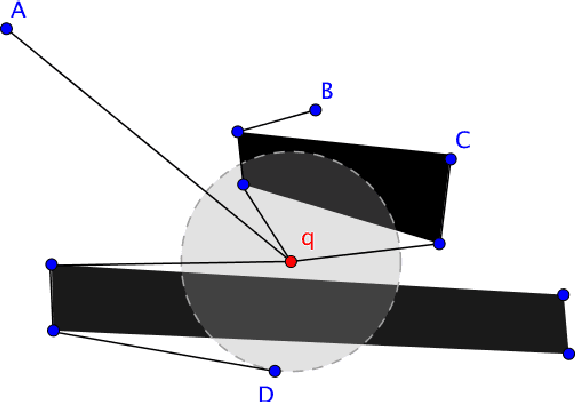

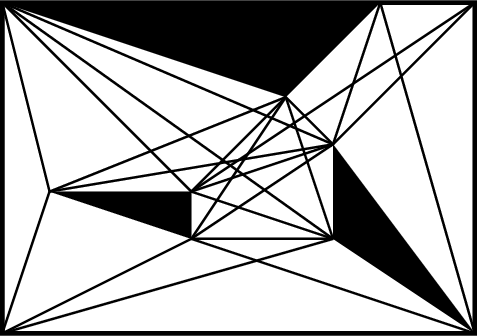
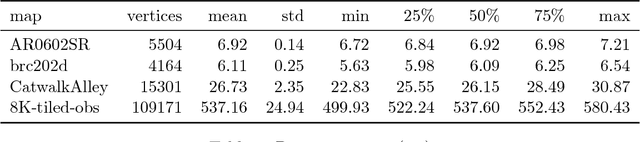
We are interested in the problem of finding $k$ nearest neighbours in the plane and in the presence of polygonal obstacles ($\textit{OkNN}$). Widely used algorithms for OkNN are based on incremental visibility graphs, which means they require costly and online visibility checking and have worst-case quadratic running time. Recently $\mathbf{Polyanya}$, a fast point-to-point pathfinding algorithm was proposed which avoids the disadvantages of visibility graphs by searching over an alternative data structure known as a navigation mesh. Previously, we adapted $\mathbf{Polyanya}$ to multi-target scenarios by developing two specialised heuristic functions: the $\mathbf{Interval heuristic}$ $h_v$ and the $\mathbf{Target heuristic}$ $h_t$. Though these methods outperform visibility graph algorithms by orders of magnitude in all our experiments they are not robust: $h_v$ expands many redundant nodes when the set of neighbours is small while $h_t$ performs poorly when the set of neighbours is large. In this paper, we propose new algorithms and heuristics for OkNN which perform well regardless of neighbour density.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge