Tracking Progress in Multi-Agent Path Finding

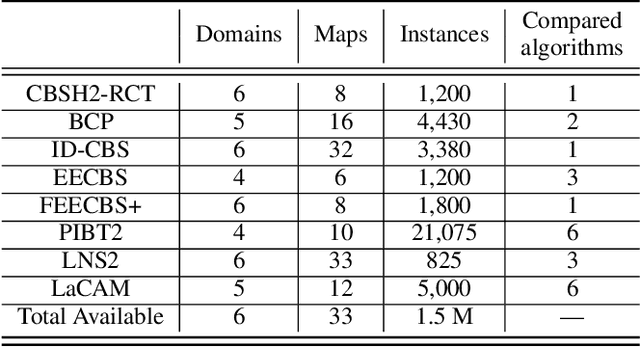
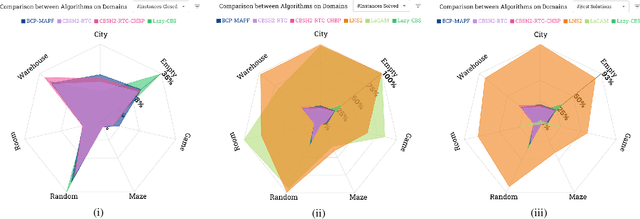
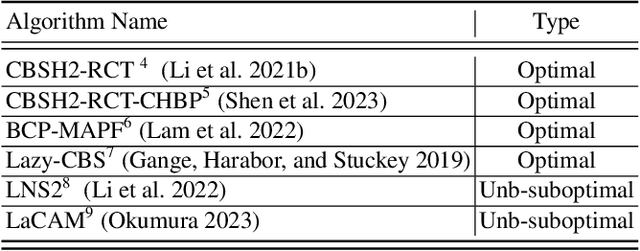
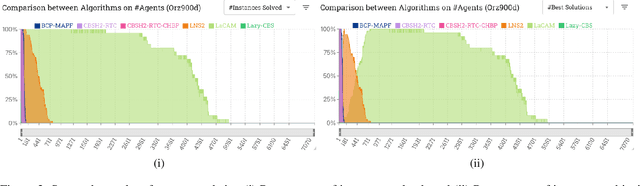
Multi-Agent Path Finding (MAPF) is an important core problem for many new and emerging industrial applications. Many works appear on this topic each year, and a large number of substantial advancements and performance improvements have been reported. Yet measuring overall progress in MAPF is difficult: there are many potential competitors, and the computational burden for comprehensive experimentation is prohibitively large. Moreover, detailed data from past experimentation is usually unavailable. In this work, we introduce a set of methodological and visualisation tools which can help the community establish clear indicators for state-of-the-art MAPF performance and which can facilitate large-scale comparisons between MAPF solvers. Our objectives are to lower the barrier of entry for new researchers and to further promote the study of MAPF, since progress in the area and the main challenges are made much clearer.

Integrated Task Assignment and Path Planning for Capacitated Multi-Agent Pickup and Delivery

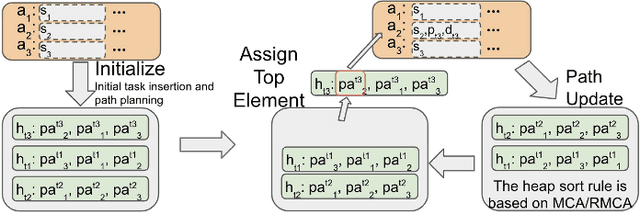
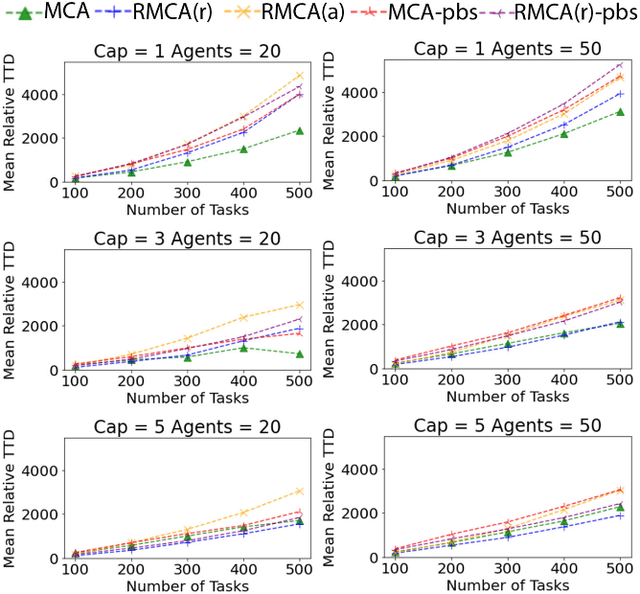
Multi-agent Pickup and Delivery (MAPD) is a challenging industrial problem where a team of robots is tasked with transporting a set of tasks, each from an initial location and each to a specified target location. Appearing in the context of automated warehouse logistics and automated mail sortation, MAPD requires first deciding which robot is assigned what task (i.e., Task Assignment or TA) followed by a subsequent coordination problem where each robot must be assigned collision-free paths so as to successfully complete its assignment (i.e., Multi-Agent Path Finding or MAPF). Leading methods in this area solve MAPD sequentially: first assigning tasks, then assigning paths. In this work we propose a new coupled method where task assignment choices are informed by actual delivery costs instead of by lower-bound estimates. The main ingredients of our approach are a marginal-cost assignment heuristic and a meta-heuristic improvement strategy based on Large Neighbourhood Search. As a further contribution, we also consider a variant of the MAPD problem where each robot can carry multiple tasks instead of just one. Numerical simulations show that our approach yields efficient and timely solutions and we report significant improvement compared with other recent methods from the literature.

Faster and More Robust Mesh-based Algorithms for Obstacle k-Nearest Neighbour

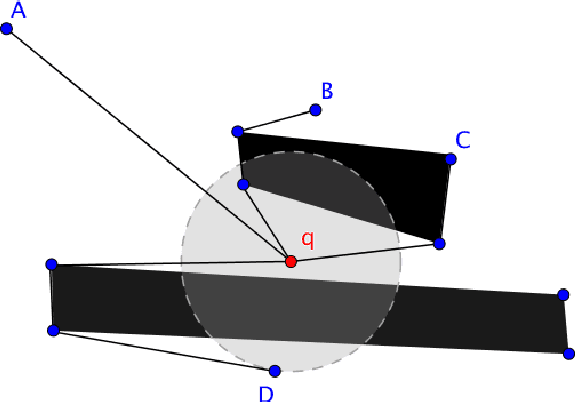
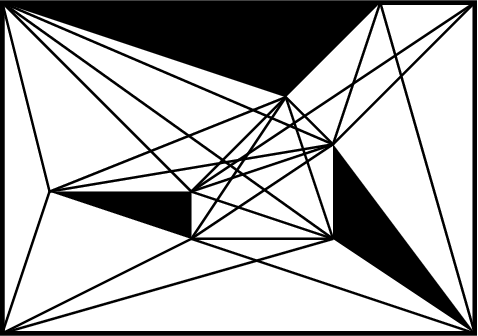
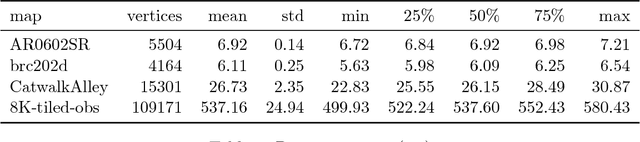
We are interested in the problem of finding $k$ nearest neighbours in the plane and in the presence of polygonal obstacles ($\textit{OkNN}$). Widely used algorithms for OkNN are based on incremental visibility graphs, which means they require costly and online visibility checking and have worst-case quadratic running time. Recently $\mathbf{Polyanya}$, a fast point-to-point pathfinding algorithm was proposed which avoids the disadvantages of visibility graphs by searching over an alternative data structure known as a navigation mesh. Previously, we adapted $\mathbf{Polyanya}$ to multi-target scenarios by developing two specialised heuristic functions: the $\mathbf{Interval heuristic}$ $h_v$ and the $\mathbf{Target heuristic}$ $h_t$. Though these methods outperform visibility graph algorithms by orders of magnitude in all our experiments they are not robust: $h_v$ expands many redundant nodes when the set of neighbours is small while $h_t$ performs poorly when the set of neighbours is large. In this paper, we propose new algorithms and heuristics for OkNN which perform well regardless of neighbour density.