SAMO: A Lightweight Sharpness-Aware Approach for Multi-Task Optimization with Joint Global-Local Perturbation

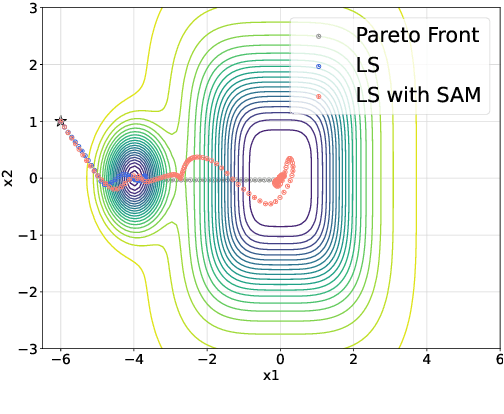
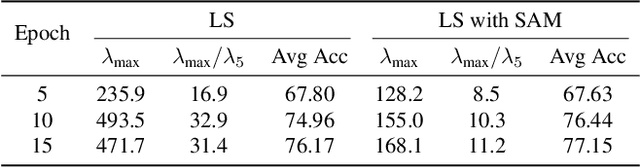
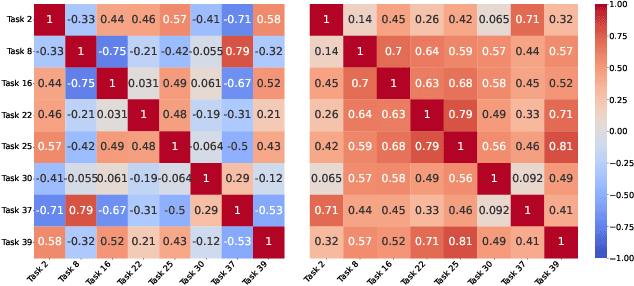
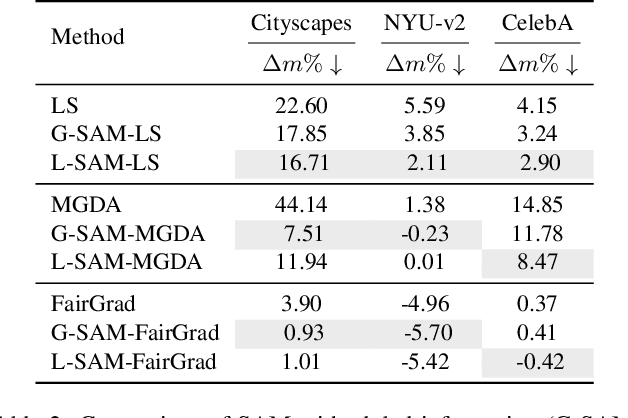
Multi-task learning (MTL) enables a joint model to capture commonalities across multiple tasks, reducing computation costs and improving data efficiency. However, a major challenge in MTL optimization is task conflicts, where the task gradients differ in direction or magnitude, limiting model performance compared to single-task counterparts. Sharpness-aware minimization (SAM) minimizes task loss while simultaneously reducing the sharpness of the loss landscape. Our empirical observations show that SAM effectively mitigates task conflicts in MTL. Motivated by these findings, we explore integrating SAM into MTL but face two key challenges. While both the average loss gradient and individual task gradients-referred to as global and local information-contribute to SAM, how to combine them remains unclear. Moreover, directly computing each task gradient introduces significant computational and memory overheads. To address these challenges, we propose SAMO, a lightweight \textbf{S}harpness-\textbf{A}ware \textbf{M}ulti-task \textbf{O}ptimization approach, that leverages a joint global-local perturbation. The local perturbations are approximated using only forward passes and are layerwise normalized to improve efficiency. Extensive experiments on a suite of multi-task benchmarks demonstrate both the effectiveness and efficiency of our method. Code is available at https://github.com/OptMN-Lab/SAMO.

Scalable Bilevel Loss Balancing for Multi-Task Learning

Multi-task learning (MTL) has been widely adopted for its ability to simultaneously learn multiple tasks. While existing gradient manipulation methods often yield more balanced solutions than simple scalarization-based approaches, they typically incur a significant computational overhead of $\mathcal{O}(K)$ in both time and memory, where $K$ is the number of tasks. In this paper, we propose BiLB4MTL, a simple and scalable loss balancing approach for MTL, formulated from a novel bilevel optimization perspective. Our method incorporates three key components: (i) an initial loss normalization, (ii) a bilevel loss-balancing formulation, and (iii) a scalable first-order algorithm that requires only $\mathcal{O}(1)$ time and memory. Theoretically, we prove that BiLB4MTL guarantees convergence not only to a stationary point of the bilevel loss balancing problem but also to an $\epsilon$-accurate Pareto stationary point for all $K$ loss functions under mild conditions. Extensive experiments on diverse multi-task datasets demonstrate that BiLB4MTL achieves state-of-the-art performance in both accuracy and efficiency. Code is available at https://github.com/OptMN-Lab/-BiLB4MTL.

ReGNet: Reciprocal Space-Aware Long-Range Modeling and Multi-Property Prediction for Crystals

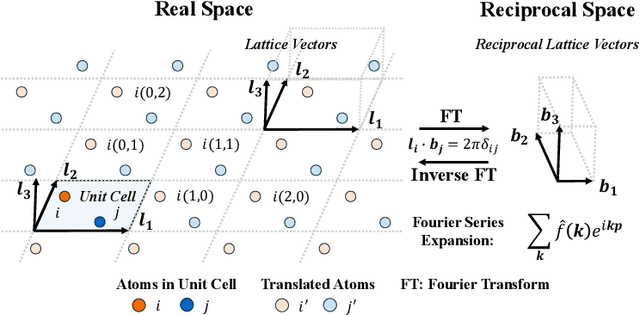
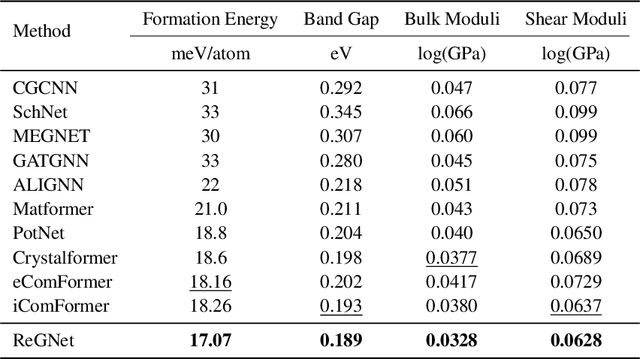
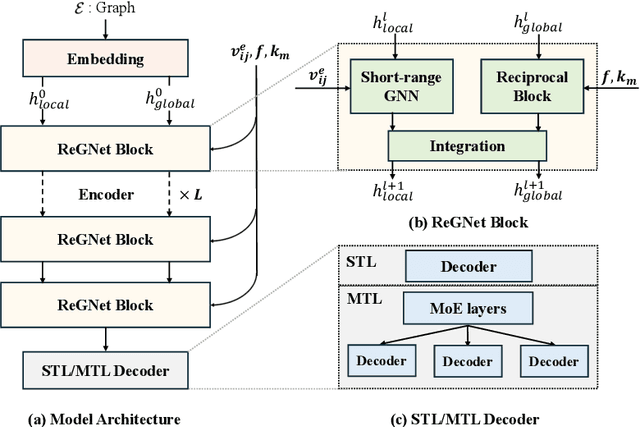
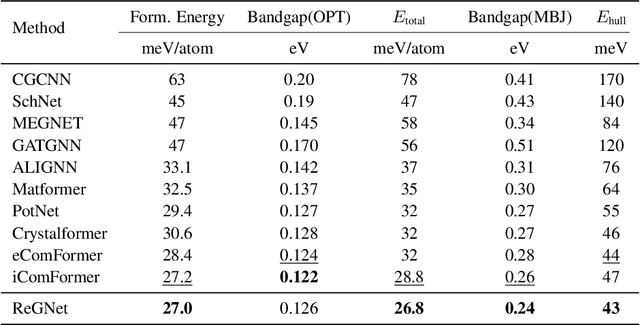
Predicting properties of crystals from their structures is a fundamental yet challenging task in materials science. Unlike molecules, crystal structures exhibit infinite periodic arrangements of atoms, requiring methods capable of capturing both local and global information effectively. However, most current works fall short of capturing long-range interactions within periodic structures. To address this limitation, we leverage reciprocal space to efficiently encode long-range interactions with learnable filters within Fourier transforms. We introduce Reciprocal Geometry Network (ReGNet), a novel architecture that integrates geometric GNNs and reciprocal blocks to model short-range and long-range interactions, respectively. Additionally, we introduce ReGNet-MT, a multi-task extension that employs mixture of experts (MoE) for multi-property prediction. Experimental results on the JARVIS and Materials Project benchmarks demonstrate that ReGNet achieves significant performance improvements. Moreover, ReGNet-MT attains state-of-the-art results on two bandgap properties due to positive transfer, while maintaining high computational efficiency. These findings highlight the potential of our model as a scalable and accurate solution for crystal property prediction. The code will be released upon paper acceptance.

Enhancing Diffusion Posterior Sampling for Inverse Problems by Integrating Crafted Measurements

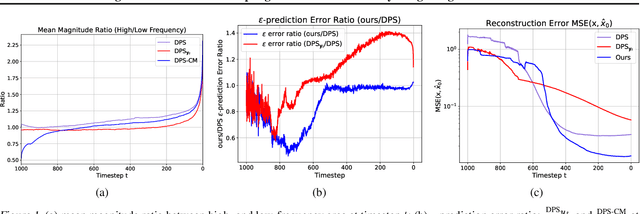
Diffusion models have emerged as a powerful foundation model for visual generation. With an appropriate sampling process, it can effectively serve as a generative prior to solve general inverse problems. Current posterior sampling based methods take the measurement (i.e., degraded image sample) into the posterior sampling to infer the distribution of the target data (i.e., clean image sample). However, in this manner, we show that high-frequency information can be prematurely introduced during the early stages, which could induce larger posterior estimate errors during the restoration sampling. To address this issue, we first reveal that forming the log posterior gradient with the noisy measurement ( i.e., samples from a diffusion forward process) instead of the clean one can benefit the reverse process. Consequently, we propose a novel diffusion posterior sampling method DPS-CM, which incorporates a Crafted Measurement (i.e., samples generated by a reverse denoising process, compared to random sampling with noise in standard methods) to form the posterior estimate. This integration aims to mitigate the misalignment with the diffusion prior caused by cumulative posterior estimate errors. Experimental results demonstrate that our approach significantly improves the overall capacity to solve general and noisy inverse problems, such as Gaussian deblurring, super-resolution, inpainting, nonlinear deblurring, and tasks with Poisson noise, relative to existing approaches.

Meta-Learning with Heterogeneous Tasks

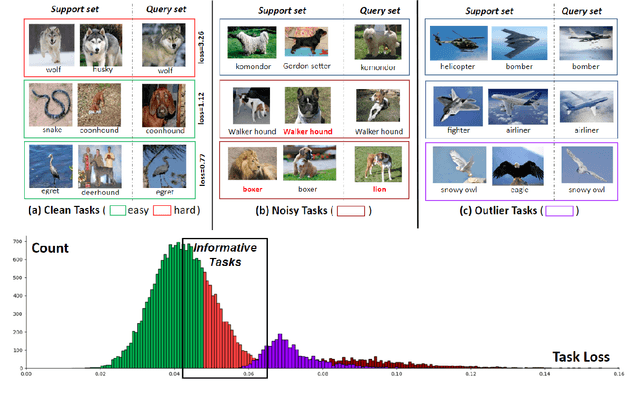
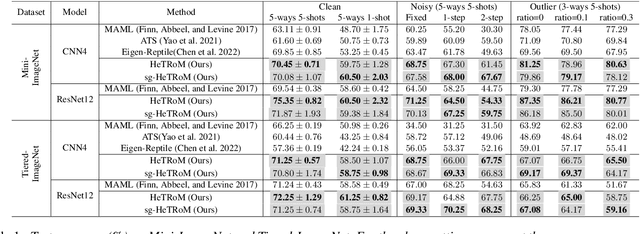
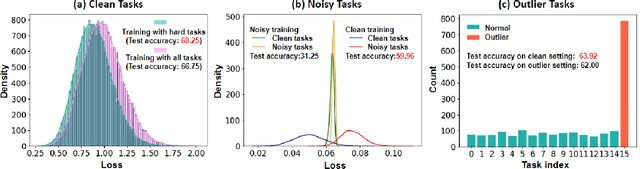
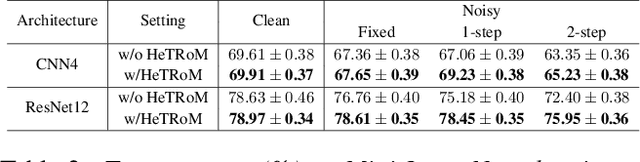
Meta-learning is a general approach to equip machine learning models with the ability to handle few-shot scenarios when dealing with many tasks. Most existing meta-learning methods work based on the assumption that all tasks are of equal importance. However, real-world applications often present heterogeneous tasks characterized by varying difficulty levels, noise in training samples, or being distinctively different from most other tasks. In this paper, we introduce a novel meta-learning method designed to effectively manage such heterogeneous tasks by employing rank-based task-level learning objectives, Heterogeneous Tasks Robust Meta-learning (HeTRoM). HeTRoM is proficient in handling heterogeneous tasks, and it prevents easy tasks from overwhelming the meta-learner. The approach allows for an efficient iterative optimization algorithm based on bi-level optimization, which is then improved by integrating statistical guidance. Our experimental results demonstrate that our method provides flexibility, enabling users to adapt to diverse task settings and enhancing the meta-learner's overall performance.

Tuning-Free Bilevel Optimization: New Algorithms and Convergence Analysis

Bilevel optimization has recently attracted considerable attention due to its abundant applications in machine learning problems. However, existing methods rely on prior knowledge of problem parameters to determine stepsizes, resulting in significant effort in tuning stepsizes when these parameters are unknown. In this paper, we propose two novel tuning-free algorithms, D-TFBO and S-TFBO. D-TFBO employs a double-loop structure with stepsizes adaptively adjusted by the "inverse of cumulative gradient norms" strategy. S-TFBO features a simpler fully single-loop structure that updates three variables simultaneously with a theory-motivated joint design of adaptive stepsizes for all variables. We provide a comprehensive convergence analysis for both algorithms and show that D-TFBO and S-TFBO respectively require $O(\frac{1}{\epsilon})$ and $O(\frac{1}{\epsilon}\log^4(\frac{1}{\epsilon}))$ iterations to find an $\epsilon$-accurate stationary point, (nearly) matching their well-tuned counterparts using the information of problem parameters. Experiments on various problems show that our methods achieve performance comparable to existing well-tuned approaches, while being more robust to the selection of initial stepsizes. To the best of our knowledge, our methods are the first to completely eliminate the need for stepsize tuning, while achieving theoretical guarantees.

Why Fine-Tuning Struggles with Forgetting in Machine Unlearning? Theoretical Insights and a Remedial Approach

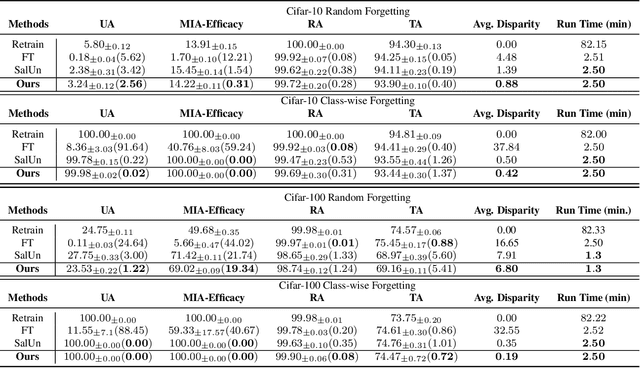
Machine Unlearning has emerged as a significant area of research, focusing on 'removing' specific subsets of data from a trained model. Fine-tuning (FT) methods have become one of the fundamental approaches for approximating unlearning, as they effectively retain model performance. However, it is consistently observed that naive FT methods struggle to forget the targeted data. In this paper, we present the first theoretical analysis of FT methods for machine unlearning within a linear regression framework, providing a deeper exploration of this phenomenon. We investigate two scenarios with distinct features and overlapping features. Our findings reveal that FT models can achieve zero remaining loss yet fail to forget the forgetting data, unlike golden models (trained from scratch without the forgetting data). This analysis reveals that naive FT methods struggle with forgetting because the pretrained model retains information about the forgetting data, and the fine-tuning process has no impact on this retained information. To address this issue, we first propose a theoretical approach to mitigate the retention of forgetting data in the pretrained model. Our analysis shows that removing the forgetting data's influence allows FT models to match the performance of the golden model. Building on this insight, we introduce a discriminative regularization term to practically reduce the unlearning loss gap between the fine-tuned model and the golden model. Our experiments on both synthetic and real-world datasets validate these theoretical insights and demonstrate the effectiveness of the proposed regularization method.

Imperative Learning: A Self-supervised Neural-Symbolic Learning Framework for Robot Autonomy

Data-driven methods such as reinforcement and imitation learning have achieved remarkable success in robot autonomy. However, their data-centric nature still hinders them from generalizing well to ever-changing environments. Moreover, collecting large datasets for robotic tasks is often impractical and expensive. To overcome these challenges, we introduce a new self-supervised neural-symbolic (NeSy) computational framework, imperative learning (IL), for robot autonomy, leveraging the generalization abilities of symbolic reasoning. The framework of IL consists of three primary components: a neural module, a reasoning engine, and a memory system. We formulate IL as a special bilevel optimization (BLO), which enables reciprocal learning over the three modules. This overcomes the label-intensive obstacles associated with data-driven approaches and takes advantage of symbolic reasoning concerning logical reasoning, physical principles, geometric analysis, etc. We discuss several optimization techniques for IL and verify their effectiveness in five distinct robot autonomy tasks including path planning, rule induction, optimal control, visual odometry, and multi-robot routing. Through various experiments, we show that IL can significantly enhance robot autonomy capabilities and we anticipate that it will catalyze further research across diverse domains.

On the Convergence of Multi-objective Optimization under Generalized Smoothness

Multi-objective optimization (MOO) is receiving more attention in various fields such as multi-task learning. Recent works provide some effective algorithms with theoretical analysis but they are limited by the standard $L$-smooth or bounded-gradient assumptions, which are typically unsatisfactory for neural networks, such as recurrent neural networks (RNNs) and transformers. In this paper, we study a more general and realistic class of $\ell$-smooth loss functions, where $\ell$ is a general non-decreasing function of gradient norm. We develop two novel single-loop algorithms for $\ell$-smooth MOO problems, Generalized Smooth Multi-objective Gradient descent (GSMGrad) and its stochastic variant, Stochastic Generalized Smooth Multi-objective Gradient descent (SGSMGrad), which approximate the conflict-avoidant (CA) direction that maximizes the minimum improvement among objectives. We provide a comprehensive convergence analysis of both algorithms and show that they converge to an $\epsilon$-accurate Pareto stationary point with a guaranteed $\epsilon$-level average CA distance (i.e., the gap between the updating direction and the CA direction) over all iterations, where totally $\mathcal{O}(\epsilon^{-2})$ and $\mathcal{O}(\epsilon^{-4})$ samples are needed for deterministic and stochastic settings, respectively. Our algorithms can also guarantee a tighter $\epsilon$-level CA distance in each iteration using more samples. Moreover, we propose a practical variant of GSMGrad named GSMGrad-FA using only constant-level time and space, while achieving the same performance guarantee as GSMGrad. Our experiments validate our theory and demonstrate the effectiveness of the proposed methods.

Understanding Forgetting in Continual Learning with Linear Regression

Continual learning, focused on sequentially learning multiple tasks, has gained significant attention recently. Despite the tremendous progress made in the past, the theoretical understanding, especially factors contributing to catastrophic forgetting, remains relatively unexplored. In this paper, we provide a general theoretical analysis of forgetting in the linear regression model via Stochastic Gradient Descent (SGD) applicable to both underparameterized and overparameterized regimes. Our theoretical framework reveals some interesting insights into the intricate relationship between task sequence and algorithmic parameters, an aspect not fully captured in previous studies due to their restrictive assumptions. Specifically, we demonstrate that, given a sufficiently large data size, the arrangement of tasks in a sequence, where tasks with larger eigenvalues in their population data covariance matrices are trained later, tends to result in increased forgetting. Additionally, our findings highlight that an appropriate choice of step size will help mitigate forgetting in both underparameterized and overparameterized settings. To validate our theoretical analysis, we conducted simulation experiments on both linear regression models and Deep Neural Networks (DNNs). Results from these simulations substantiate our theoretical findings.