Rejecting Outliers in 2D-3D Point Correspondences from 2D Forward-Looking Sonar Observations

Rejecting outliers before applying classical robust methods is a common approach to increase the success rate of estimation, particularly when the outlier ratio is extremely high (e.g. 90%). However, this method often relies on sensor- or task-specific characteristics, which may not be easily transferable across different scenarios. In this paper, we focus on the problem of rejecting 2D-3D point correspondence outliers from 2D forward-looking sonar (2D FLS) observations, which is one of the most popular perception device in the underwater field but has a significantly different imaging mechanism compared to widely used perspective cameras and LiDAR. We fully leverage the narrow field of view in the elevation of 2D FLS and develop two compatibility tests for different 3D point configurations: (1) In general cases, we design a pairwise length in-range test to filter out overly long or short edges formed from point sets; (2) In coplanar cases, we design a coplanarity test to check if any four correspondences are compatible under a coplanar setting. Both tests are integrated into outlier rejection pipelines, where they are followed by maximum clique searching to identify the largest consistent measurement set as inliers. Extensive simulations demonstrate that the proposed methods for general and coplanar cases perform effectively under outlier ratios of 80% and 90%, respectively.

Near-Optimal Sample Complexity for Iterated CVaR Reinforcement Learning with a Generative Model

In this work, we study the sample complexity problem of risk-sensitive Reinforcement Learning (RL) with a generative model, where we aim to maximize the Conditional Value at Risk (CVaR) with risk tolerance level $\tau$ at each step, named Iterated CVaR. %We consider the sample complexity of obtaining an $\epsilon$-optimal policy in an infinite horizon discounted MDP, given access to a generative model. % We first build a connection between Iterated CVaR RL with $(s, a)$-rectangular distributional robust RL with the specific uncertainty set for CVaR. We develop nearly matching upper and lower bounds on the sample complexity for this problem. Specifically, we first prove that a value iteration-based algorithm, ICVaR-VI, achieves an $\epsilon$-optimal policy with at most $\tilde{{O}}\left(\frac{SA}{(1-\gamma)^4\tau^2\epsilon^2}\right)$ samples, where $\gamma$ is the discount factor, and $S, A$ are the sizes of the state and action spaces. Furthermore, if $\tau \geq \gamma$, then the sample complexity can be further improved to $\tilde{{O}}\left( \frac{SA}{(1-\gamma)^3\epsilon^2} \right)$. We further show a minimax lower bound of ${\tilde{{O}}}\left(\frac{(1-\gamma \tau)SA}{(1-\gamma)^4\tau\epsilon^2}\right)$. For a constant risk level $0<\tau\leq 1$, our upper and lower bounds match with each other, demonstrating the tightness and optimality of our analyses. We also investigate a limiting case with a small risk level $\tau$, called Worst-Path RL, where the objective is to maximize the minimum possible cumulative reward. We develop matching upper and lower bounds of $\tilde{{O}}\left(\frac{SA}{p_{\min}}\right)$, where $p_{\min}$ denotes the minimum non-zero reaching probability of the transition kernel.

Scalable Bilevel Loss Balancing for Multi-Task Learning

Multi-task learning (MTL) has been widely adopted for its ability to simultaneously learn multiple tasks. While existing gradient manipulation methods often yield more balanced solutions than simple scalarization-based approaches, they typically incur a significant computational overhead of $\mathcal{O}(K)$ in both time and memory, where $K$ is the number of tasks. In this paper, we propose BiLB4MTL, a simple and scalable loss balancing approach for MTL, formulated from a novel bilevel optimization perspective. Our method incorporates three key components: (i) an initial loss normalization, (ii) a bilevel loss-balancing formulation, and (iii) a scalable first-order algorithm that requires only $\mathcal{O}(1)$ time and memory. Theoretically, we prove that BiLB4MTL guarantees convergence not only to a stationary point of the bilevel loss balancing problem but also to an $\epsilon$-accurate Pareto stationary point for all $K$ loss functions under mild conditions. Extensive experiments on diverse multi-task datasets demonstrate that BiLB4MTL achieves state-of-the-art performance in both accuracy and efficiency. Code is available at https://github.com/OptMN-Lab/-BiLB4MTL.

Independently-Normalized SGD for Generalized-Smooth Nonconvex Optimization

Recent studies have shown that many nonconvex machine learning problems meet a so-called generalized-smooth condition that extends beyond traditional smooth nonconvex optimization. However, the existing algorithms designed for generalized-smooth nonconvex optimization encounter significant limitations in both their design and convergence analysis. In this work, we first study deterministic generalized-smooth nonconvex optimization and analyze the convergence of normalized gradient descent under the generalized Polyak-Lojasiewicz condition. Our results provide a comprehensive understanding of the interplay between gradient normalization and function geometry. Then, for stochastic generalized-smooth nonconvex optimization, we propose an independently-normalized stochastic gradient descent algorithm, which leverages independent sampling, gradient normalization and clipping to achieve an $\mathcal{O}(\epsilon^{-4})$ sample complexity under relaxed assumptions. Experiments demonstrate the fast convergence of our algorithm.

Non-Asymptotic Analysis for Single-Loop Actor-Critic with Compatible Function Approximation

Actor-critic (AC) is a powerful method for learning an optimal policy in reinforcement learning, where the critic uses algorithms, e.g., temporal difference (TD) learning with function approximation, to evaluate the current policy and the actor updates the policy along an approximate gradient direction using information from the critic. This paper provides the \textit{tightest} non-asymptotic convergence bounds for both the AC and natural AC (NAC) algorithms. Specifically, existing studies show that AC converges to an $\epsilon+\varepsilon_{\text{critic}}$ neighborhood of stationary points with the best known sample complexity of $\mathcal{O}(\epsilon^{-2})$ (up to a log factor), and NAC converges to an $\epsilon+\varepsilon_{\text{critic}}+\sqrt{\varepsilon_{\text{actor}}}$ neighborhood of the global optimum with the best known sample complexity of $\mathcal{O}(\epsilon^{-3})$, where $\varepsilon_{\text{critic}}$ is the approximation error of the critic and $\varepsilon_{\text{actor}}$ is the approximation error induced by the insufficient expressive power of the parameterized policy class. This paper analyzes the convergence of both AC and NAC algorithms with compatible function approximation. Our analysis eliminates the term $\varepsilon_{\text{critic}}$ from the error bounds while still achieving the best known sample complexities. Moreover, we focus on the challenging single-loop setting with a single Markovian sample trajectory. Our major technical novelty lies in analyzing the stochastic bias due to policy-dependent and time-varying compatible function approximation in the critic, and handling the non-ergodicity of the MDP due to the single Markovian sample trajectory. Numerical results are also provided in the appendix.

On the Convergence of Multi-objective Optimization under Generalized Smoothness

Multi-objective optimization (MOO) is receiving more attention in various fields such as multi-task learning. Recent works provide some effective algorithms with theoretical analysis but they are limited by the standard $L$-smooth or bounded-gradient assumptions, which are typically unsatisfactory for neural networks, such as recurrent neural networks (RNNs) and transformers. In this paper, we study a more general and realistic class of $\ell$-smooth loss functions, where $\ell$ is a general non-decreasing function of gradient norm. We develop two novel single-loop algorithms for $\ell$-smooth MOO problems, Generalized Smooth Multi-objective Gradient descent (GSMGrad) and its stochastic variant, Stochastic Generalized Smooth Multi-objective Gradient descent (SGSMGrad), which approximate the conflict-avoidant (CA) direction that maximizes the minimum improvement among objectives. We provide a comprehensive convergence analysis of both algorithms and show that they converge to an $\epsilon$-accurate Pareto stationary point with a guaranteed $\epsilon$-level average CA distance (i.e., the gap between the updating direction and the CA direction) over all iterations, where totally $\mathcal{O}(\epsilon^{-2})$ and $\mathcal{O}(\epsilon^{-4})$ samples are needed for deterministic and stochastic settings, respectively. Our algorithms can also guarantee a tighter $\epsilon$-level CA distance in each iteration using more samples. Moreover, we propose a practical variant of GSMGrad named GSMGrad-FA using only constant-level time and space, while achieving the same performance guarantee as GSMGrad. Our experiments validate our theory and demonstrate the effectiveness of the proposed methods.

Finite-Time Analysis for Conflict-Avoidant Multi-Task Reinforcement Learning

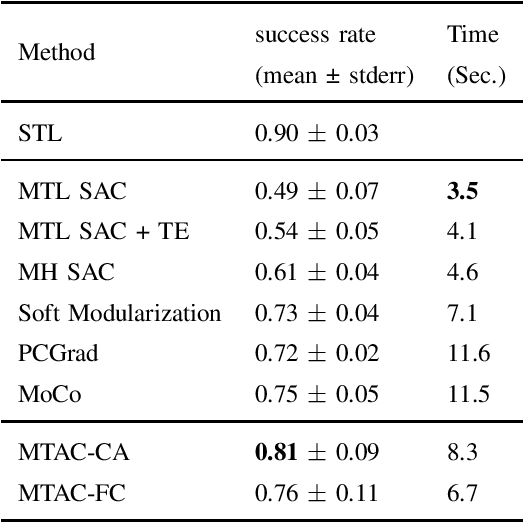
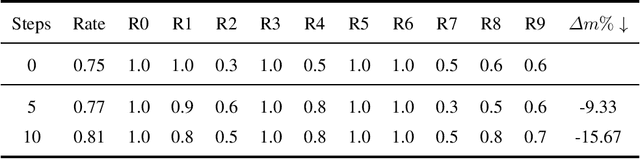
Multi-task reinforcement learning (MTRL) has shown great promise in many real-world applications. Existing MTRL algorithms often aim to learn a policy that optimizes individual objective functions simultaneously with a given prior preference (or weights) on different tasks. However, these methods often suffer from the issue of \textit{gradient conflict} such that the tasks with larger gradients dominate the update direction, resulting in a performance degeneration on other tasks. In this paper, we develop a novel dynamic weighting multi-task actor-critic algorithm (MTAC) under two options of sub-procedures named as CA and FC in task weight updates. MTAC-CA aims to find a conflict-avoidant (CA) update direction that maximizes the minimum value improvement among tasks, and MTAC-FC targets at a much faster convergence rate. We provide a comprehensive finite-time convergence analysis for both algorithms. We show that MTAC-CA can find a $\epsilon+\epsilon_{\text{app}}$-accurate Pareto stationary policy using $\mathcal{O}({\epsilon^{-5}})$ samples, while ensuring a small $\epsilon+\sqrt{\epsilon_{\text{app}}}$-level CA distance (defined as the distance to the CA direction), where $\epsilon_{\text{app}}$ is the function approximation error. The analysis also shows that MTAC-FC improves the sample complexity to $\mathcal{O}(\epsilon^{-3})$, but with a constant-level CA distance. Our experiments on MT10 demonstrate the improved performance of our algorithms over existing MTRL methods with fixed preference.

Constrained Reinforcement Learning Under Model Mismatch

Existing studies on constrained reinforcement learning (RL) may obtain a well-performing policy in the training environment. However, when deployed in a real environment, it may easily violate constraints that were originally satisfied during training because there might be model mismatch between the training and real environments. To address the above challenge, we formulate the problem as constrained RL under model uncertainty, where the goal is to learn a good policy that optimizes the reward and at the same time satisfy the constraint under model mismatch. We develop a Robust Constrained Policy Optimization (RCPO) algorithm, which is the first algorithm that applies to large/continuous state space and has theoretical guarantees on worst-case reward improvement and constraint violation at each iteration during the training. We demonstrate the effectiveness of our algorithm on a set of RL tasks with constraints.

Convergence Guarantees for RMSProp and Adam in Generalized-smooth Non-convex Optimization with Affine Noise Variance

This paper provides the first tight convergence analyses for RMSProp and Adam in non-convex optimization under the most relaxed assumptions of coordinate-wise generalized smoothness and affine noise variance. We first analyze RMSProp, which is a special case of Adam with adaptive learning rates but without first-order momentum. Specifically, to solve the challenges due to dependence among adaptive update, unbounded gradient estimate and Lipschitz constant, we demonstrate that the first-order term in the descent lemma converges and its denominator is upper bounded by a function of gradient norm. Based on this result, we show that RMSProp with proper hyperparameters converges to an $\epsilon$-stationary point with an iteration complexity of $\mathcal O(\epsilon^{-4})$. We then generalize our analysis to Adam, where the additional challenge is due to a mismatch between the gradient and first-order momentum. We develop a new upper bound on the first-order term in the descent lemma, which is also a function of the gradient norm. We show that Adam with proper hyperparameters converges to an $\epsilon$-stationary point with an iteration complexity of $\mathcal O(\epsilon^{-4})$. Our complexity results for both RMSProp and Adam match with the complexity lower bound established in \cite{arjevani2023lower}.

Large-Scale Non-convex Stochastic Constrained Distributionally Robust Optimization

Distributionally robust optimization (DRO) is a powerful framework for training robust models against data distribution shifts. This paper focuses on constrained DRO, which has an explicit characterization of the robustness level. Existing studies on constrained DRO mostly focus on convex loss function, and exclude the practical and challenging case with non-convex loss function, e.g., neural network. This paper develops a stochastic algorithm and its performance analysis for non-convex constrained DRO. The computational complexity of our stochastic algorithm at each iteration is independent of the overall dataset size, and thus is suitable for large-scale applications. We focus on the general Cressie-Read family divergence defined uncertainty set which includes $\chi^2$-divergences as a special case. We prove that our algorithm finds an $\epsilon$-stationary point with a computational complexity of $\mathcal O(\epsilon^{-3k_*-5})$, where $k_*$ is the parameter of the Cressie-Read divergence. The numerical results indicate that our method outperforms existing methods.} Our method also applies to the smoothed conditional value at risk (CVaR) DRO.