Large-Scale Non-convex Stochastic Constrained Distributionally Robust Optimization

Distributionally robust optimization (DRO) is a powerful framework for training robust models against data distribution shifts. This paper focuses on constrained DRO, which has an explicit characterization of the robustness level. Existing studies on constrained DRO mostly focus on convex loss function, and exclude the practical and challenging case with non-convex loss function, e.g., neural network. This paper develops a stochastic algorithm and its performance analysis for non-convex constrained DRO. The computational complexity of our stochastic algorithm at each iteration is independent of the overall dataset size, and thus is suitable for large-scale applications. We focus on the general Cressie-Read family divergence defined uncertainty set which includes $\chi^2$-divergences as a special case. We prove that our algorithm finds an $\epsilon$-stationary point with a computational complexity of $\mathcal O(\epsilon^{-3k_*-5})$, where $k_*$ is the parameter of the Cressie-Read divergence. The numerical results indicate that our method outperforms existing methods.} Our method also applies to the smoothed conditional value at risk (CVaR) DRO.

Robust Multimodal Learning with Missing Modalities via Parameter-Efficient Adaptation

Multimodal learning seeks to utilize data from multiple sources to improve the overall performance of downstream tasks. It is desirable for redundancies in the data to make multimodal systems robust to missing or corrupted observations in some correlated modalities. However, we observe that the performance of several existing multimodal networks significantly deteriorates if one or multiple modalities are absent at test time. To enable robustness to missing modalities, we propose simple and parameter-efficient adaptation procedures for pretrained multimodal networks. In particular, we exploit low-rank adaptation and modulation of intermediate features to compensate for the missing modalities. We demonstrate that such adaptation can partially bridge performance drop due to missing modalities and outperform independent, dedicated networks trained for the available modality combinations in some cases. The proposed adaptation requires extremely small number of parameters (e.g., fewer than 0.7% of the total parameters in most experiments). We conduct a series of experiments to highlight the robustness of our proposed method using diverse datasets for RGB-thermal and RGB-Depth semantic segmentation, multimodal material segmentation, and multimodal sentiment analysis tasks. Our proposed method demonstrates versatility across various tasks and datasets, and outperforms existing methods for robust multimodal learning with missing modalities.

Factorized Tensor Networks for Multi-Task and Multi-Domain Learning

Multi-task and multi-domain learning methods seek to learn multiple tasks/domains, jointly or one after another, using a single unified network. The key challenge and opportunity is to exploit shared information across tasks and domains to improve the efficiency of the unified network. The efficiency can be in terms of accuracy, storage cost, computation, or sample complexity. In this paper, we propose a factorized tensor network (FTN) that can achieve accuracy comparable to independent single-task/domain networks with a small number of additional parameters. FTN uses a frozen backbone network from a source model and incrementally adds task/domain-specific low-rank tensor factors to the shared frozen network. This approach can adapt to a large number of target domains and tasks without catastrophic forgetting. Furthermore, FTN requires a significantly smaller number of task-specific parameters compared to existing methods. We performed experiments on widely used multi-domain and multi-task datasets. We show the experiments on convolutional-based architecture with different backbones and on transformer-based architecture. We observed that FTN achieves similar accuracy as single-task/domain methods while using only a fraction of additional parameters per task.

Multimodal Transformer for Material Segmentation

Leveraging information across diverse modalities is known to enhance performance on multimodal segmentation tasks. However, effectively fusing information from different modalities remains challenging due to the unique characteristics of each modality. In this paper, we propose a novel fusion strategy that can effectively fuse information from different combinations of four different modalities: RGB, Angle of Linear Polarization (AoLP), Degree of Linear Polarization (DoLP) and Near-Infrared (NIR). We also propose a new model named Multi-Modal Segmentation Transformer (MMSFormer) that incorporates the proposed fusion strategy to perform multimodal material segmentation. MMSFormer achieves 52.05% mIoU outperforming the current state-of-the-art on Multimodal Material Segmentation (MCubeS) dataset. For instance, our method provides significant improvement in detecting gravel (+10.4%) and human (+9.1%) classes. Ablation studies show that different modules in the fusion block are crucial for overall model performance. Furthermore, our ablation studies also highlight the capacity of different input modalities to improve performance in the identification of different types of materials. The code and pretrained models will be made available at https://github.com/csiplab/MMSFormer.

Model-Free Robust Average-Reward Reinforcement Learning

Robust Markov decision processes (MDPs) address the challenge of model uncertainty by optimizing the worst-case performance over an uncertainty set of MDPs. In this paper, we focus on the robust average-reward MDPs under the model-free setting. We first theoretically characterize the structure of solutions to the robust average-reward Bellman equation, which is essential for our later convergence analysis. We then design two model-free algorithms, robust relative value iteration (RVI) TD and robust RVI Q-learning, and theoretically prove their convergence to the optimal solution. We provide several widely used uncertainty sets as examples, including those defined by the contamination model, total variation, Chi-squared divergence, Kullback-Leibler (KL) divergence and Wasserstein distance.

Robust Average-Reward Markov Decision Processes

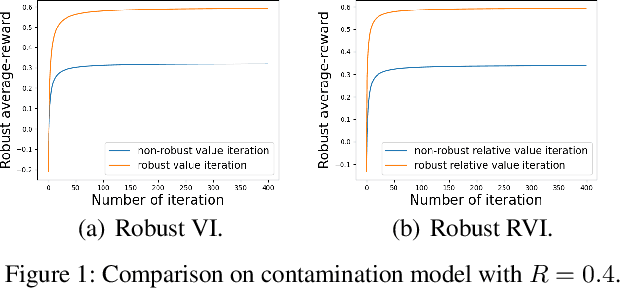
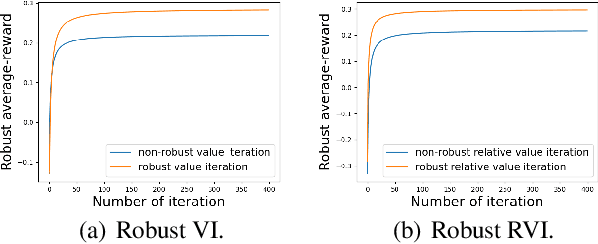
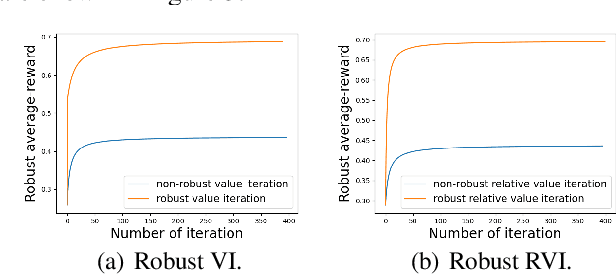
In robust Markov decision processes (MDPs), the uncertainty in the transition kernel is addressed by finding a policy that optimizes the worst-case performance over an uncertainty set of MDPs. While much of the literature has focused on discounted MDPs, robust average-reward MDPs remain largely unexplored. In this paper, we focus on robust average-reward MDPs, where the goal is to find a policy that optimizes the worst-case average reward over an uncertainty set. We first take an approach that approximates average-reward MDPs using discounted MDPs. We prove that the robust discounted value function converges to the robust average-reward as the discount factor $\gamma$ goes to $1$, and moreover, when $\gamma$ is large, any optimal policy of the robust discounted MDP is also an optimal policy of the robust average-reward. We further design a robust dynamic programming approach, and theoretically characterize its convergence to the optimum. Then, we investigate robust average-reward MDPs directly without using discounted MDPs as an intermediate step. We derive the robust Bellman equation for robust average-reward MDPs, prove that the optimal policy can be derived from its solution, and further design a robust relative value iteration algorithm that provably finds its solution, or equivalently, the optimal robust policy.

Incremental Task Learning with Incremental Rank Updates

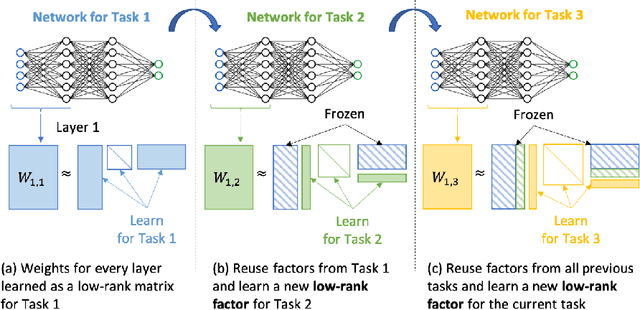
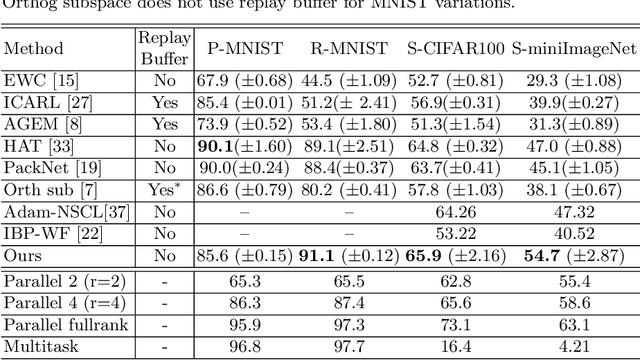
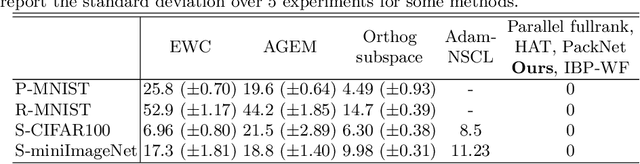
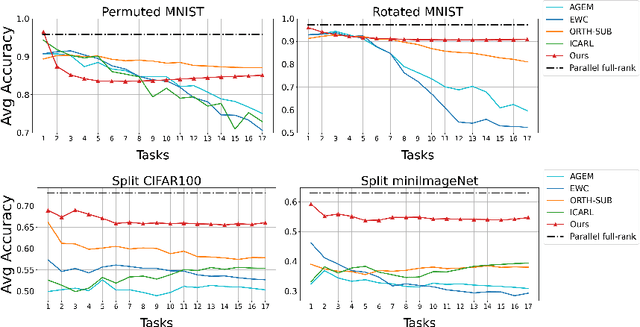
Incremental Task learning (ITL) is a category of continual learning that seeks to train a single network for multiple tasks (one after another), where training data for each task is only available during the training of that task. Neural networks tend to forget older tasks when they are trained for the newer tasks; this property is often known as catastrophic forgetting. To address this issue, ITL methods use episodic memory, parameter regularization, masking and pruning, or extensible network structures. In this paper, we propose a new incremental task learning framework based on low-rank factorization. In particular, we represent the network weights for each layer as a linear combination of several rank-1 matrices. To update the network for a new task, we learn a rank-1 (or low-rank) matrix and add that to the weights of every layer. We also introduce an additional selector vector that assigns different weights to the low-rank matrices learned for the previous tasks. We show that our approach performs better than the current state-of-the-art methods in terms of accuracy and forgetting. Our method also offers better memory efficiency compared to episodic memory- and mask-based approaches. Our code will be available at https://github.com/CSIPlab/task-increment-rank-update.git

Scaling and Scalability: Provable Nonconvex Low-Rank Tensor Estimation from Incomplete Measurements

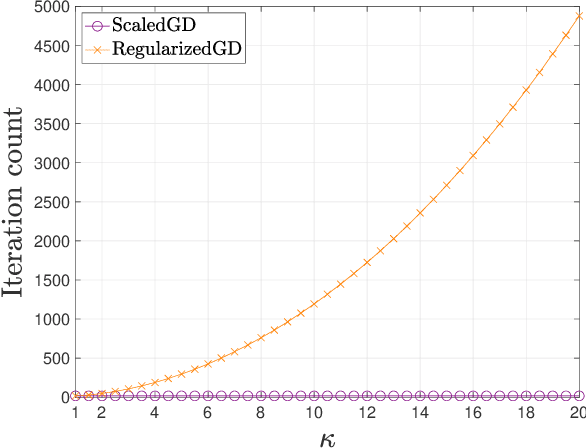
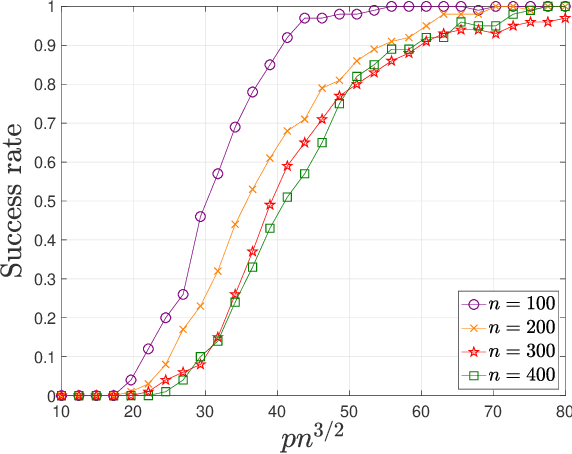
Tensors, which provide a powerful and flexible model for representing multi-attribute data and multi-way interactions, play an indispensable role in modern data science across various fields in science and engineering. A fundamental task is to faithfully recover the tensor from highly incomplete measurements in a statistically and computationally efficient manner. Harnessing the low-rank structure of tensors in the Tucker decomposition, this paper develops a scaled gradient descent (ScaledGD) algorithm to directly recover the tensor factors with tailored spectral initializations, and shows that it provably converges at a linear rate independent of the condition number of the ground truth tensor for two canonical problems -- tensor completion and tensor regression -- as soon as the sample size is above the order of $n^{3/2}$ ignoring other dependencies, where $n$ is the dimension of the tensor. This leads to an extremely scalable approach to low-rank tensor estimation compared with prior art, which suffers from at least one of the following drawbacks: extreme sensitivity to ill-conditioning, high per-iteration costs in terms of memory and computation, or poor sample complexity guarantees. To the best of our knowledge, ScaledGD is the first algorithm that achieves near-optimal statistical and computational complexities simultaneously for low-rank tensor completion with the Tucker decomposition. Our algorithm highlights the power of appropriate preconditioning in accelerating nonconvex statistical estimation, where the iteration-varying preconditioners promote desirable invariance properties of the trajectory with respect to the underlying symmetry in low-rank tensor factorization.