UniMamba: Unified Spatial-Channel Representation Learning with Group-Efficient Mamba for LiDAR-based 3D Object Detection

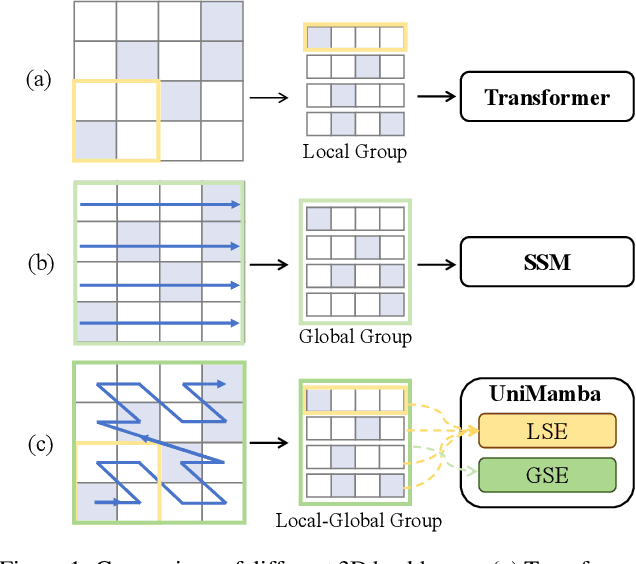
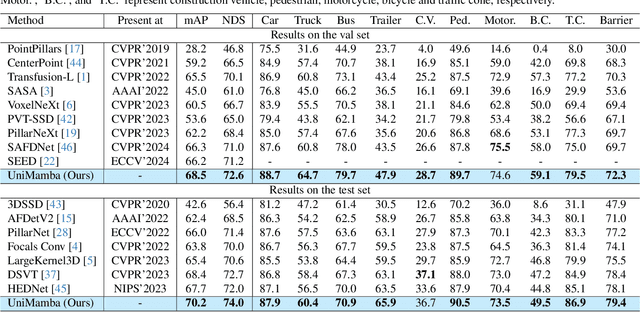
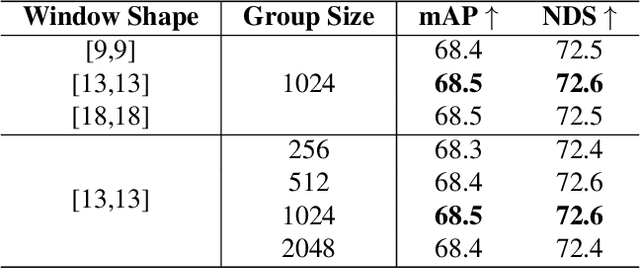
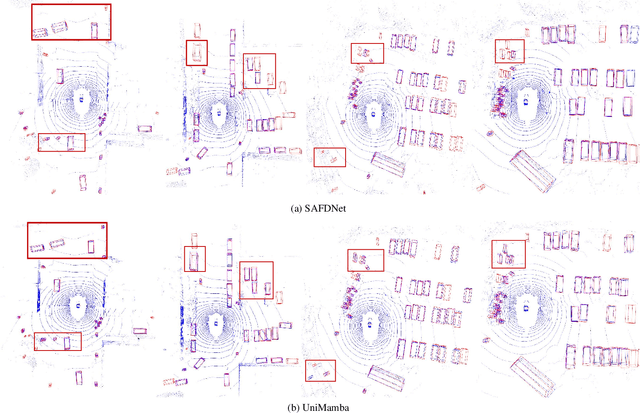
Recent advances in LiDAR 3D detection have demonstrated the effectiveness of Transformer-based frameworks in capturing the global dependencies from point cloud spaces, which serialize the 3D voxels into the flattened 1D sequence for iterative self-attention. However, the spatial structure of 3D voxels will be inevitably destroyed during the serialization process. Besides, due to the considerable number of 3D voxels and quadratic complexity of Transformers, multiple sequences are grouped before feeding to Transformers, leading to a limited receptive field. Inspired by the impressive performance of State Space Models (SSM) achieved in the field of 2D vision tasks, in this paper, we propose a novel Unified Mamba (UniMamba), which seamlessly integrates the merits of 3D convolution and SSM in a concise multi-head manner, aiming to perform "local and global" spatial context aggregation efficiently and simultaneously. Specifically, a UniMamba block is designed which mainly consists of spatial locality modeling, complementary Z-order serialization and local-global sequential aggregator. The spatial locality modeling module integrates 3D submanifold convolution to capture the dynamic spatial position embedding before serialization. Then the efficient Z-order curve is adopted for serialization both horizontally and vertically. Furthermore, the local-global sequential aggregator adopts the channel grouping strategy to efficiently encode both "local and global" spatial inter-dependencies using multi-head SSM. Additionally, an encoder-decoder architecture with stacked UniMamba blocks is formed to facilitate multi-scale spatial learning hierarchically. Extensive experiments are conducted on three popular datasets: nuScenes, Waymo and Argoverse 2. Particularly, our UniMamba achieves 70.2 mAP on the nuScenes dataset.

Auditing Differential Privacy in the Black-Box Setting

This paper introduces a novel theoretical framework for auditing differential privacy (DP) in a black-box setting. Leveraging the concept of $f$-differential privacy, we explicitly define type I and type II errors and propose an auditing mechanism based on conformal inference. Our approach robustly controls the type I error rate under minimal assumptions. Furthermore, we establish a fundamental impossibility result, demonstrating the inherent difficulty of simultaneously controlling both type I and type II errors without additional assumptions. Nevertheless, under a monotone likelihood ratio (MLR) assumption, our auditing mechanism effectively controls both errors. We also extend our method to construct valid confidence bands for the trade-off function in the finite-sample regime.

Estimating shared subspace with AJIVE: the power and limitation of multiple data matrices

Integrative data analysis often requires disentangling joint and individual variations across multiple datasets, a challenge commonly addressed by the Joint and Individual Variation Explained (JIVE) model. While numerous methods have been developed to estimate the shared subspace under JIVE, the theoretical understanding of their performance remains limited, particularly in the context of multiple matrices and varying levels of subspace misalignment. This paper bridges this gap by providing a systematic analysis of shared subspace estimation in multi-matrix settings. We focus on the Angle-based Joint and Individual Variation Explained (AJIVE) method, a two-stage spectral approach, and establish new performance guarantees that uncover its strengths and limitations. Specifically, we show that in high signal-to-noise ratio (SNR) regimes, AJIVE's estimation error decreases with the number of matrices, demonstrating the power of multi-matrix integration. Conversely, in low-SNR settings, AJIVE exhibits a non-diminishing error, highlighting fundamental limitations. To complement these results, we derive minimax lower bounds, showing that AJIVE achieves optimal rates in high-SNR regimes. Furthermore, we analyze an oracle-aided spectral estimator to demonstrate that the non-diminishing error in low-SNR scenarios is a fundamental barrier. Extensive numerical experiments corroborate our theoretical findings, providing insights into the interplay between SNR, matrix count, and subspace misalignment.

Trans-Glasso: A Transfer Learning Approach to Precision Matrix Estimation

Precision matrix estimation is essential in various fields, yet it is challenging when samples for the target study are limited. Transfer learning can enhance estimation accuracy by leveraging data from related source studies. We propose Trans-Glasso, a two-step transfer learning method for precision matrix estimation. First, we obtain initial estimators using a multi-task learning objective that captures shared and unique features across studies. Then, we refine these estimators through differential network estimation to adjust for structural differences between the target and source precision matrices. Under the assumption that most entries of the target precision matrix are shared with source matrices, we derive non-asymptotic error bounds and show that Trans-Glasso achieves minimax optimality under certain conditions. Extensive simulations demonstrate Trans Glasso's superior performance compared to baseline methods, particularly in small-sample settings. We further validate Trans-Glasso in applications to gene networks across brain tissues and protein networks for various cancer subtypes, showcasing its effectiveness in biological contexts. Additionally, we derive the minimax optimal rate for differential network estimation, representing the first such guarantee in this area.

Off-policy estimation with adaptively collected data: the power of online learning

We consider estimation of a linear functional of the treatment effect using adaptively collected data. This task finds a variety of applications including the off-policy evaluation (\textsf{OPE}) in contextual bandits, and estimation of the average treatment effect (\textsf{ATE}) in causal inference. While a certain class of augmented inverse propensity weighting (\textsf{AIPW}) estimators enjoys desirable asymptotic properties including the semi-parametric efficiency, much less is known about their non-asymptotic theory with adaptively collected data. To fill in the gap, we first establish generic upper bounds on the mean-squared error of the class of AIPW estimators that crucially depends on a sequentially weighted error between the treatment effect and its estimates. Motivated by this, we also propose a general reduction scheme that allows one to produce a sequence of estimates for the treatment effect via online learning to minimize the sequentially weighted estimation error. To illustrate this, we provide three concrete instantiations in (\romannumeral 1) the tabular case; (\romannumeral 2) the case of linear function approximation; and (\romannumeral 3) the case of general function approximation for the outcome model. We then provide a local minimax lower bound to show the instance-dependent optimality of the \textsf{AIPW} estimator using no-regret online learning algorithms.

RoboSense: Large-scale Dataset and Benchmark for Multi-sensor Low-speed Autonomous Driving

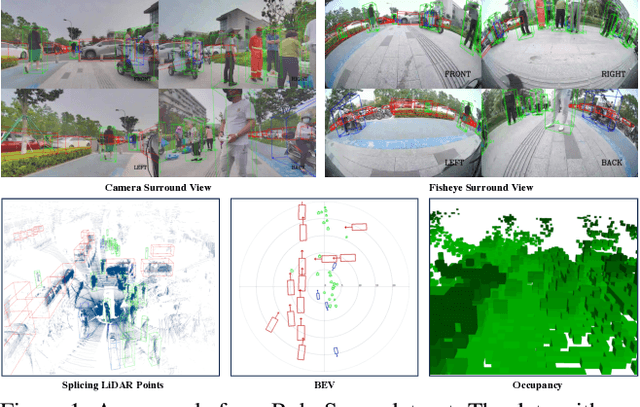
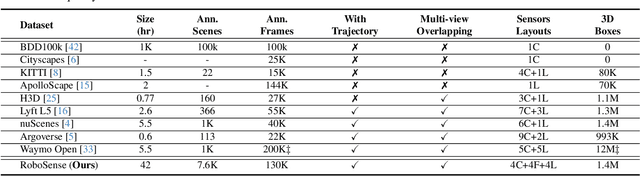
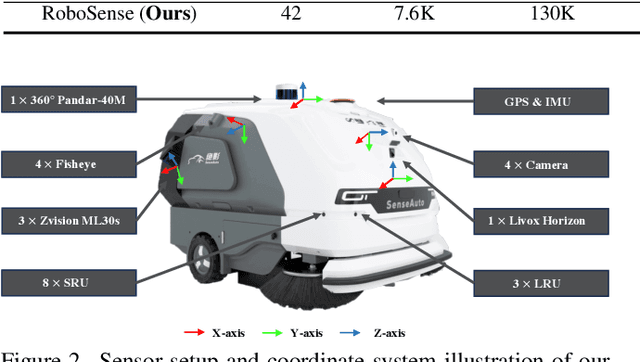
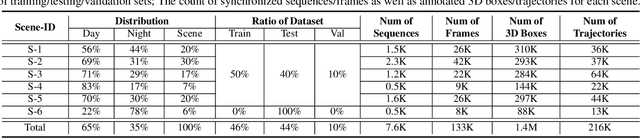
Robust object detection and tracking under arbitrary sight of view is challenging yet essential for the development of Autonomous Vehicle technology. With the growing demand of unmanned function vehicles, near-field scene understanding becomes an important research topic in the areas of low-speed autonomous driving. Due to the complexity of driving conditions and diversity of near obstacles such as blind spots and high occlusion, the perception capability of near-field environment is still inferior than its farther counterpart. To further enhance the intelligent ability of unmanned vehicles, in this paper, we construct a multimodal data collection platform based on 3 main types of sensors (Camera, LiDAR and Fisheye), which supports flexible sensor configurations to enable dynamic sight of view for ego vehicle, either global view or local view. Meanwhile, a large-scale multi-sensor dataset is built, named RoboSense, to facilitate near-field scene understanding. RoboSense contains more than 133K synchronized data with 1.4M 3D bounding box and IDs annotated in the full $360^{\circ}$ view, forming 216K trajectories across 7.6K temporal sequences. It has $270\times$ and $18\times$ as many annotations of near-field obstacles within 5$m$ as the previous single-vehicle datasets such as KITTI and nuScenes. Moreover, we define a novel matching criterion for near-field 3D perception and prediction metrics. Based on RoboSense, we formulate 6 popular tasks to facilitate the future development of related research, where the detailed data analysis as well as benchmarks are also provided accordingly.

LCSim: A Large-Scale Controllable Traffic Simulator

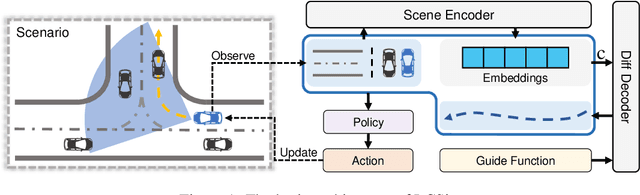
With the rapid development of urban transportation and the continuous advancement in autonomous vehicles, the demand for safely and efficiently testing autonomous driving and traffic optimization algorithms arises, which needs accurate modeling of large-scale urban traffic scenarios. Existing traffic simulation systems encounter two significant limitations. Firstly, they often rely on open-source datasets or manually crafted maps, constraining the scale of simulations. Secondly, vehicle models within these systems tend to be either oversimplified or lack controllability, compromising the authenticity and diversity of the simulations. In this paper, we propose LCSim, a large-scale controllable traffic simulator. LCSim provides map tools for constructing unified high-definition map (HD map) descriptions from open-source datasets including Waymo and Argoverse or publicly available data sources like OpenStreetMap to scale up the simulation scenarios. Also, we integrate diffusion-based traffic simulation into the simulator for realistic and controllable microscopic traffic flow modeling. By leveraging these features, LCSim provides realistic and diverse virtual traffic environments. Code and Demos are available at https://github.com/tsinghua-fib-lab/LCSim.

Random pairing MLE for estimation of item parameters in Rasch model

The Rasch model, a classical model in the item response theory, is widely used in psychometrics to model the relationship between individuals' latent traits and their binary responses on assessments or questionnaires. In this paper, we introduce a new likelihood-based estimator -- random pairing maximum likelihood estimator ($\mathsf{RP\text{-}MLE}$) and its bootstrapped variant multiple random pairing MLE ($\mathsf{MRP\text{-}MLE}$) that faithfully estimate the item parameters in the Rasch model. The new estimators have several appealing features compared to existing ones. First, both work for sparse observations, an increasingly important scenario in the big data era. Second, both estimators are provably minimax optimal in terms of finite sample $\ell_{\infty}$ estimation error. Lastly, $\mathsf{RP\text{-}MLE}$ admits precise distributional characterization that allows uncertainty quantification on the item parameters, e.g., construction of confidence intervals of the item parameters. The main idea underlying $\mathsf{RP\text{-}MLE}$ and $\mathsf{MRP\text{-}MLE}$ is to randomly pair user-item responses to form item-item comparisons. This is carefully designed to reduce the problem size while retaining statistical independence. We also provide empirical evidence of the efficacy of the two new estimators using both simulated and real data.

HoloVIC: Large-scale Dataset and Benchmark for Multi-Sensor Holographic Intersection and Vehicle-Infrastructure Cooperative

Vehicle-to-everything (V2X) is a popular topic in the field of Autonomous Driving in recent years. Vehicle-infrastructure cooperation (VIC) becomes one of the important research area. Due to the complexity of traffic conditions such as blind spots and occlusion, it greatly limits the perception capabilities of single-view roadside sensing systems. To further enhance the accuracy of roadside perception and provide better information to the vehicle side, in this paper, we constructed holographic intersections with various layouts to build a large-scale multi-sensor holographic vehicle-infrastructure cooperation dataset, called HoloVIC. Our dataset includes 3 different types of sensors (Camera, Lidar, Fisheye) and employs 4 sensor-layouts based on the different intersections. Each intersection is equipped with 6-18 sensors to capture synchronous data. While autonomous vehicles pass through these intersections for collecting VIC data. HoloVIC contains in total on 100k+ synchronous frames from different sensors. Additionally, we annotated 3D bounding boxes based on Camera, Fisheye, and Lidar. We also associate the IDs of the same objects across different devices and consecutive frames in sequence. Based on HoloVIC, we formulated four tasks to facilitate the development of related research. We also provide benchmarks for these tasks.

Batched Nonparametric Contextual Bandits

We study nonparametric contextual bandits under batch constraints, where the expected reward for each action is modeled as a smooth function of covariates, and the policy updates are made at the end of each batch of observations. We establish a minimax regret lower bound for this setting and propose Batched Successive Elimination with Dynamic Binning (BaSEDB) that achieves optimal regret (up to logarithmic factors). In essence, BaSEDB dynamically splits the covariate space into smaller bins, carefully aligning their widths with the batch size. We also show the suboptimality of static binning under batch constraints, highlighting the necessity of dynamic binning. Additionally, our results suggest that a nearly constant number of policy updates can attain optimal regret in the fully online setting.